特定の周波数だけを通過させるフィルタ

図1の(A)~(D)は多重帰還と呼ばれる形式を使用したフィルタ回路です.この中の1つは,1kHzの信号だけを通過させることを目的としたバンドパス・フィルタです.(A)~(D)の中でバンドパス・フィルタとして動作するのはどれでしょうか.
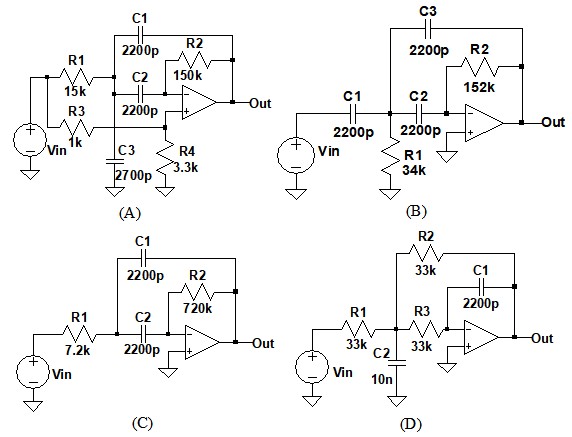
バンドパス・フィルタとして動作するのはどれ?
バンドパス・フィルタは,特定の周波数だけを通過させるフィルタです.図1の(A)~(D)の回路は,ローパス・フィルタ,ハイパス・フィルタ,ノッチ・フィルタ,バンドパス・フィルタとして動作します.入力信号周波数が高いとき,低いときに出力レベルがどうなるのかを考えれば,バンドパス・フィルタがどのフィルタに相当するのか分かります.
図1の(D)は高い周波数の信号が減衰するため,ローパス・フィルタとして動作します.(B)は,低い周波数の信号が減衰するためハイパス・フィルタです.(C)は,低域と高域が共に減衰するためバンドパス・フィルタとして動作します.(A)は,入力信号と逆位相のバンドパス出力が加算され,特定周波数が打ち消されるため,ノッチ・フィルタとなります.つまり,正解は(C)になります.
●多重帰還形フィルタのシミュレーション
まず,図1の(A)~(D)の回路がどのような周波数特性となるのか,シミュレーションしてみます.図2は,図1の多重帰還形フィルタの周波数特性をシミュレーションするための回路です.素子番号が重複しないよう,回路の素子名の末尾に(A)~(D)の文字を追加しています.そして,オクターブあたり100ポイントで100Hz~10kHzまでの周波数特性をシミュレーションします.
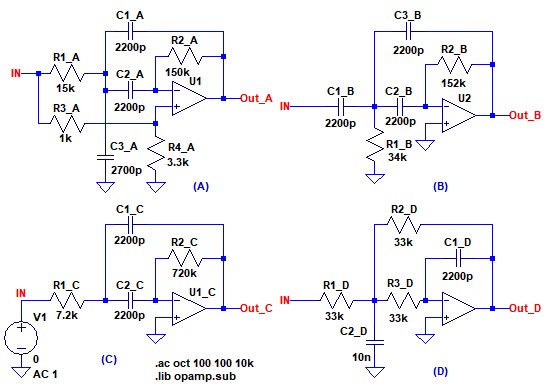
オクターブあたり100ポイントで100Hz~10kHzまでの周波数特性をシミュレーションする.
図3は,多重帰還形フィルタの周波数特性のシミュレーション結果です.回路(A)は,1kHzのゲインが最も小さいくなっており,ノッチ・フィルタとなっています.回路(B)は,1kHz以下のゲインが減衰しているためハイパス・フィルタです.回路(C)は,1KHzのゲインが最も大きく,バンドパス・フィルタとなっています.回路(D)は,1kHz以上のゲインが減衰しており,ローパス・フィルタとなっています.つまり,バンドパス・フィルタとして動作するのは回路(C)ということが分かります.
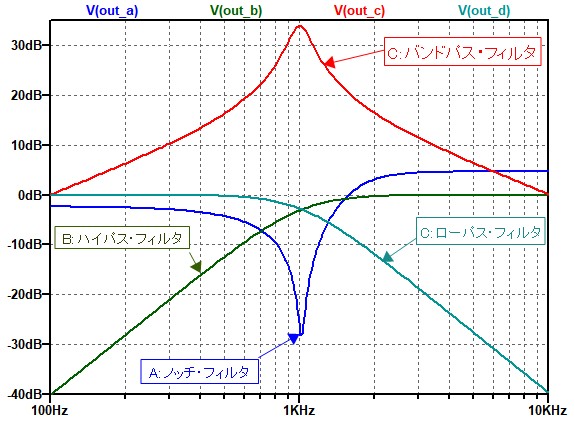
バンドパス・フィルタとして動作するのは回路Cということがわかる.
●多重帰還形バンドパス・フィルタの動作
図4は,多重帰還形バンドパス・フィルタ(回路C)の動作を解析するための回路図です.抵抗(R1)に流れる電流をiR1とし,コンデンサ(C1)に流れる電流をiC1,C2に流れる電流をiC2とします.
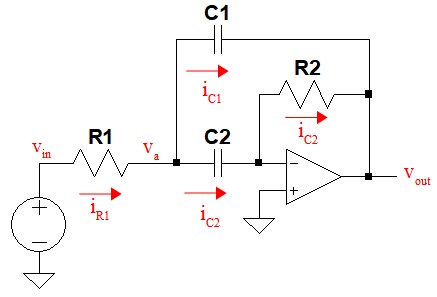
R1に流れる電流をiR1とし,C1に流れる電流をiC1,C2に流れる電流をiC2とする.
R1の電流はC1の電流とC2の電流を加算したものなので,式1になります.
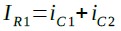 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また,iR1は式2になります.
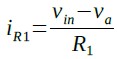 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
iC1は式3になります.
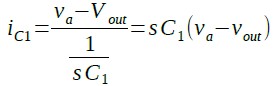 ・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・(3)
iC2は式4になります.
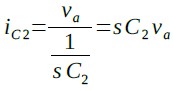 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式2~4を式1に代入すると式5が得られます.
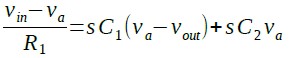 ・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・(5)
一方,OPアンプの帰還抵抗R2に流れる電流は,C2に流れる電流と同じiC2となるため,OPアンプの出力電圧(vout)は式6になります.
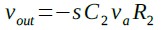 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式6及び式5からvoutを求めると式7のようになります.
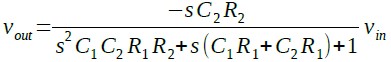 ・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・(7)
さらに,式7の分母,分子を「C1C2R1R2」で割ったものが式8です.
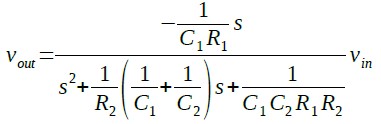 ・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・(8)
バンドパス・フィルタの一般的な伝達関数は式9で表されます.
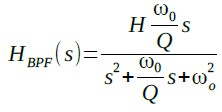 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
ω0がバンドパス・フィルタの中心周波数です.式9で「s=jω0」と置くと,式10のようにゲイン(G)は,Hになりなります.
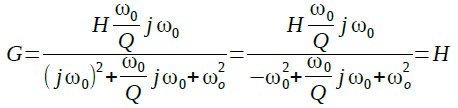 ・・・・・・・・・・・(10)
・・・・・・・・・・・(10)
つまりバンドパス・フィルタの中心周波数でのゲインはHとなることが分かります.式8と式9を比較し,ω0とQ及びHを計算するとω0は式11になります.
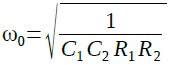 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
Qは,式12になります.
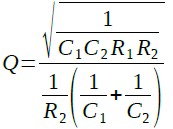 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
Hは,式13になります.
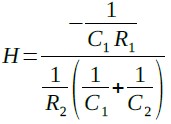 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
ここで「C1=C2=C」とすると,式12は式14に簡略化できます.
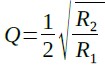 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
また,式13は式15のように簡略化できます.
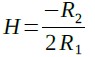 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
さらに,式16のようにRを定義すると,
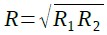 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
式11は,式17のように簡略化することができます.
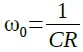 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
式16を使用して,式14を変形すると,R1は式18のように表すことができます.
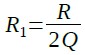 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)
また,R2は式19のように表すことができます.
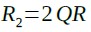 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(19)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(19)
式18と式19を式15に代入するとHは式20になり,Q2に比例することが分かります.
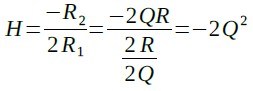 ・・・・・・・・・・・・・・・・・・・・・・・・・(20)
・・・・・・・・・・・・・・・・・・・・・・・・・(20)
●中心周波数1kHzのバンドパス・フィルタを設計する
ここからは,実際に中心周波数が1kHzのバンドパス・フィルタを設計していきます.バンドパス・フィルタを設計するためには,中心周波数だけではなく,Qをいくつにするかを決める必要があります.バンドパス・フィルタのQは,中心周波数とそれ以外の周波数のゲインのめりはりを表す係数です.Qが大きいほど中心周波数以外の成分が急峻に減衰します.中心周波数をf0とし,中心周波数のゲインに対してゲインが-3dBとなる周波数の幅をBとするとQは式21で表されます.
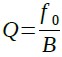 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(21)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(21)
今回は「f0=1kHz,Q=5」のフィルタを設計します.まず「C1=C2=C=2200pF」に決めます.そして,式17を使用して,式22のようにRを求めます.
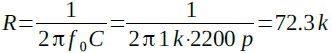 ・・・・・・・・・・・・・・・・・・・(22)
・・・・・・・・・・・・・・・・・・・(22)
次に,式22の結果と式18,式19からR1を求めると式23から約7.2kΩ
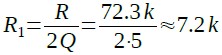 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(23)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(23)
同様にR2を求めると式24から約720kΩとなります.
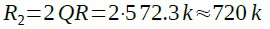 ・・・・・・・・・・・・・・・・・・・・・・・(24)
・・・・・・・・・・・・・・・・・・・・・・・(24)
また,中心周波数でのゲインは式25のように34dBになります.
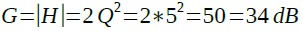 ・・・・・・・・・・・・・・・・・・・・・(25)
・・・・・・・・・・・・・・・・・・・・・(25)
●設計したバンドパス・フィルタのシミュレーション
図5がf0=1kHz,Q=5となるように定数を設定した多重帰還形バンドパス・フィルタの回路図です.
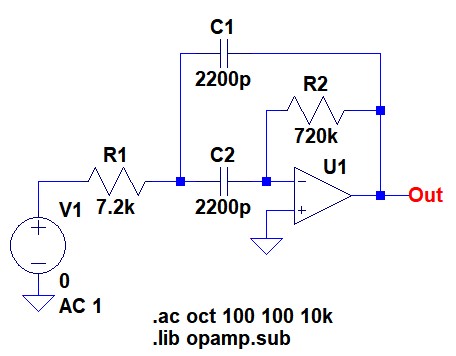
「f0=1kHz,Q=5」となるよう定数設定している.
図6がシミュレーション結果です.中心周波数のf0は1kHzで,そのときのゲインは34dBと設計通りになっています.
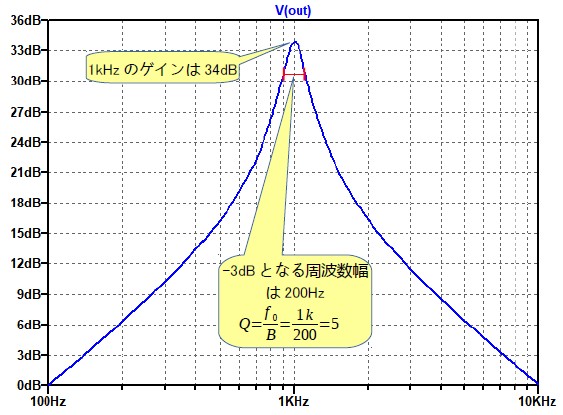
中心周波数及びゲインとQの値は設計値と同じ値になっている.
また,中心周波数から3dB減衰する周波数の幅は約200Hzとなっており,式26からQの値も設計値と同じ5になっていることが分かります.
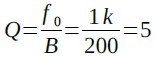 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(26)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(26)
●中心周波数のゲインを0dBにする
一般的に多重帰還形バンドパス・フィルタのゲインは式25のように0dB以上となり,Qを大きくするほどゲインも大きくなります.用途によっては中心周波数のゲインが0dBとなるように設定したい場合がありますが,その場合は抵抗(R1)を2つの抵抗に分割して分圧回路を構成します.
図7が分圧回路を追加し,中心周波数が0dBとなるように構成した多重帰還形バンドパス・フィルタです.
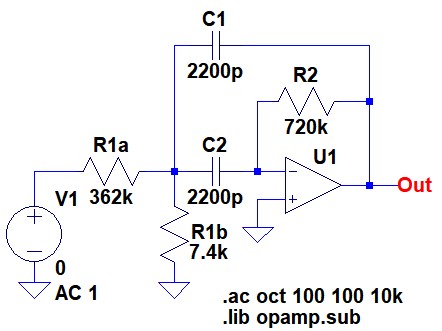
「f0=1kHz,Q=5,H=1(0dB)」となるよう定数設定している.
多重帰還形バンドパス・フィルタのゲインを0dBとするためにはR1aとR1bの分圧比とHを乗算した値が1になる必要があります.そのため,式27が成立するような値に選びます.
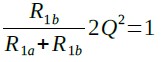 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(27)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(27)
また,R1aとR1bの並列抵抗値は式28のように式23の値と等しくする必要があります.
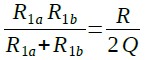 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(28)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(28)
式28と式27からR1aを求めると式29になり,今回の定数を代入すると362kΩになります.
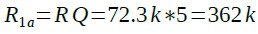 ・・・・・・・・・・・・・・・・・・・・・・・・(29)
・・・・・・・・・・・・・・・・・・・・・・・・(29)
さらに,式29と式28からR1bは式30になり,7.4kΩと計算できます.
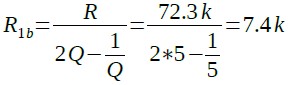 ・・・・・・・・・・・・・・・・・・・・・・(30)
・・・・・・・・・・・・・・・・・・・・・・(30)
図8は,図7のシミュレーション結果です.中心周波数の1kHzでのゲインは設計通り0dBとなっており,その他の特性は図6と同じです.
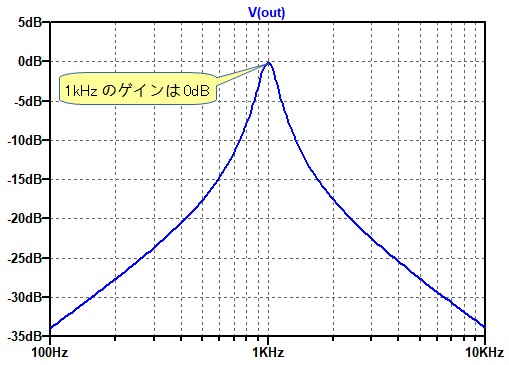
中心周波数の1kHzでのゲインは設計通り0dBとなっている.
以上,多重帰還形バンドパス・フィルタについて解説しました.中心周波数のゲインを0dBとする方法も紹介しましたが,その方法は一度信号を減衰させてから再度増幅することになるため,S/N比的には不利なことに注意が必要です.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_032.zip
●データ・ファイル内容
MFB_Filter.asc:図2の回路
BPF_1k.asc:図5の回路
BPF_1k_0dB.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










