TWIN-Tを使ったノッチ・フィルタ
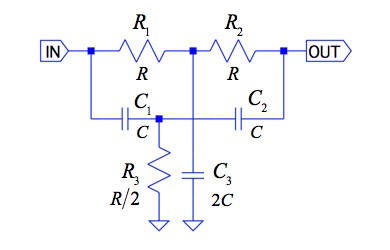
図1は，TWIN-Tと呼ばれる回路で，設定した1つの周波数でゲインが減衰するノッチ・フィルタとなります．3つの抵抗の関係は「R1=R2=R」，「R3=R/2」コンデンサの関係は「C1=C2=C」，「C3=2C」とします．図1のNull周波数(減衰が最大になる周波数)を1/10にするとき，ノッチ・フィルタのQ(減衰する谷の鋭さ)の変化として正しいのは，次の(1)～(4)のどれでしょうか．
(1) C1，C2，C3を10倍にするとQは大きくなる
(2) R1，R2，R3を10倍にするとQは大きくなる
(3) C1，C2，C3を2倍，R1，R2，R3を5倍にするとQは大きくなる
(4) R1=R2=R，R3=R/2，C1=C2=C，C3=2Cの関係であればQは変わらない
図1の入力から出力までの伝達関数は式1となります.
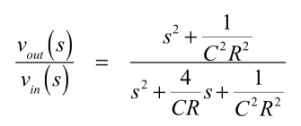・・・・・・・・・・・・・・・・・・・・・・(1)
また，ノッチ・フィルタの伝達関数は式2であり，式1と式2よりQが何で決まるか分かります．
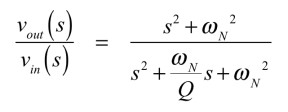・・・・・・・・・・・・・・・・・・・・・・・(2)
ノッチ・フィルタのQは，Null周波数の前後にあるゲインが-3dB(1/√2倍)となる2つの周波数差を帯域幅(BW)とし，Null周波数をfNとすれば，Qは「Q=fN/BW」となります．Qは減衰する谷の鋭さを表します．
式1と式2を比較し，Null周波数を求めると，式3となります．
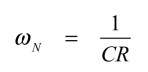・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
同様に，式1，式2より，Qに関係する方程式は式4となります．
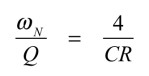・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
図1のQは式3と式4より式5となり，Null周波数に関係なくQは一定値になります．
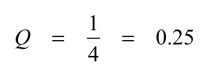・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
以上より，解答の(d)となります．
ノッチ・フィルタ(Notch filter)は，特定周波数の信号を除去する目的で使われるフィルタです．呼び名は複数あり，バンド・エリミネーション・フィルタ(BEF：Band Elimination Filter)，バンド・リジェクション・フィルタ(Band rejection filter)，バンドス・ストップ・フィルタ(Band stop filter)などです．
●TWIN-Tについて
TWIN-Tは，ノッチ・フィルタの1つで，T字の接続になっているLPF(Low Pass Filter)とHPF(High Pass Filter)を組み合わせた回路です．TWIN-Tの伝達関数は3次方程式です．しかし，フィルタは，1次と2次方程式を組み合わせて高次のフィルタの設計するため，3次方程式から2次方程式へ次数を下げています．この次数を下げる1つの方法として，3つの抵抗の関係を「R1=R2=R」，「R3=R/2」，コンデンサの関係を「C1=C2=C」，「C3=2C」としています．図1を詳しく書くと図2となり，左右対称となるため，対称型TWIN-Tと呼びます．解答で述べたように，対称型TWIN-TのQは一定となり調整ができません．
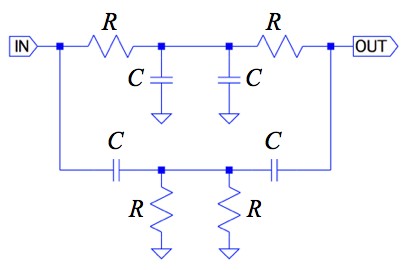
GND間にある抵抗とコンデンサを1つにまとめると図1となる．
●TWIN-TのQをシミュレーションで確かめる
図3は，対称型TWIN-TのQが一定値であるかを確かめる回路です．回路は，図3(a)～図3(d)の4つあります．
図3(a)は「R1=R2=16kΩ」，「R3=16kΩ/2」，「C1=C2=0.01μF」，「C3=2×0.01μF」としNull周波数が1kHzの定数です．
図3(b)は，図3(a)のコンデンサを10倍にし，Null周波数を100Hzにした回路です．
図3(c)は，図3(a)の抵抗を10倍にし，Null周波数を100Hzにした回路です．
図3(d)は，図3(a)のコンデンサを2倍，抵抗を5倍にし，Null周波数を100Hzにした回路です．
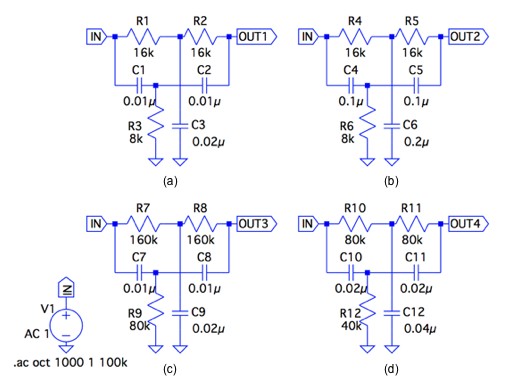
(a) fN=1kHz (b) Cを10倍へ変更しfN=100Hz (c) Rを10倍へ変更しfN=100Hz (b) Cを2倍，Rを5倍へ変更しfN=100Hz．
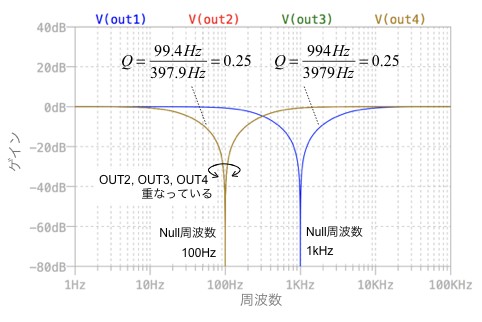
図4は，図3のシミュレーション結果です．帯域幅は，Null周波数を境にして，その前後にある-3dBの帯域幅とNull周波数より計算しました．図4より，Qの値は変化せず一定であることが分かり，その値は式5で計算した値となります．
●Q調整ができるノッチ・フィルタ
図5のノッチ・フィルタは，ブート・ストラップを使い，対称型TWIN-Tへ出力の一部を正帰還することにより，Qを調整することができます．Qの調整は赤枠で示した可変抵抗でおこない，シミュレーションでは変数nを調整します．対称型TWIN-Tですので，3つの抵抗と3つのコンデンサの関係は，図1と同じにします．
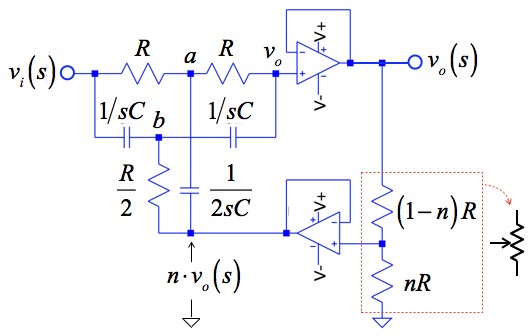
対称型TWIN-Tへ出力信号の一部を正帰還している．
ここでは，図5の対称型TWIN-T周辺の回路方程式をたててノッチ・フィルタの伝達関数を求めます．またその伝達関数よりNull周波数とQを求めます．
a点のKCLは，式6となります．
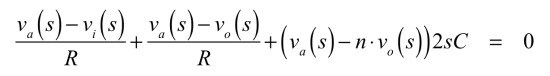・・・・・(6)
式6を整理して式7となります．
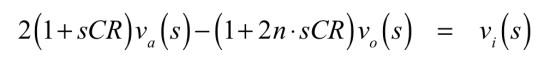・・・・・(7)
b点のKCLは，式8となります．
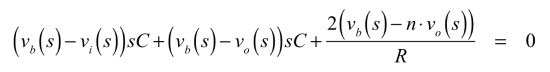・・・・・(8)
式8を整理して式9となります．
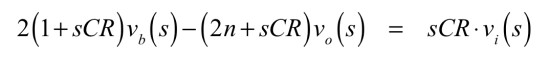・・・・・(9)
OPアンプ非反転端子のKCLは式10となります．
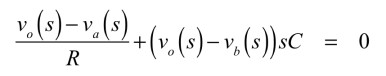・・・・・・・・・・・・・・・・(10)
式10を整理して式11となります．
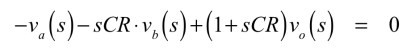・・・・・・・・・・・・・・(11)
式7，式9，式11を使い，クラメルの公式(連立一次方程式と行列式の関係)を用いて，vo(s)を求めると，式12となります．
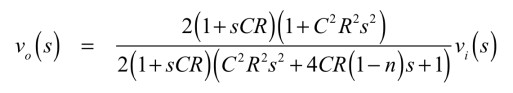・・・・・・・(12)
式12からも分かるようにTWIN-Tは，3次の伝達関数になります．図5は，図1と同じように対称型TWIN-Tの3つの抵抗と3つのコンデンサの関係としたので，分子と分母にある「2(1+sCR)」の項で打ち消しあい，次数を下げた2次の伝達関数となります．式2と比較するため，式12を変形すると式13となります．
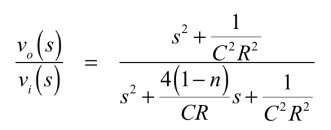・・・・・・・・・・・・・・・・・・・(13)
式13と式2の各項を比較すると，Null周波数は式14となります．
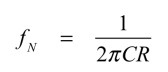・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
同様に，Qは式15となります．
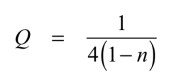・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
このように，Null周波数は抵抗とコンデンサで決まり，Qは変数nで独立に調整できることが分かります．
●Q調整できるノッチ・フィルタのシミュレーション
図6は，図5のAC解析をする回路で，Null周波数が50Hzのノッチ・フィルタです．回路定数の決め方ですが，一般にコンデンサは，抵抗に比べて選べる値が少ないので，入手しやすい値を選びます．次に式14を使い，選んだコンデンサとNull周波数より抵抗を選びます．抵抗も入手しやすい値がありますので，この検討を複数回繰り返しながら最良となる組み合わせを探します．信号源抵抗の影響を受けないようにするには，TWIN-Tの抵抗値は信号源抵抗の100倍以上を目安にします．OPアンプは，入力バイアス電流や入力インピーダンスの影響を抑えるため，JFET入力のOPアンプを使いました．
以上の検討を繰り返し，図6の対称型TWIN-Tの回路定数は「R1=R2=31.6kΩ」，「R3=31.6kΩ/2」，「C1=C2=0.1μF」，「C3=2×0.1μF」としました．Qの調整は変数nを「.stepコマンド」で0.1，0.7，0.9と与え，3回シミュレーションします．
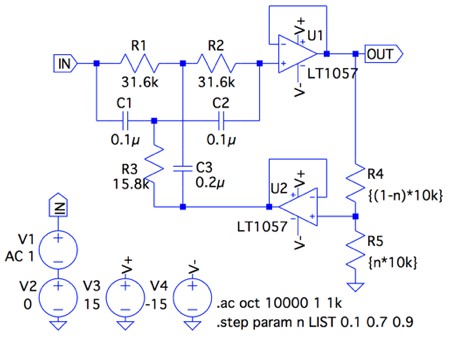
nを調整したときQの変化を調べる．
図7は，図6のシミュレーション結果です．ノッチ・フィルタのNull周波数が50Hz，Qが変数nで独立に調整できる様子が分かります．TWIN-Tへ出力の一部を正帰還するため，nが大きくなるとNull周波数での減衰が小さくなります．Null周波数付近を拡大して確認してください．
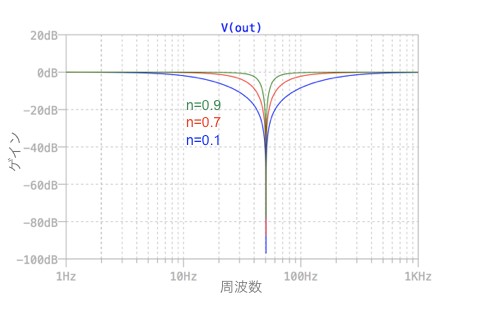
nを調整すると，Qが変わる様子がわかる．
図8は，図6の回路を使い，周波数1kHz，振幅1Vの正弦波へ，周波数50Hz，振幅0.1Vが重畳した波形を入力したとき，出力信号が50Hzを除去する様子をシミュレーションしました．図6からの変更点は，過渡解析の指定を「.tran 200m」，V1を「SINE(0 1 1k)」，V2を「SINE(0 0.1 50)」としています．
図8の上段がIN端子の波形，下段がOUT端子の波形で「n=0.7」のときをプロットしました．上段の波形は，大きなうねりが50Hzで，細かな振動が1kHzです．下段の出力波形をみると，大きなうねりが抑圧され，1kHzの信号が現れています．このようにOUT端子の波形は50Hzが除去されていることが分かります．
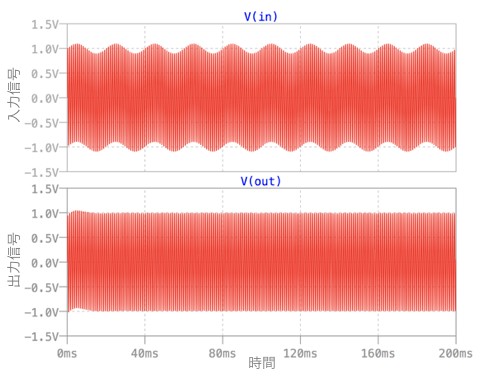
入力信号は，周波数1kHz，振幅1Vの正弦波へ，周波数50Hz，振幅0.1Vが重畳したもの．
出力信号は50Hzを除去した波形となる．
以上，解説したように， 対称型TWIN-TのQは一定値ですが，ブート・ストラップを使うと，Null周波数に関係なく独立にQの調整ができます．Q調整が必要ないときは，ブート・ストラップをかけるOPアンプと可変抵抗を取り去り，対称型TWIN-Tの出力をボルテージ・ホロワ回路で出力するようにすれば良いことになります．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_031.zip
●データ・ファイル内容
TWIN-T.asc：図3の回路
Q_Adjustable_Notch_filter.asc：図6の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源＆アナログ回路入門・アーカイブs
(7) IoT時代のLTspiceアナログ回路入門アーカイブs
