チェビシェフ型ローパス・フィルタ

■問題
アナログ回路の基礎 ― 中級

小川　敦　Atsushi Ogawa

　図1は，ローパス・フィルタの要求特性に合わせて設計された，チェビシェフ型ローパス・フィルタの周波数特性をグラフ化したものです．(A)～(D)は，チェビシェフ型ローパス・フィルタの説明文ですが，間違っている説明文があります．間違っている説明文はどれでしょうか．

図1　チェビシェフ型ローパス・フィルタの周波数特性

(A)　チェビシェフ型ローパス・フィルタは，バタワース型ローパス・フィルタよりもカットオフ周波数近傍の減衰特性を急峻にできる．

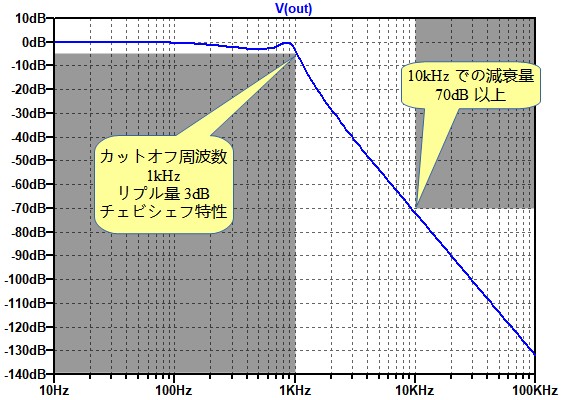
(B)　チェビシェフ型ローパス・フィルタは，リプル（通過帯域内でゲインの変動）を大きくするほど，カットオフ周波数近傍の減衰特性を急峻にできる．

(C)　OPアンプでフィルタを構成する場合，チェビシェフ型ローパス・フィルタは，同じ次数のバタワース型ローパス・フィルタよりも少ない部品点数で構成できる．

(D)　チェビシェフ型ローパス・フィルタのカットオフ周波数での減衰量は，3dBになるとは限らない．

■ヒント

　チェビシェフ型フィルタはロシアの数学者チェビシェフが発見したチェビシェフ多項式をフィルタに応用したものです．バタワース型フィルタとは異なった性質を持っており，(A)～(D)の中の3つはその性質を正しく説明しています．素直に考えれば，どれが誤った説明か分かると思います．

■解答

　チェビシェフ型ローパス・フィルタとバタワース型ローパス・フィルタの伝達関数は，同じ次数であれば同じ形で表されます．異なっているのは係数だけです．そのため，OPアンプでフィルタを構成する場合，回路構成は全く同じで，抵抗とコンデンサの値だけが異なったものになります．したがって，チェビシェフ型ローパス・フィルタの部品点数が少ないというのは誤った説明です．

■解説

●チェビシェフ特性の減衰量
　n次のチェビシェフ型ローパス・フィルタの伝達関数の絶対値は式1で表されます．ここで，ω_cがカットオフ周波数，εがリプル係数，Tn()がn次のチェビシェフ多項式です．

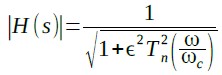・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　バターワース特性とは異なり，通過帯域内でゲインの変動（リプル）が発生します．また，カットオフ周波数近傍の減衰特性の傾きが，バターワース特性よりも急峻になります．リプル(r)の大きさはリプル係数(ε)で決まり，dBで表したその大きさは式2で表されます．

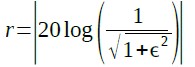・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　リプルのデシベル値からリプル係数を求めるには式2を変形した式3を使用します．

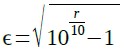・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　リプルを大きくすると減衰特性の傾きが急峻になり，要求される減衰量を得るために必要な次数が少なくなります．「バターワース型ローパス・フィルタ ―― IoT時代のLTspiceアナログ回路入門 028」で，バターワース型ローパス・フィルタのカットオフ周波数での減衰量は3dBでした．しかし，チェビシェフ型ローパスフィルタのカットオフ周波数での減衰量は3dBとは限りません．奇数次のチェビシェフ型ローパスフィルタの場合，カットオフ周波数での減衰量は，リプルの値と同じ減衰量となります．偶数次のチェビシェフ型ローパスフィルタのカットオフ周波数での減衰量は，直流利得と同じ値(0dB)になります．リプル量を「r」，カットオフ周波数を「ω_c」とし，周波数(ω_s)で要求される減衰量を「A」としたときに必要なフィルタの次数は，式4で計算することができます．

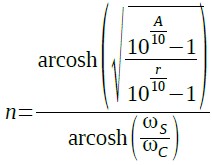・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　一例として「r=3dB，ω_c=1kHz，ω_s=10kHz，A=70dB」とすると，式5のように「n=2.92」となり，3次のフィルタでよいことが分かります．同じ条件でバターワース型ローパス・フィルタの場合，必要な次数を計算すると4次のフィルタが必要となります．チェビシェフ型ローパス・フィルタのほうがより少ない次数で必要な減衰量を確保できることになります．

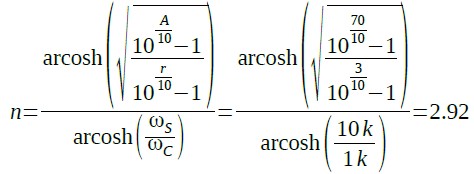・・・・・・・・・・(5)

●チェビシェフ特性とバタワース特性の伝達関数
　チェビシェフ型ローパス・フィルタの伝達関数も，バタワース型ローパス・フィルタとまったく同じ形式で表すことができます．バタワース型ローパス・フィルタでは次数を決めれば，その伝達関数の係数は一意に決まりました．しかし，チェビシェフ型ローパス・フィルタは，リプル量をいくつにするかで，係数が変化します．この係数は計算により求めることができます．フィルタ関係の書籍にはリプル量ごとに各次数の係数が記載されていますので，それを利用するほうが手軽です．式6は，リプル量を3dBとした3次チェビシェフ型ローパス・フィルタの伝達関数です．ここでω_cはカットオフ周波数です．

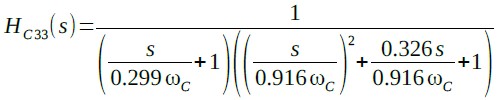・・・・・・・・・(6)

　式7は，比較のための3次バタワース型ローパス・フィルタの伝達関数です．

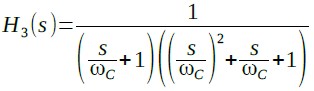・・・・・・・・・・・・・・・・・・・・・(7)

　図2は，この2つの伝達関数の周波数特性をシミュレーションするための回路です．E₃が式6で，E₁が式7となります．

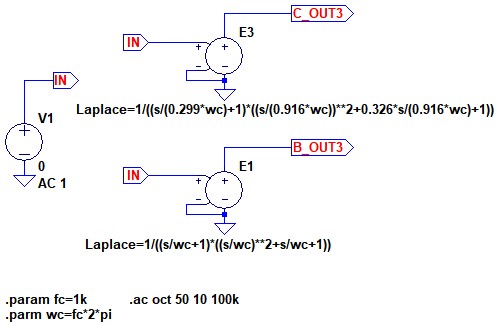
図2　電圧制御電圧源で伝達関数の周波数特性をシミュレーションする回路
チェビシェフ型とバタワース型ローパス・フィルタの特性を比較する．

　図3は，2つの伝達関数の周波数特性のシミュレーション結果です．チェビシェフ型ローパス・フィルタは，通過帯域内でゲインの変動（リプル）が発生しています．しかし，10kHzでの減衰量はバタワース型よりも大きくなっています．

図3　2つの伝達関数の周波数特性のシミュレーション結果
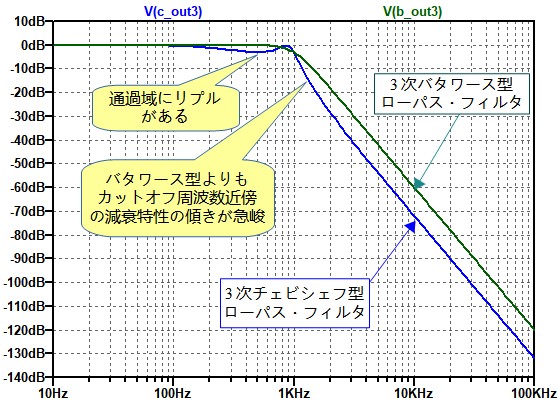
10kHzでの減衰量はチェビシェフ型ローパス・フィルタのほうが大きい．

●リプル量を変えたときのチェビシェフ特性のシミュレーション
　次に，チェビシェフ型ローパス・フィルタのリプル量のを変えたときの周波数特性をシミュレーションします．式8は3次チェビシェフ型ローパス・フィルタでリプル量を1dBとしたときの伝達関数です．

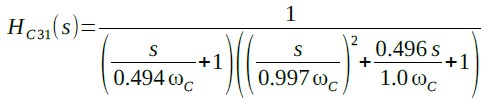・・・・・・・・・(8)

　式9はリプル量2dBのときの伝達関数です．

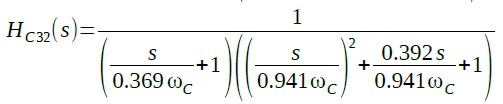・・・・・・・・(9)

　図4は，チェビシェフ型ローパス・フィルタのリプル量を変えた伝達関数の周波数特性をシミュレーションするための回路です．E₁が1dB，E₂が2dB，E₃が3dBとなるようにリプル量を設定し，伝達関数はE₁が式6，E₂が式8，E₃が式9となります．

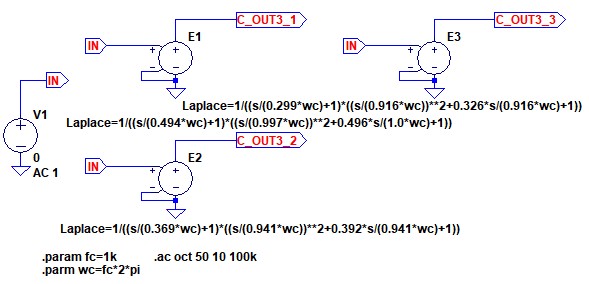
図4　リプル量を変えた伝達関数の周波数特性をシミュレーションするための回路
リプル量を1dB，2dB，3dBとなるように係数を設定している．

　図5がリプル量を変えた，3次チェビシェフ型ローパス・フィルタの伝達関数のシミュレーション結果です．拡大図を見ると，カットオフ周波数(1kHz)での減衰量はリプルの大きさと同じ値になっていることが分かります．また，カットオフ周波数近傍の減衰量の傾きは，リプルが大きい方が急峻になっています．

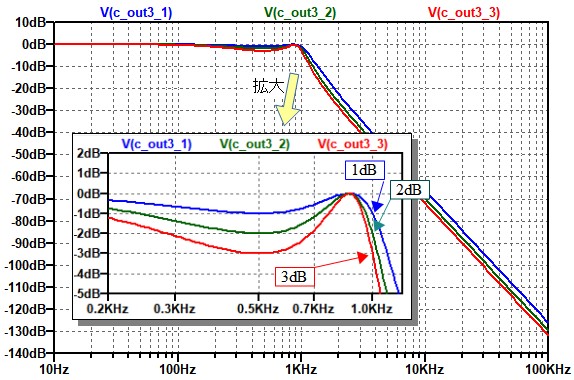
図5　リプル量を変えた，チェビシェフ型ローパス・フィルタのシミュレーション結果
カットオフ周波数(1kHz)での減衰量はリプルの大きさと同じ．

●次数を変えたときのチェビシェフ特性のリプル
　チェビシェフ特性のリプルは，次数が偶数か奇数かによって振る舞いが異なります．そこで，同じリプル量(3dB)と同じカットオフ周波数(1kHz)で次数を変えたチェビシェフ型ローパス・フィルタの特性をシミュレーションしてみます．式10が4次のチェビシェフ型ローパス・フィルタの伝達関数です．

・・・・・(10)

　式11が5次の伝達関数です．

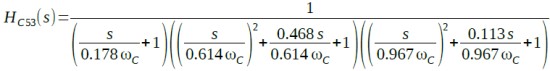・・・・・(11)

　式12が6次の伝達関数です．

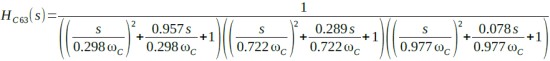・・・・・(12)

　図6は，3次(式6)，4次(式10)，5次(式11)，6次(式12)のフィルタのリプル特性を比較する伝達関数をシミュレーションするための回路図です．E₁が3次，E₂が4次，E₃が5次，E₄が6次となっています．

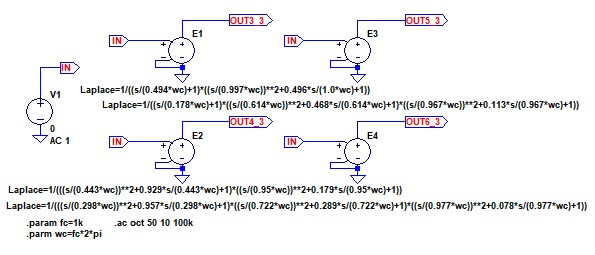
図6　次数を変えたチェビシェフ型ローパス・フィルタの特性をシミュレーションする回路
3次，4次，5次，6次のフィルタのリプル特性を比較する．

　図7は，図6のシミュレーション結果で，3次，4次，5次，6次のチェビシェフ型ローパス・フィルタの周波数特性となります．次数が偶数のとき，通過帯域内でゲインが増加する方向でリプルが発生しています．また，次数が奇数のとき，ゲインが減少する方向のリプルが発生しています．

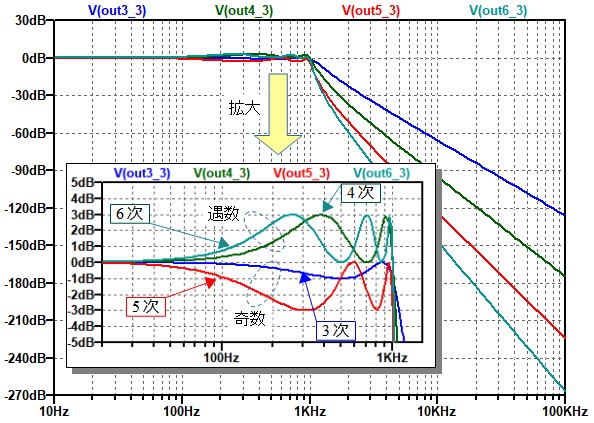
図7　3次，4次，5次，6次のチェビシェフ型ローパス・フィルタの周波数特性
次数が偶数のときは通過域でゲイン増加し，奇数のときは減少する．

●OPアンプを使用したチェビシェフ型ローパス・フィルタを設計する
　式10の伝達関数をOPアンプを使用して構成する方法は，まず，式10を式13と式14のように2つに分解します．

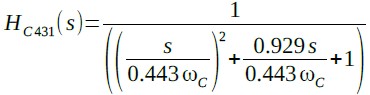・・・・・・・・・・・・・・・・・(13)

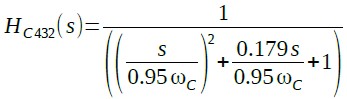・・・・・・・・・・・・・・・・・・(14)

　ここで、ω_cの係数をkとし，一次の項の係数（式13の0.929s，式14の0.179s）の逆数をQとして，式13と式14を一般式であらわすと，式15になります．

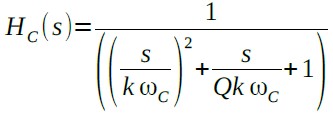・・・・・・・・・・・・・・・・・・・(15)

　式13のQ₁は1/0.929，式14のQ₂は1/0.179です．kは，式13のk1が0.443で，式14のk2が0.95す．この伝達関数を実現するため，図8のようなサレンキー型フィルタを使用します．

図8　サレンキー型ローパス・フィルタ
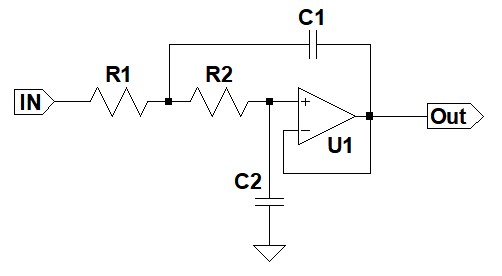
2次ローパスフィルタの回路形式として一般的に使われるもの．

　この回路の伝達関数は式16のようになります．なので，式13と式14を式16で構成すれば，式10の伝達関数を実現できます．

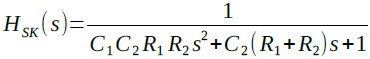・・・・・・・・・・・・・・・・・(16)

　式15の特性を図8の回路で実現するためには，式15の特性と式16の特性が同じになるようにする必要があります．まず，分母のS²の項に着目すると式17が成立すればよいことになります．

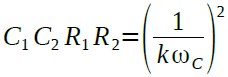・・・・・・・・・・・・・・・・・・・・・・・・・・(17)

　式17からkω_cを求めると式18になります．

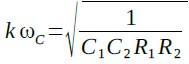・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)

　次に，sの項に着目すると式19が成立すればよいことになります．

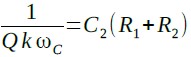・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(19)

　式15を式13，式14と同じ特性になるようにするには，式13と式14が，式18と式19を満たすように，C₁，C₂，R₁，R₂の定数を設定すれば良いことになります．計算を簡単にするために「R₁=R₂=R」とすると，式18が式20に変形できます．

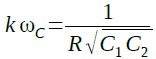・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(20)

　式19は式21のように変形できます．

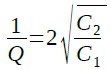・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(21)

　ここで，C₁を入手しやすい定数で決め打ちし10nFとします，そして，式22よりQ₁からC₂を求めると式22のように2.2nFになります．

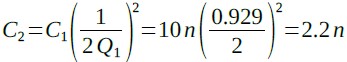・・・・・・・・・・・・・・・・・・(22)

　抵抗(R)は，式23のように77kΩと求められます．

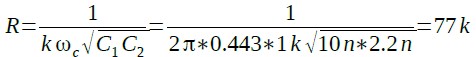・・・・・・・・・・(23)

　また，同様にQ₂からC₂とRを求めると式24からC₂が80pFとなります．

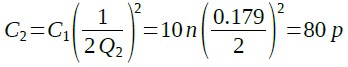・・・・・・・・・・・・・・・・・・(24)

　また，式25からRは，187kΩになります．

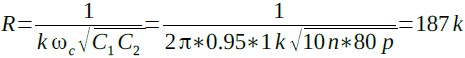・・・・・・・・・・(25)

●OPアンプを使用したチェビシェフ型ローパス・フィルタ
　図9が式22～式25で計算した定数を使用したチェビシェフ型ローパス・フィルタです．回路構成は，バターワース型ローパス・フィルタとまったく同じで，抵抗・コンデンサの定数が異なっているだけです．

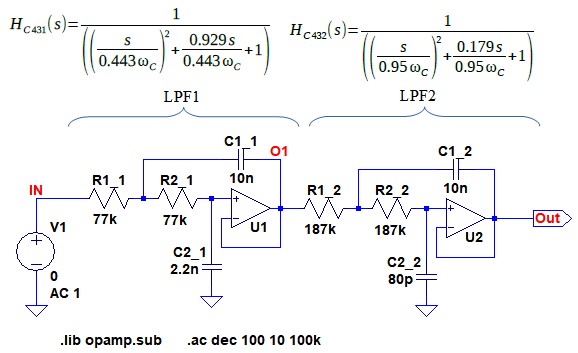
図9　OPアンプを使用して構成したチェビシェフ型ローパス・フィルタ
回路構成は，バターワース型ローパス・フィルタと同じで定数のみが異なる．

　図10は，図9のシミュレーション結果です．青線が式13の伝達関数となる，2次のサレンキー・ローパス・フィルタ(LPF1)の周波数特性です．そして緑線が式14の伝達関数となる，2次のサレンキー・ローパス・フィルタ(LPF2)の周波数特性です．LPF2のQが高いため，1kHz前後でゲインがかなり上昇しています．このLPF1とLPF2の特性を合成したものが，赤線の4次のチェビシェフ型ローパス・フィルタです．

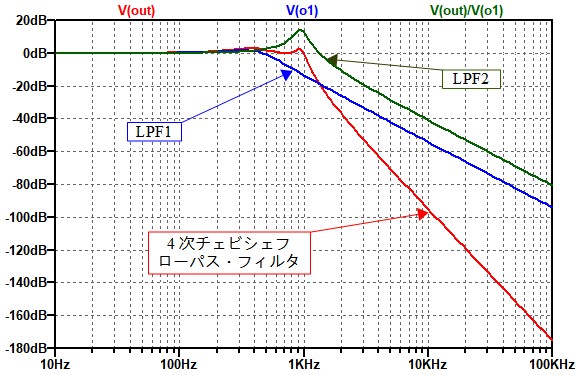
図10　OPアンプを使用して構成したチェビシェフ型ローパス・フィルタ
LPF1とLPF2の特性を合成したものが4次のチェビシェフ型ローパス・フィルタ．

　以上，チェビシェフ型ローパス・フィルタについて解説しました．チェビシェフ型フィルタはバタワース型フィルタよりも減衰特性を急峻にできますが，通過域内のリプルがどの程度許容できるかを十分検討する必要があります．また，チェビシェフ型ハイパス・フィルタに関しても，図9の回路のコンデンサと抵抗を入れ替え，定数を変更することで実現することができます．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_030.zip

●データ・ファイル内容
Chebyshev_Butterworth_LPF.asc：図2の回路
Chebyshev_LPF_rpl.asc：図4の回路
Chebyshev_LPF.asc：図6の回路
OPamp_Chebyshev_LPF.asc：図9の回路