バターワース型ローパス・フィルタ

図1は,ローパス・フィルタの要求特性とその要求特性に合わせて設計されたローパス・フィルタの周波数特性をグラフ化したものです.ローパス・フィルタの要求特性は「通過域のゲインが0dB,カットオフ周波数が1kHzでバターワース特性,10kHzでの減衰量が70dB以上」というものです.この要求特性を満たす,最も次数の少ないバターワース型ローパス・フィルタを設計しました.その次数は次の(A)~(D)のどれでしょうか.
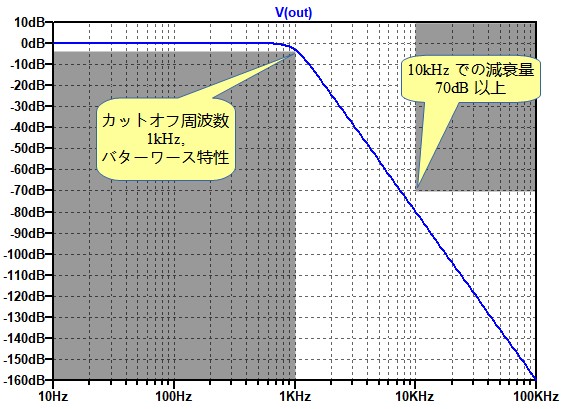
要求特性を満たす,最も少ない次数は?
バターワース特性は,通過域の周波数特性がフラットで,減衰特性の傾きはフィルタの次数に比例します.n次のバターワース型ローパス・フィルタの減衰特性の傾きが何dB/decadeかを考えれば答えが分かります.
n次のバターワース型フィルタの減衰特性の傾きはn*20db/decadeとなります.つまり,カットオフ周波数が1kHzのバターワース型ローパス・フィルタの10kHzでの減衰量はn*20dBとなります.「n=3」のときの減衰量が60dBで,「n=4」のときの減衰量が80dBなので,減衰量が70dB以上で最も少ない次数は4次ということになります.
●バターワース特性の減衰量
n次のバターワース型ローパス・フィルタの伝達関数の絶対値は,式1で表されます.ここでωcはカットオフ周波数です.
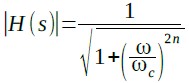 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
このフィルタの減衰量をデシベルで表したものをAとすると,Aは式2となります.
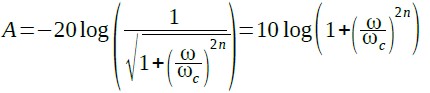 ・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・(2)
(ω/ωc)2n>>1とみなせる場合,式2は式3のように簡略化できます.
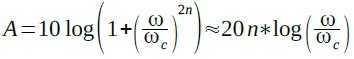 ・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・(3)
式3より,減衰特性の傾きは(20*n)dB/decadeとなることが分かります.つまり,周波数が10倍になるごとに減衰量は20*n [dB]ずつ増加することになります.減衰量(A)からnを求めるには式3を式4のように変形します.
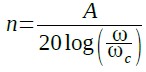 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4を使用することで,要求減衰特性から,設計するフィルタの次数を計算することができます.図1の条件を代入すると式5のようにnは3.5となるので,切り上げて「n=4」となり,4次のフィルタとすればよいことが分かります.
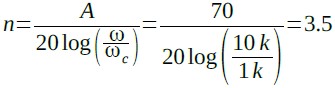 ・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・(5)
●バターワース特性の伝達関数
絶対値が式1で表されるようなバターワース特性の伝達関数は,フィルター関係の書籍に係数とともに掲載されています.ウィキペディアにも正規化バターワース多項式[表1(1)*]として掲載されており,3次の場合は式6のようになります.

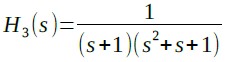 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
カットオフ周波数をωcとしたい場合はsをωcで割り式7のように変形します.
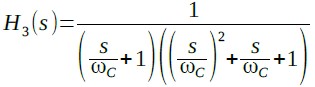 ・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・(7)
同様に4次の伝達関数は式8,
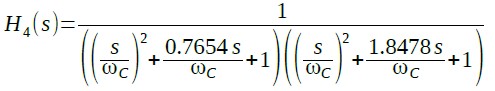 ・・・・・・・・・(8)
・・・・・・・・・(8)
5次の伝達関数は式9,
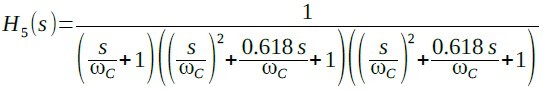 ・・・・・・(9)
・・・・・・(9)
6次の伝達関数は式10になります.
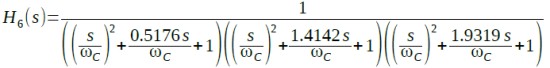 ・・・・・(10)
・・・・・(10)
LTspiceの電圧制御電圧源には,このような伝達関数を直接記述して周波数特性を確認する機能があります.図2が3次から6次までのバターワース型ローパス・フィルタの伝達関数をシミュレーションするための回路図です.fcという変数にカットオフ周波数を入力します.図1では1kHzに設定していますが,この部分を書き換えることで,いろいろなカットオフ周波数のフィルタとすることができます.
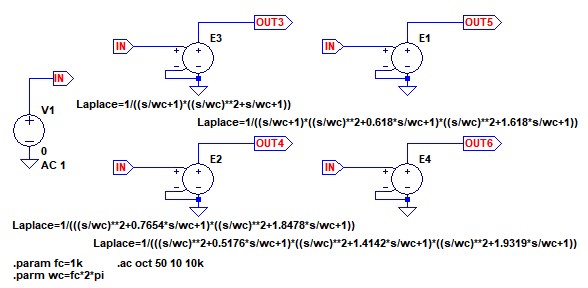
fcという変数の値を変えれば,フィルタのカットオフ周波数を変更できる.
図3がバターワース型ローパス・フィルタの伝達関数のシュミレーション結果です.いずれの曲線も3dB減衰するカットオフ周波数は1kHzとなっており,10kHzでの減衰量はそれぞれ60dB,80dB,100dB,120dBとなっています.このグラフからも,10kHzでの減衰量を70dB以上とするには4次のバターワース型フィルタとすればよいことが分かります.
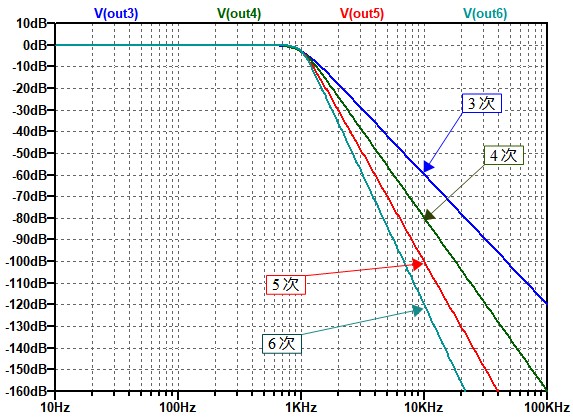
10kHzでの減衰量はそれぞれ60dB,80dB,100dB,120dBとなっている.
●OPアンプを使用したバターワース型ローパス・フィルタを設計する
式8のような伝達関数になる回路を設計すれば,4次のバターワース型ローパス・フィルタとすることができます.このような回路を実現する場合,一般的には1次や2次の特性のものを縦続接続します.次数の大きなものを一括して設計するのは非常に煩雑になるためです.そこで,式8を式11と式12のように2つに分解します.
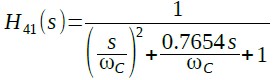 ・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・(11)
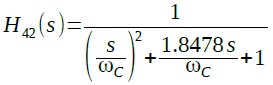 ・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・(12)
式11と式12の違いは,1次の項の係数だけです.この係数の逆数は一般的にQという記号で表します.そこで,それぞれのQを「Q1=1/0.7653,Q2=1/1.8478」とします.このような2次特性の伝達関数を実現する回路には色々なものがありますが,ここでは2次ローパスフィルタの回路形式として代表的なサレンキー型フィルタを使用します(図4).
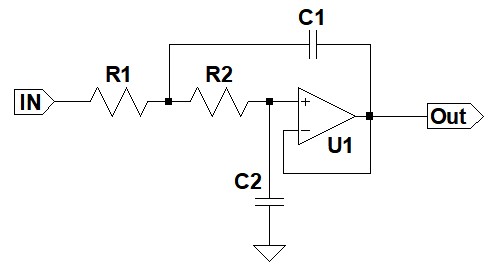
2次ローパスフィルタの回路形式として一般的に使われるもの.
この回路の伝達関数は式13になります.
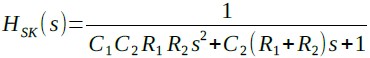 ・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・(13)
式13を式11,式12と同じ特性になるようにするためには,式14と式15を満たすように定数を設定すれば良いことになります.
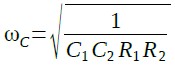 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
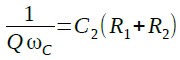 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
計算を簡単にするために「R1=R2=R」とすると,式14は,式16
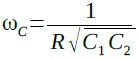 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
式15は,式17のように変形できます.
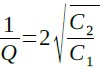 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
ここでC1を10nFとし,式17よりQ1からC2を求めると式18のように1.5nFになります.
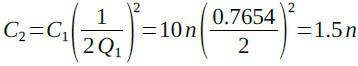 ・・・・・・・・・・・・・・・・・・(18)
・・・・・・・・・・・・・・・・・・(18)
抵抗Rは式19のように41kΩと求められます.
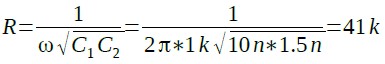 ・・・・・・・・・・・・・・・・(19)
・・・・・・・・・・・・・・・・(19)
また,同様にQ2からC2を求めると式20の8.5nF
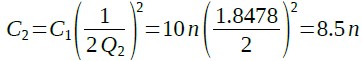 ・・・・・・・・・・・・・・・・・(20)
・・・・・・・・・・・・・・・・・(20)
Rを求めると式21の17.3kΩになります.
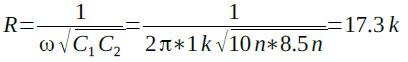 ・・・・・・・・・・・・・・(21)
・・・・・・・・・・・・・・(21)
●OPアンプを使用したバターワース型ローパス・フィルタの確認
図5が式18~式21で計算した定数を使用したバターワース型ローパス・フィルタです.式11の伝達関数のほうが式12よりもQが大きく,振幅が大きくなるため,式11の伝達関数となるサレンキー・フィルター(LPF2)を後段に配置しています.
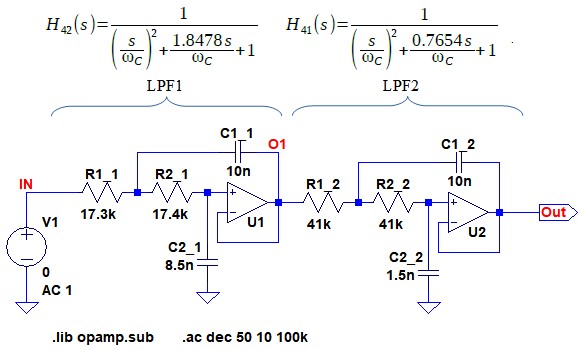
Qの大きいサレンキー・フィルターを後段に配置している.
図6は,図5のバターワース型ローパス・フィルタのシミュレーション結果です.青線が式12の伝達関数となる,2次のサレンキー・ローパス・フィルタ(LPF1)の周波数特性です.そして緑線が式11の伝達関数となる,2次のサレンキー・ローパス・フィルタ(LPF2)の周波数特性です.LPF2のほうがQが高いため,1kHz前後でゲインが上昇しています.このLPF1とLPF2の特性を合成したものが,赤線の4次のバターワース型ローパス・フィルタです.これは,図3の4次のフィルターの特性とまったく同じ特性になっています.
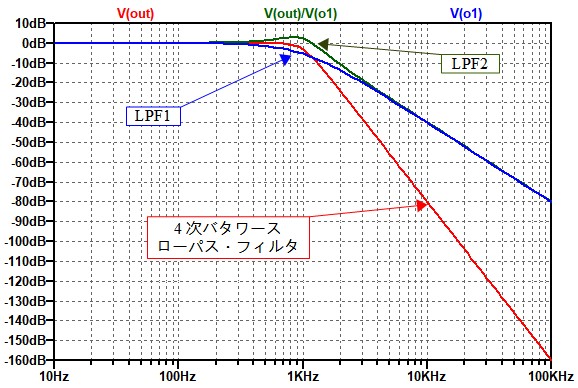
LPF1とLPF2の特性を合成したものが4次のバターワース型ローパス・フィルタ.
以上,バターワース型ローパス・フィルタについて解説しました.ハイパス・フィルタに関しても,図5の回路のコンデンサと抵抗を入れ替え,定数を変更することで実現することができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_028.zip
●データ・ファイル内容
Butterworth_LPF.asc:図3の回路
OPamp_Butterworth_LPF.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










