容量を大きく見せるブートストラップ回路

図1(a)は,OPアンプ(U1)と抵抗(R1,R2,R3),コンデンサ(C1)を使い,C1の容量が大きくみえる長時定数回路(Long Time Constant Circuit)です.図1(b)は,図1(a)のブートストラップを使った,容量マルチプライヤ回路を等価容量(Ceq)と等価抵抗(Req)を直列に接続した等価回路です.
図1(a)の回路を,図1(b)の等価回路で表したとき,CeqとReqを表す式は,次の(a)~(d)のどれでしょうか.なお,OPアンプは理想とします.
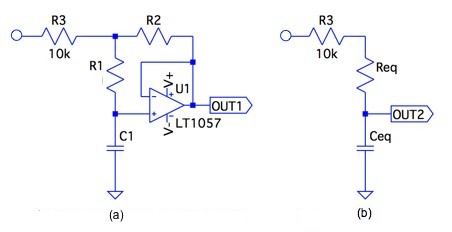
C1の容量が大きくみえる.
(b)Ceq=(1+R1/R2)C1,Req=R2
(c)Ceq=(1+R2/R1)C1,Req=R1||R2
(d)Ceq=(1+R2/R1)C1,Req=R2
図1(a)のR3から右側をみたインピーダンスをR1,R2,C1で表し,図1(b)のR3から右側をみたインピーダンと比較することにより,ReqとCeqの関係を求めることができます.
図1(a)のR3から右側をみたインピーダンスは式1となります.
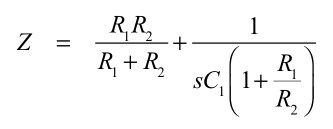 ・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・(1)
図1(b)のR3から右側をみたインピーダンスは式2となります.
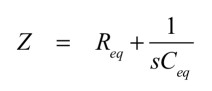 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式1の右辺第一項は,R1とR2の並列抵抗です.右辺第二項のコンデンサは,C1を回路のゲイン「1+R1/R2」で乗じた値です.よって式1と式2を比較すると,ReqとCeqは式3の関係となり,(a)となります.
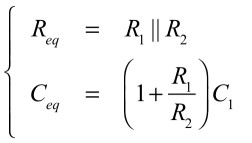 ・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・(3)
●見掛け上コンデンサの容量が大きくなった回路
コンデンサの容量を大きくみせる回路技法の1つに,ブートストラップ(正帰還)を施し,C1に流れる電流を小さくする容量マルチプライヤ回路があります.図2(a)では,コンデンサの充電電圧を,ボルテージ・フォロワ回路で正帰還します.すると,R1とR2の両端の電圧は同じになり,R1>R2の関係にすれば,充電電流(i1)が小さくなり,見掛け上,コンデンサの容量が大きくなったように見えます.
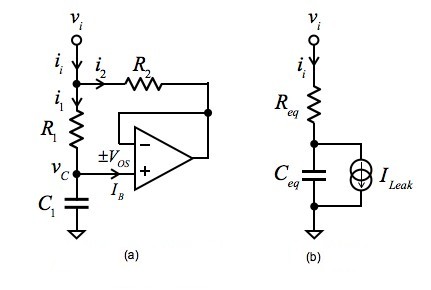
C1はCeqとなり大容量となる.ILeakを小さくするには,オフセット電圧が小さく,入力バイアス電流が少ないOPアンプを選ぶ.
図2(a)のブートストラップを使った容量マルチプライヤ回路を解析し,(b)の等価回路と比較してCeqとReqとの関係を調べます.図2(a)より,電圧(vi)を印加したときのi1は式4となります.
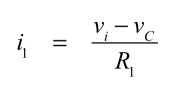 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
また,i2は式5となります.
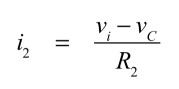 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
コンデンサの充電電圧は式6となります.
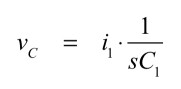 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
電圧(vi)を印加したときに流れる電流iiは,式4と式5を加算した電流なので,式7となります.
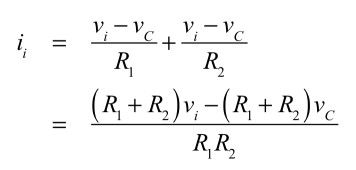 ・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・(7)
式4と式6を使うと,コンデンサの充電電圧は式8となります.
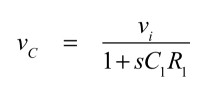 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式7と式8より,図1(a)のインピーダンスは式9となります.
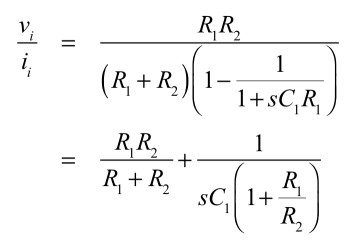 ・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・(9)
式9が,解答で示した式1の出所であり,ReqとCeqは解答の式3となります.
●直流誤差は回路で発生する漏れ電流
次に図2(a)のOPアンプに,入力オフセット電圧(±VOS)と入力バイアス電流(IB)があるときの直流誤差について解析します.この直流誤差は,回路で発生する漏れ電流で,印加する電圧(vi)に関係なく,図2(b)のILeakとなります.
入力オフセット電圧は,ボルテージ・フォロワ回路の出力オフセット電圧となり,式10に示すR2に流れる電流の誤差となります.
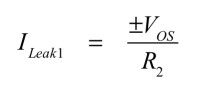 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
入力バイアス電流は,式11に示すR1側に流れる電流と,
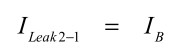 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
IBR1の電圧降下により,式12に示すR2側に流れる電流の誤差となります.
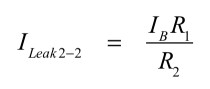 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
よって,式11と式12を加算した式13が入力バイアス電流による直流誤差となります.
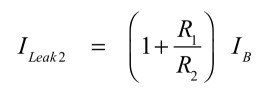 ・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・(13)
図2(b)の直流誤差(ILeak)は,式10の入力オフセット電圧に関係するものと,式13の入力バイアス電流に関係する誤差を加算したものなので,式14となります.
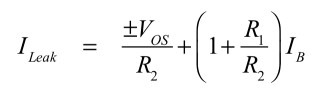 ・・・・・・・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・・・・・・・(14)
以上の解析より,直流誤差を小さくするには,使用するOPアンプの入力オフセット電圧と入力バイアス電流が小さいことが求められます.図1(a)では,入力バイアス電流が小さいJFET入力のOPアンプで,入力オフセット電圧が小さなものを選んでいます.
●長時定数回路のシミュレーション
図3(a)は,図2(a)の容量マルチプライヤ回路に,抵抗(R3)と,コンデンサ(C1)をリセットするスイッチ(S1)をつけた長時定数回路です.図3の回路定数と式3より,図3(b)の等価回路は,等価容量(Ceq)が10001μFの大きなコンデンサとなり,等価抵抗(Req)が99.99Ωとなります.リセット信号(Reset)により,スイッチがオープンになると充電を始め,長時定数が得られます.
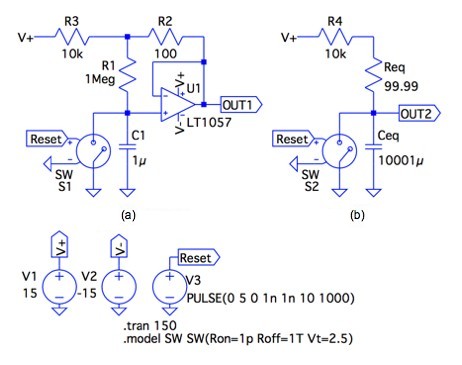
リセット信号によりスイッチがオープンとなり充電を始める.
図4は,図3のシミュレーション結果です.スイッチは10秒後にオープンとなり,長時定数回路へ充電を始めます.C1の電圧であるOUT1とOUT2は重なっており,式3の等価容量(Ceq)と等価抵抗(Req)の計算は正しいことが分かります.
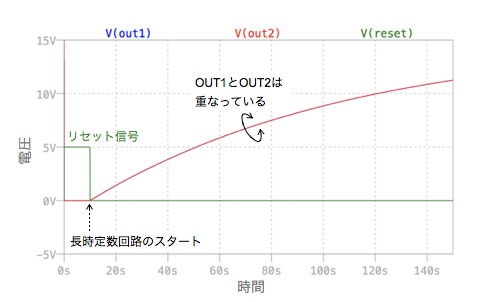
OUT1とOUT2は同じ長時定数となる.
●長時定数回路を応用したタイマー回路
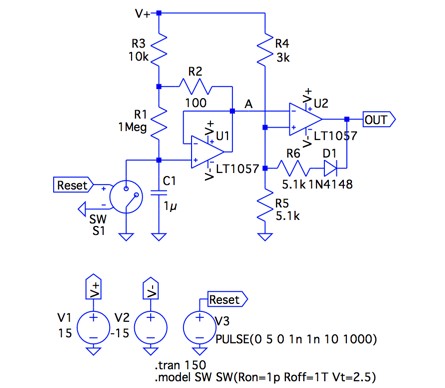
図5は,図3(a)の長時定数回路へ,OPアンプ(U2)と抵抗(R4,R5,R6)とダイオード(D1)を使ったヒステリシス・コンパレータを実装したタイマー回路です.ノードAはコンデンサの充電電圧と等しい電圧となり,その電圧がコンパレータの閾値より小さいと,出力は正側の最大出力電圧です.閾値を超えるとOPアンプの出力は負側の最大出力電圧となり,High/Lowの2値を出力します.
ヒステリシス・コンパレータの出力がHighからLowへ切り換わるときの閾値は,R4とR5の抵抗分圧で決まり,式15のようにC1充電カーブの63%になる値としました.こうすることで,Ceq(R3+Req)の積で決まる時間で,OUT端子のHigh/Lowが変わります.
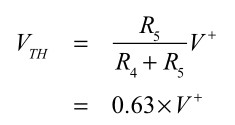 ・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
具体的な図3の時定数は式16であり,リセット信号から101秒後にOUT端子の電圧が変わるタイマー回路となります.
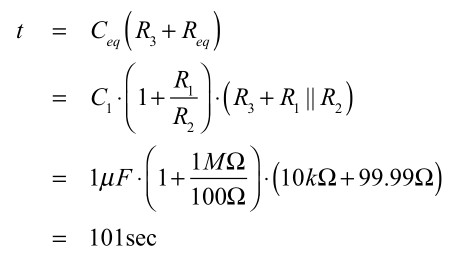 ・・・・・・・・・・・(16)
・・・・・・・・・・・(16)
長時定数回路出力電圧の63%でOUT端子は切り替わる.
図6は,図5のシミュレーション結果です.リセット信号は10秒後にスイッチをオープンにし,長時定数回路へ充電を始めます.OUT端子がHighからLowに切り替わる時間は100.4秒であり,式16の計算とほぼ合います.
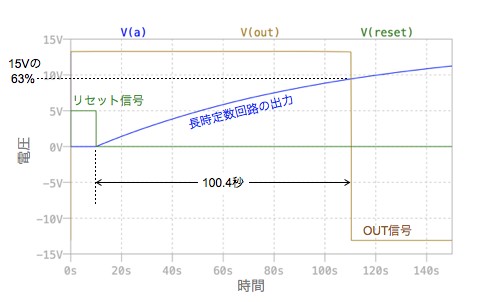
ブートストラップでC1が大容量になり,長時間のタイマー回路となる.
以上,ブートストラップを使った長時定数回路で,C1の容量を等価的に大きくみせることができ,その応用として長い時間のタイマー回路を作ることができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_025.zip
●データ・ファイル内容
Long_Time-Constant_circuit.asc:図3の回路
Timer.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










