容量を大きくみせるマルチプライヤ回路

図1(a)は,OPアンプ(U1)と抵抗(R1,R2)とコンデンサ(C1)を使い,C1の容量を大きくみせる容量マルチプライヤ回路です.図1(b)は,図1(a)の等価回路で,C2は,容量マルチプライヤ回路の等価容量と並列に接続したR3の抵抗で示しました.図1(a)の回路定数のとき,図1(b)の等価回路で表したC2とR3の値は,次の(a)~(d)のうちどれでしょうか.なお,OPアンプは理想とします.
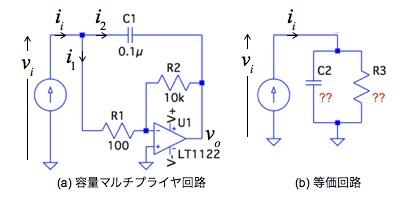
C2の容量とR3の抵抗の値はいくつか.
(b) C2= 10μF,R3=100Ω
(c) C2=10.1μF,R3=99Ω
(d) C2=10.1μF,R3=100Ω
図1(a)の電流源から右側をみたインピーダンスの式と,図1(b)のC2とR3を並列に接続したインピーダンスの式を比較することにより,求めることができます.
図1(a)の電流源より右側をみたインピーダンスを計算すると,図1(b)のC2は,C1を(1+R2/R1)で乗じた値となります.また,R3はR1と等しくなります.「R1=100Ω,R2=10kΩ」のとき,(1+R2/R1)=101なので,(d)の「C2=10.1μF,R3=100Ω」となります.
OPアンプを使った容量マルチプライヤ回路は,バイポーラトランジスタのベースとコレクタ間(MOSはゲートとドレイン間)にコンデンサを接続したミラー容量と同じで,回路のゲインで乗じた容量が得られます.OPアンプを使うと回路のゲインは抵抗比で得られるため,精度よく容量を大きくみせることができます.
●OPアンプを使った簡単な容量マルチプライヤ回路
図1(a)は,OPアンプを使った簡単な容量マルチプライヤ回路で「C1×回路のゲイン」が図1(b)のC2に相当するコンデンサとなります.図1(a)のR1は,OPアンプの反転端子(-端子)は,バーチャル・グラウンドなので,図1(b)のR3に等しくなります.ここでは,回路中の電流(ii,i1,i2)を使い,図1(a)容量マルチプライヤ回路の詳細な解析をおこない,図1(b)の等価回路と比較して,図1(a)と図1(b)の各定数の関係を導きます.図1(a)の電流源の両端の電圧をvi,OPアンプの出力をvoとすれば,反転アンプのゲインより,式1が成り立ちます.
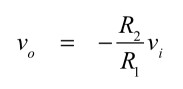 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
R1側に流れる電流(i1)は,式2となります.
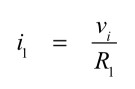 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
C1側に流れる電流(i2)は,式3となります.
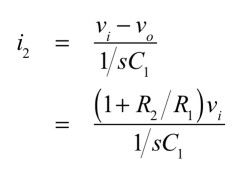 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
電流源から流れる電流(ii)は式4となります.
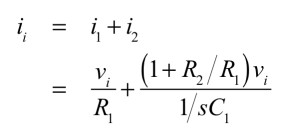 ・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・(4)
図1(a)のインピーダンス(vi/ii)は式5となり,C1を(1+R2/R1)のゲイン倍したコンデンサと,R1との並列接続であることが分かります.
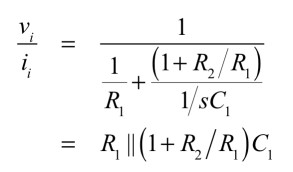 ・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・(5)
一方,図1(b)のインピーダンス(vi/ii)は式6となります.
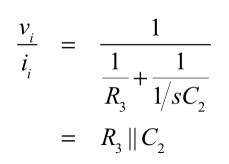 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
よって,式5と式6より,R1とR3,C1とC2の関係は,式7となります.
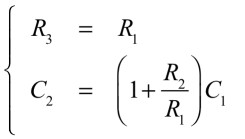 ・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7へ図1(a)の回路定数(R1=100Ω,R2=10kΩ)を代入すると,解答のC2=10.1μF,R3=100Ωとなります.
●マルチプライヤ回路をLTspiceで検証する
図2は,図1(a)と(b)をシミュレーションする回路です.図2(b)のC2,R3は解答で計算した値(C1=10.1μF,R3=100Ω)です.図2(a)(b)の入力は,小信号の交流電流源なので,Aノード,Bノードの電圧をプロットすると,インピーダンスの周波数特性となります.
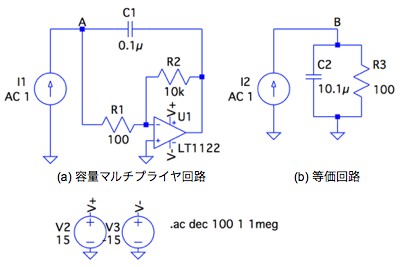
(b)のC2とR3は,計算で求めた等価容量と等価抵抗.
図3は,図2のシミュレーション結果です.1Hz~約10kHzまで2つのプロットは重なっており,この周波数領域では,図2(a)の容量マルチプライヤ回路は,図2(b)の等価回路で表せます.10kHz以上の周波数特性が合わないのは,OPアンプのオープン・ループ・ゲイン周波数特性の影響です.100Hz以下の低周波領域では,R3の抵抗値100Ωがみえてきます.この低周波領域では,コンデンサとして働きません.
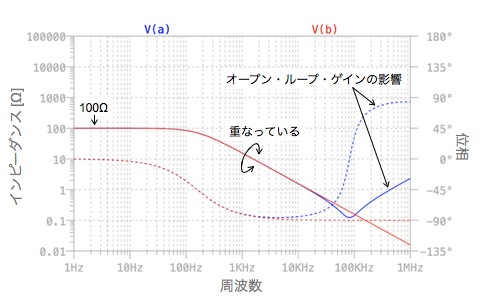
約10kHz以下では,AとBは重なっており,計算で求めた等価容量と等価抵抗であることが分かる.
●低周波領域まで使える容量マルチプライヤ回路
図4(a)は,図1の回路へボルテージ・ホロワ回路を実装し,R1に流れる電流はボルテージ・ホロワ回路から供給するようにした容量マルチプライヤ回路です.図4(b)は図4(a)の等価回路です.ボルテージ・ホロワ回路の同相入力インピーダンス(ZC),入力バイアス電流(IB)を加えました.ボルテージ・ホロワ回路の同相入力インピーダンス(ZC)は,非常に高く,また,OPアンプの入力バイアス電流(IB)は,JFET入力等のOPアンプを選べば無視できるほど小さいため,この2つは無視して回路解析をします.
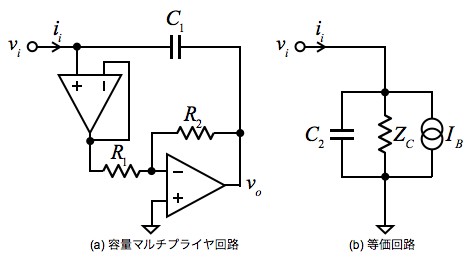
図4(a)の電流(ii)は式8となります.
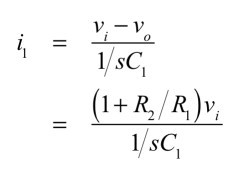 ・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
図4(a)の入力インピーダンスは,式8より式9となり
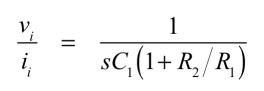 ・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・(9)
式9より,C1は,回路のゲイン(1+R2/R1)を乗じた容量となります.よって図4(b)等価回路のC2との関係は,式10となります.式9には式5の抵抗の項はありませんので,低周波でもコンデンサとして働きます.
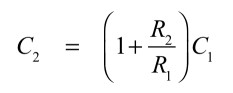 ・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
●容量マルチプライヤへボルテージ・ホロワを実装した回路をLTspiceで検証する
図5(a)は図4をシミュレーションする回路です.図5(b)はその等価回路です.図5(a)は可変容量とするため,R2を1kΩ,10kΩ,100kΩとなるように,反転アンプのゲイン(R2/R1)に相当する変数Gを「.stepコマンド」で変えています.図5(b)のコンデンサは,式10と変数Gにより,図5(a)の等価容量と同じとなるようにしました.
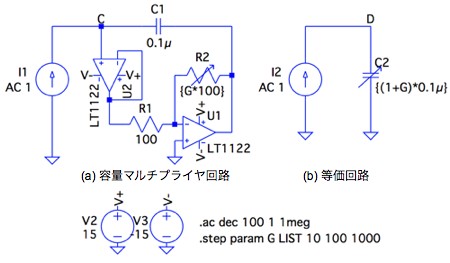
図6は,図5のシミュレーション結果です.CノードとDノードは重なっており,図5(a)の容量マルチプライヤ回路は,C1を(1+R2/R1)のゲインで乗じた容量となることが分かります.また,図3のシミュレーション結果と比べると,低周波側までコンデンサの周波数特性が得られます.注意点として,図5(a)の容量マルチプライヤ回路の等価容量は反転アンプのゲインに関係します.OPアンプは最大出力電圧以上の信号は扱えませんので,大きな等価容量を得るためにゲインを高くすると,OPアンプの最大出力電圧と反転アンプのゲインの関係から,小さな入力信号しか扱えません.
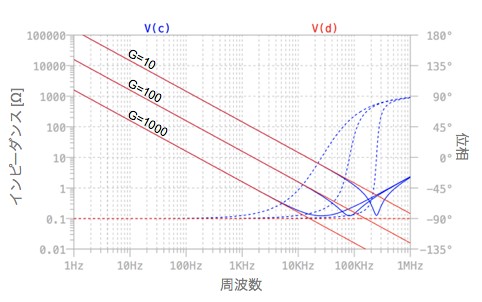
図3と比較すると,100Hz以下もコンデンサの周波数特性となる.
●ローパスフィルタへの応用
図7(a)は,容量マルチプライヤ回路を使ったローパス・フィルタ(LPF)です.図7(b)は,図7(a)の等価回路です.図5と同じように,可変容量とするため,R2を1kΩ,10kΩ,100kΩとなるように,反転アンプのゲイン(R2/R1)に相当する変数Gを「.stepコマンド」で変え,図7(b)のコンデンサは,式10と変数Gより与えます.この回路のコーナー周波数(fC)は,等価容量で変わります.通過域のゲインは,R3とRL1で決まりますので,ゲインを変えずにコーナー周波数(fC)を調整できます.
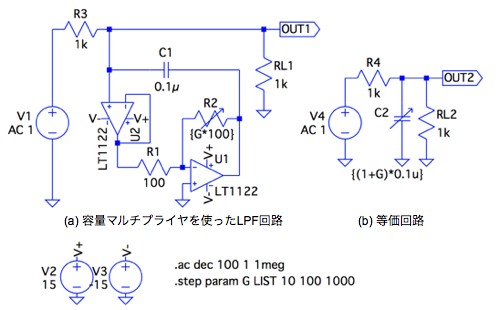
R2を変化させると可変容量となる.
図8は,図7のシミュレーション結果です.R2の調整により等価容量が変わり,通過域のゲインは一定(-6dB)で,コーナー周波数(fC)のみ変化しています.
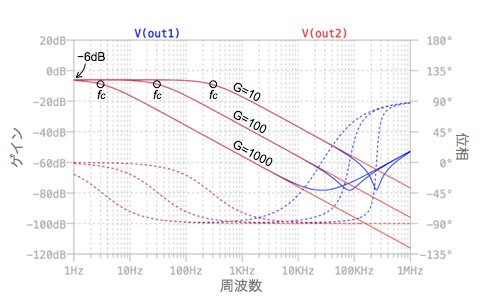
低周波のゲインはR3とRL1の抵抗比で決まり,-6dBとなる.
R2を変化させると等価容量が変わり,ゲインは一定のまま,LPFの周波数特性が変化する.
以上,解説したように,容量マルチプライヤ回路は,小さなコンデンサ(C1)に回路のゲイン(1+R2/R1)を乗じた大きな等価容量となります.ゲインを決める抵抗を可変抵抗にすれば可変容量となります.容量マルチプライヤ回路は,高いQが必要な共振回路等には不向きですが,フィルタ回路に応用できます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_023.zip
●データ・ファイル内容
Capacitance_Multiplier_1.asc:図2の回路
Capacitance_Multiplier_2.asc:図5の回路
LPF.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










