Y-Δ変換を使った積分回路
図1は，OPアンプ(U1)と抵抗(Ra，Rb，Rc，R1，R2，R3)とコンデンサ(C1)を用いた積分回路です．3つのY型に接続した抵抗(Ra，Rb，Rc)は，RaとRbが10kΩ，Rcが1kΩです．このY型の接続は，IN端子とOPアンプの反転端子間に，等価的な抵抗を作ります．図1の積分回路において，IN端子からOUT端子までのゲインが0dBとなる周波数は，次の(a)～(d)のどれでしょうか．なお，OPアンプは理想とします．
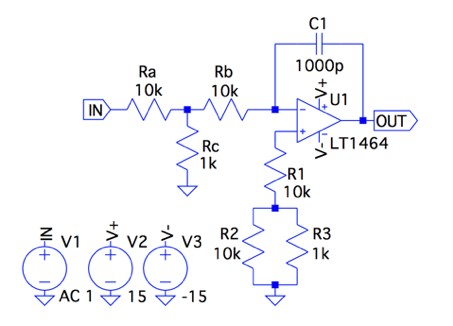
ゲインが0dBとなる周波数を求める.
Y型に接続した3つの抵抗(Ra，Rb，Rc)は，Y－Δ変換(スター・デルタ変換)を使い，IN端子とOPアンプの反転端子(－)間の等価的な抵抗へ置き換えることができます．ゲインが0dBとなる周波数は，Y－Δ変換後の抵抗ネットワークを図1へ適用し，入出力の伝達関数より求められます．Y－Δ変換は，3つの低い抵抗値で，等価的に高い抵抗を得ることができます.
図1のY型に接続したRa，Rb，Rcは，Y－Δ変換すると図2となり，Δ型に接続したRab，Rbc，Rcaで表すことができます．
ここで，Ra，Rb，Rcのアドミタンス(インピーダンスの逆数)は「Ya=1/Ra」，「Yb=1/Rb」，「Yc=1/Rc」となります．同じようにRab，Rbc，Rcaのアドミタンスは「Yab=1/Rab」，「Ybc=1/Rbc」，「Yca=1/Rca」となります．そこで，Rabは式1より120kΩとなります．
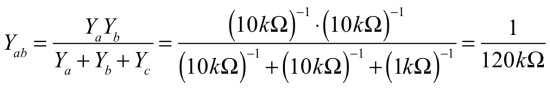・・・・・(1)
Rbcは，式2より12kΩとなり，
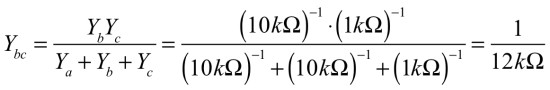・・・・・(2)
Rcaは，式3より12kΩとなります．
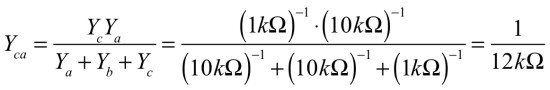・・・・・(3)
図1と図2を比べると，a点は入力端子(IN)，b点はOPアンプの反転端子(－)，c点はグラウンドです．また，図1の非反転端子(+)は，OPアンプを理想とすれば電流は流れませんのでグラウンドです．よってb点はバーチャル・グラウンドとなり，Rbcの両端の電圧は同じとなります．以上より，図1の伝達関数「vOUT(s)/vIN(s)」は式4となります．
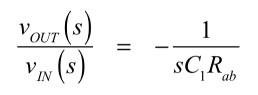・・・・・・・・・・・・・・・・・・・・・・・・・(4)
ゲインは式4の絶対値をとって式5となります．
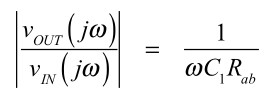・・・・・・・・・・・・・・・・・・・・・・・・(5)
式5が0dB(1倍)となる周波数は式6となります．そこで，解答は1.3kHzとなります.
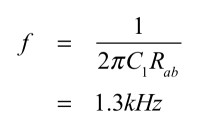・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
●Y－Δ変換について
Y－Δ変換は，低いインピーダンスを用い，等価的に高いインピーダンスを得るときに用いる手法です．図3は，Y－Δ変換を計算するための回路で(a)がY型の接続，(b)がΔ型の接続です．(a)と(b)の回路の3つの端子(a，b，c)からみたアドミタンスが同じ，すなわちVa，Vb，Vcを印加したとき，流れ込む3つの電流(Ia，Ib，Ic)が等しくなる関係を導くと，変換式が得られます.
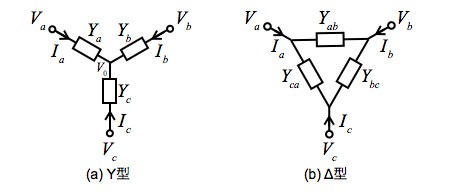
図3(a)の中心ノードのKCL(キルヒホッフの電流則)より，式7となります.
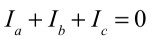・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
また，Va，Vb，Vc，V0の電圧を使い，3つの電流Ia，Ib，Icを求めると，式8となります.
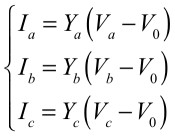・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式7と式8より，中心ノードの電圧V0は式9となります.
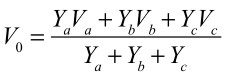・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
以上，図3(a)の3つの電流(Ia，Ib，Ic)は式10となります.
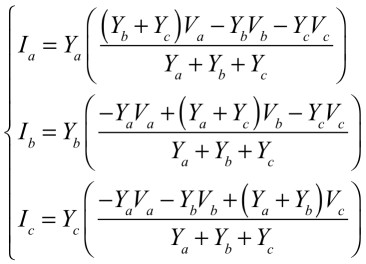・・・・・・・・・・・・・・・・・(10)
次に，図3(b)のΔ型の3つの電流(Ia，Ib，Ic)は式11となります.
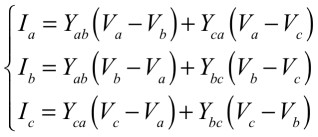・・・・・・・・・・・・・・・・・・・・(11)
式11を整理して式12とします.
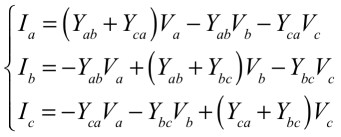・・・・・・・・・・・・・・・・・・・(12)
式10と式12の3つの電流(Ia，Ib，Ic)が各々等しいとして整理すると，解答の式1，式2，式3となります．このように，Y－Δ変換は3つの低い抵抗値(Ra，Rb，Rc)で，等価的にRabの高い抵抗値を得ることができます.
●基本的な積分回路の特性
まず始めに，図4(a)に示す抵抗(R1)とコンデンサ(C1)とOPアンプ(U1)で構成した，基本的な積分回路から解説します．図4(b)は，図1をY-Δ変換した積分回路で，図4(a)の基本的な積分回路との回路動作を比べるために用います．また，(b)の非反転端子(+)に接続した抵抗は，OPアンプの入力バイアス電流等の直流誤差を補償するための抵抗で，図4(a)の反転端子(－)からみた抵抗と同じになるようにしています.
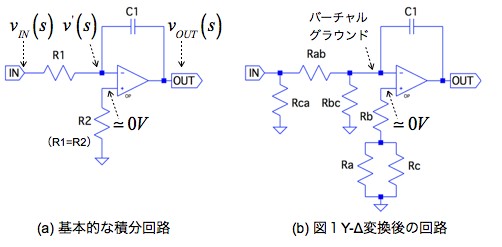
図4(a)の記号を用い，OPアンプのオープン・ループ・ゲインをA(s)として，積分回路の伝達関数を求めます．OPアンプの反転端子(－)の電圧をv’(s)とすれば，キルヒホッフの電流則(KCL)より，R1に流れる電流とC1に流れる電流は，式13の関係となります.
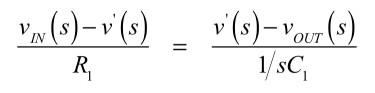・・・・・・・・・・・・・・・・(13)
OPアンプの非反転端子(+)は，電流が流れませんので0V(GND)となります．よって，両入力端子の電圧差はv’(s)となり，OUT端子の電圧(VOUT)は式14となります.
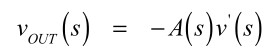・・・・・・・・・・・・・・・・・・・・・・・(14)
式13と式14より，基本的な積分回路の伝達関数は式15となります.
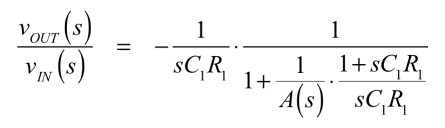・・・・・・・・・・・・(15)
ここで帰還率(β)は，式16となります．
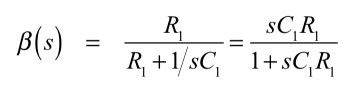・・・・・・・・・・・・・・・・・・(16)
なので，式15は式17で表せ，式17より，積分回路の伝達関数は，ループ・ゲインA(s)β(s)が誤差の要因となります．一般にOPアンプのオープン・ループ・ゲインA(s)は，非常に大きく，ループ・ゲインも1より十分大きいため，無視できます.
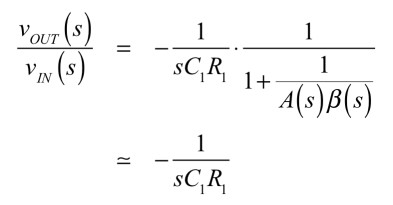・・・・・・・・・・・・・・・(17)
次に図4(a)の基本的な積分回路と，図4(b)のY-Δ変換した積分回路と比べます．図4(b)のRabは，図4(a)のR1に相当します．RcaはIN端子に接続する信号源の負荷となり，信号源が十分ドライブできる能力があれば，伝達関数に影響しません．Rbcは，バーチャル・グラウンドとなるOPアンプの反転端子(－)とGND間にあり，抵抗の両端の電圧差は，ほぼゼロと考えることができるため，こちらも無視できます．図4(a)と図4(b)は帰還率が異なりますが，OPアンプのオープン・ループ・ゲインA(s)が十分大きければ，ループ・ゲインも大きく，誤差は僅かとなります．よって，図4(b)のY-Δ変換した積分回路の伝達関数も「VOUT(s)/VIN(s)=－1/sC1Rab」で近似できます．
●積分回路の特性をシミュレーションで確認する
図5(a)は図1をシミュレーションする回路，図5(b)はY-Δ変換後の積分回路で，(a)との比較に用います．図5(b)のY-Δ変換した抵抗値(Rab，Rbc，Rca)は，解答の式1，式2，式3で求めた値です.
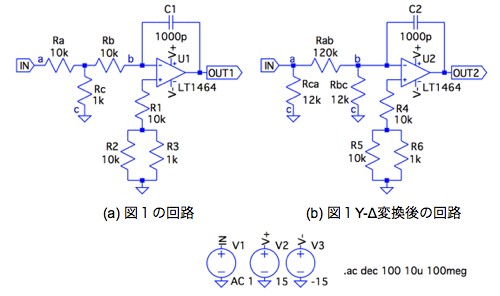
図6は，図5のAC解析の結果です．図5(a)の出力(OUT1)と図5(b)の出力(OUT2)の周波数特性は重なっており，(a)と(b)は同じ周波数特性であることが分かります．また，ゲインが0dBとなる周波数は，解答の1.3kHzであることも確認できます．積分回路として動作する周波数範囲は，入力に対し出力の位相が90度遅れるところです．図6の位相周波数特性より，おおよそ1Hz～10kHzの範囲となります．
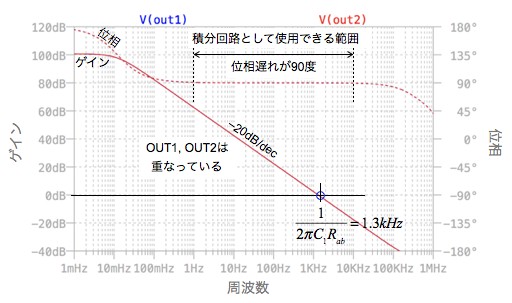
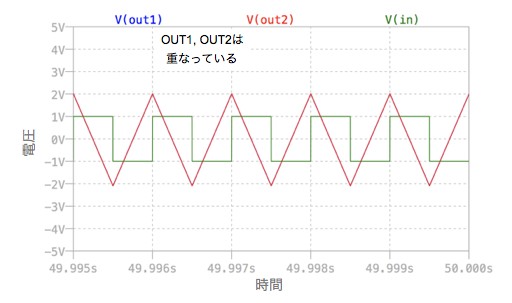
図7は，図5の回路を用い，振幅が±1V，立ち上がりと立ち下がり時間が1μs，周波数1kHzの矩形波「PULSE(-1 1 0 1u 1u 499u 1m)」を入力した解析結果です．回路が落ち着くまでの時間がかかるので，過渡解析の指定を「.tran 50 startup」と長くし，49.995秒～50秒までをプロットしました．矩形波を積分すると三角波になりますが，図7でも同様の波形が確認できます．
以上，解説したように，Y－Δ変換を用いることにより，等価的に高い抵抗値を得ることができます．またアプリケーション例として，スターデルタ変換を積分回路へ応用しました．ここでは詳細を示しませんでしたが，OPアンプを使った回路ですので，時間に対する出力電圧の最大変化は，OPアンプのスルーレートで制限されます．また負帰還安定性を評価するループ・ゲイン周波数特性の高周波側は，OPアンプの周波数特性となります．よって，積分回路が発振せずに安定に動作させるためには，OPアンプが十分に位相補償されていることが必要です.
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_017.zip
●データ・ファイル内容
Integrator_with_Star_Delta_Conv.asc：図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源＆アナログ回路入門・アーカイブs
