BPFの周波数特性からRLCの値を導く

■問題
アナログ回路の基礎 ― 初級

平賀　公久　Kimihisa Hiraga

　図1は，1μHのコイル(L)にコンデンサ(C)と抵抗(R)を直列に構成した，バンド・パス・フィルタ(BPF)です．このBPFの周波数特性を，中心周波数(f₀)が50MHz，帯域幅(BW)が2MHzにするには，CとRの値として正しい組み合わせは(a)～(d)のどれでしょうか．

図1　RLC直列回路を用いたバンド・パス・フィルタ
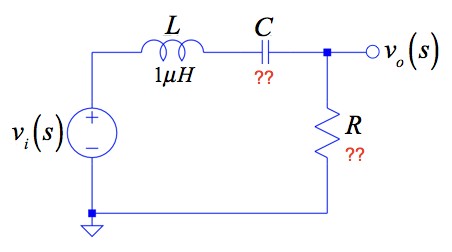
中心周波数50MHz，帯域幅2MHzになるCとRの値は？

(a)C：10pF，R：13Ω
(b)C：10pF，R：16Ω
(c)C：400pF，R：2Ω
(d)C：400pF，R：5Ω

■ヒント

　中心周波数(f₀)は，コイル(L)とコンデンサ(C)で決まり，中心周波数と帯域幅(BW)より，必要なQファクタ(Q)を計算し，抵抗(R)を求めます．帯域幅は中心周波数を境に低周波側と高周波側にあるカットオフ周波数の周波数差となります．

■解答

(a)C：10pF，R：13Ω

　RLC直列BPFの中心周波数は，式1に示すコイル(L)とコンデンサ(C)の共振周波数となります．そこで，式1を用い中心周波数(f₀)を50MHz，コイルを1μHとすれば，Cは10.1pFとなるので，小数点以下を四捨五入して10pFとします．　

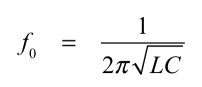・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　次に中心周波数付近の鋭さを示すQファクタは，中心周波数と帯域幅(BW)を用いると式2になります．式2を用いて，中心周波数が50MHz，帯域幅が2MHzより，Qファクタは25となります．

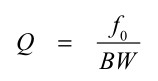・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　また，Qファクタは　抵抗，コイル，コンデンサを用いると式3の関係があります．式3を用い，Qファクタが25，コイルが1μH，コンデンサが10pFとして抵抗を求めると，Rは12.6Ωとなり，小数点以下を四捨五入して13Ωとなります．

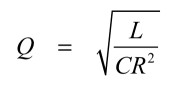・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　以上より，解答の(a)が導かれます．

■解説

　BPFの設計では，中心周波数や帯域幅，Qファクタを使って回路の特性を表します．今回は，受動素子のみで構成するRLC直列BPFの，中心周波数となる共振や中心周波数付近の周波数特性を示すQファクタ，帯域幅について詳しく解説します．

●RLC直列BPFの中心周波数は回路の共振周波数
　図1のRLC直列BPFの中心周波数は，その回路の共振周波数となります．図1の伝達関数は「s=jω」とすると式4となります．

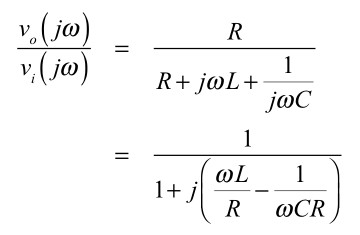・・・・・・・・・・・・・・・・・・(4)

　そのゲインを調べるため，絶対値をとると式5となります．

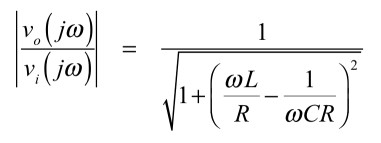・・・・・・・・・・・・・・・・・(5)

　共振時にコイルとコンデンサの組み合わせが短絡として作用し，入力(v_i)から見たRLC直列回路のインピーダンスは，抵抗(R)となります．よって，共振時に回路に流れる電流は同相となり，入力(v_i)と出力(v_o)の位相も同相となります．共振は式6の関係が成り立つときで「ω=ω₀=2πf₀」とすると，共振周波数は式1となり，式5のゲインは1倍となります．

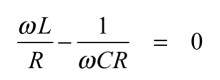・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

●Qファクタは最大エネルギーとエネルギー損失
　Qファクタは，蓄えられた最大のエネルギーと一周期あたりのエネルギー損失であり，式7となります．

・・・・・・・・・・・・・・・(7)

　図2のように，Qファクタの大小による周波数特性の違いをみると，Qファクタの値が大きければ大きいほど，BPFの周波数特性が鋭くなります．

図2　Qの大小による周波数特性の違い

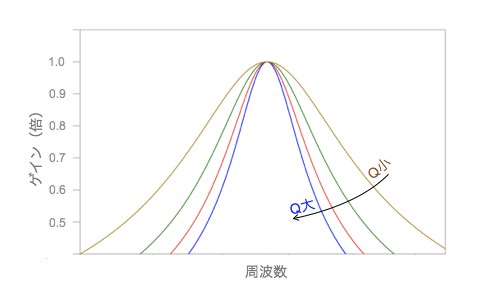
　ここで，RLC直列BPFのQファクタと，3つの部品であるコイル(L)，コンデンサ(C)，抵抗(R)との関係について，式7を用いて調べます．コイル(L)に蓄えられる最大のエネルギー(P_L)は，流れる電流のピーク値をI_pk，実効値をI_rmsとすれば「I_pk=√2*I_rms」ですので，式8となります．

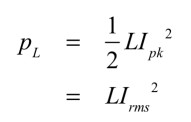・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

　また，一周期(T)の抵抗で消費されるエネルギーは式9となります．

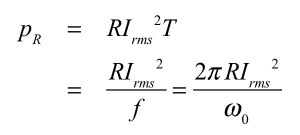・・・・・・・・・・・・・・・・・・・・・・(9)

　式8と式9を，Qファクタの定義式である式7へ代入すると，式10となり，コイルと抵抗によるQファクタが求まります．

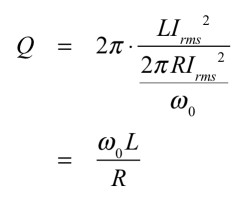・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　次にコンデンサによるQファクタを考えます．コンデンサに蓄えられるエネルギーは，電圧のピーク値をVpk，実効値をV_rmsとすれば式11となります．

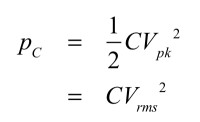・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)

　また，電圧の実効値と流れる電流には式12の関係があります

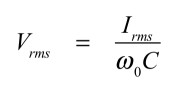・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)

　式12を式11へ代入した結果と，式9を用い，式7のQファクタを求めると式13となります．

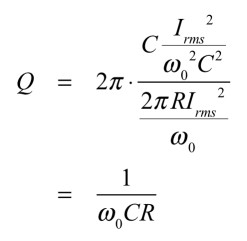・・・・・・・・・・・・・・・・・・・・・・・・・(13)

　コイルのQファクタを示す式10と，コンデンサのQファクタを示す式13を用いると，Qファクタとコイル，コンデンサ，抵抗の関係は，解答の式3となります．

●帯域幅は電力が半分になる周波数の差
　BPFの帯域幅(BW)は，電力が半分になる周波数の差です．これを電圧に直すと，図3に示す中心周波数(ω₀)のゲインから，1/√2倍(-3.01dB)となる2つのカットオフ周波数の差(ω₂-ω₁)となります．

図3　帯域幅(Band Width)の説明図
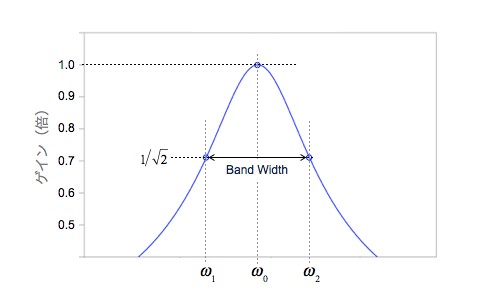
ω₂-ω₁が帯域幅となる．

　ここでは，BPFの中心周波数(ω₀)，帯域幅(BW)，Qファクタ(Q)の関係を導きます．はじめに式10より,「L/R=Q/ω₀」，式13より,「1/CR=Qω₀」を使い，式4を正規化して式14とします．

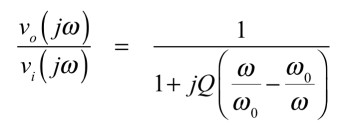・・・・・・・・・・・・・・・・・・(14)

　式14の絶対値は式15となり，その値が「1/√2」となる周波数ω₀がカットオフ周波数です．

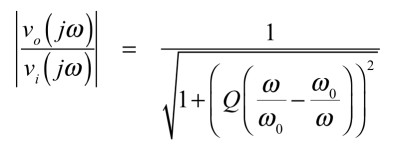・・・・・・・・・・・・・・・(15)

　式15を「1/√2」とするには，式14は式16となり，

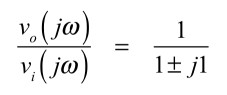・・・・・・・・・・・・・・・・・・・・・・・・・・(16)

　式14の複素数jにかかる項は式17となります．

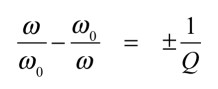・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)

　式17より，カットオフ周波数の低い方をω₁とすれば式18となり，

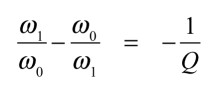・・・・・・・・・・・・・・・・・・・・・・・・・・・(18)

　高い方をω₂とすれば式19となります．

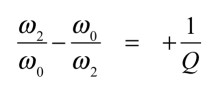・・・・・・・・・・・・・・・・・・・・・・・・・・・(19)

　式18と式19の2次方程式の正側の解は，式18が式20となり

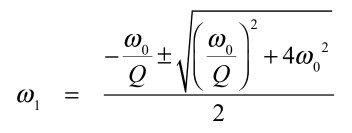・・・・・・・・・・・・・・・・・・(20)

　式19は式21となります．

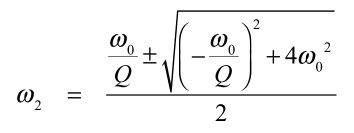・・・・・・・・・・・・・・・・・・(21)

　帯域幅は，式22となり，式22より，Qファクタは中心周波数を帯域幅で除算した値であり，解答の式2となります．

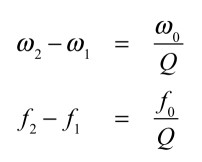・・・・・・・・・・・・・・・・・・・・・・・・・・・・(22)

●RLC直列BPFをLTspiceで確認する
　図4は図1のシミュレーション回路です．抵抗(R1)を「.stepコマンド」で13Ω，16Ω，21Ω，31Ωと変化させ，4つの抵抗値による周波数特性の変化を調べるようにしました．また「.measコマンド」で，中心周波数とそのときのゲイン，バンド幅を直読できるようにしました．

図4　図1をシミュレーションする回路
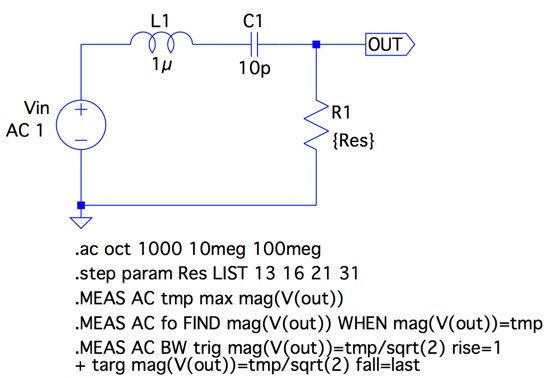
抵抗値を変えて，Qの変化を調べる．

　図5は，図4のシミュレーション結果です．図5より抵抗値が変化しても中心周波数が50.3MHz，ゲインが0dBで一定で，周波数特性の鋭さのみが変化することが分かります．

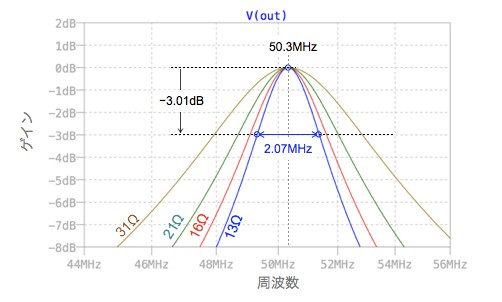
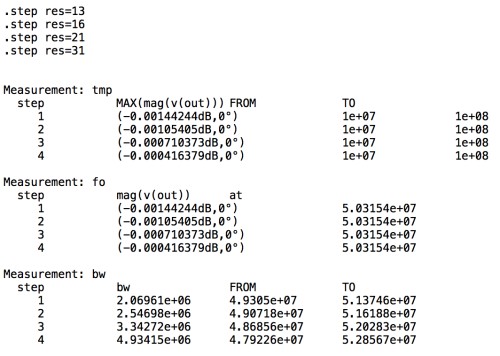
図5　図4のシミュレーション結果 R1=13Ωが解答のa)の回路定数．

　図6は「.measコマンド」で直読した結果のスナップショットです．図6より，解答と同じ抵抗(13Ω)のときのQファクタは，50.3MHz/2.07MHzより，Qファクタは24.3となります．これは，回路定数(L=1μH，C=10pF，R=13Ω)を用い，式3を使って求めたQファクタと同じになります．