ボード線図を用いたゲインと位相の解析

■問題
アナログ回路の基礎 ― 初級

平賀　公久　Kimihisa Hiraga

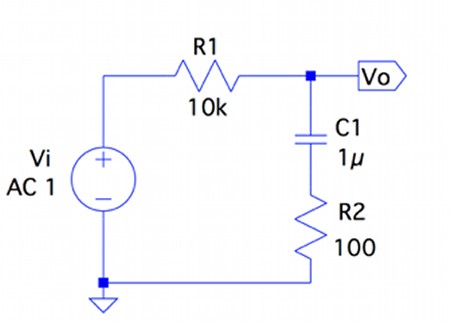
　図1は，抵抗(R₁，R₂)とコンデンサ(C₁)を使ったラグ・ネットワーク(Lag network)です．図1の伝達関数は式1となり，回路定数(R₁=10kΩ，R₂=100Ω，C₁=1μF)を用いるとポールの周波数(f_p)が「f_p=1/(2πC₁(R₁+R₂))=15.8Hz」，ゼロの周波数(f_z)が「f_z=1/2πC₁R₂=1.59kHz」となります．図1において，周波数が100kHzのときのゲインと位相が近いのは，次の(a)～(d)のどの組み合わせでしょうか．

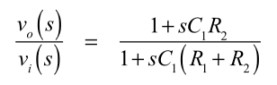図1　抵抗とコンデンサを使ったラグ・ネットワーク

・・・・・・・・・・・・・・・・・・・・・・・・(1)

(a)ゲイン：-40dB，位相：-45°
(b)ゲイン：-40dB，位相：0°
(c)ゲイン：-60dB，位相：-45°
(d)ゲイン：-60dB，位相：0°

■ヒント

　今回は，ボード線図を用いて，回路の周波数特性を求めます．式1から求まる一次進み要素と，一次遅れ要素より，ボード線図をプロットし，そのゲインと位相の周波数特性について調べると解答が分かります．図2は，ボード・プロット用の用紙です．LTspice4_011.zipをダウンロードしてご利用ください．

図2　ボード・プロット用の用紙

■解答

(b)ゲイン：-40dB，位相：0°

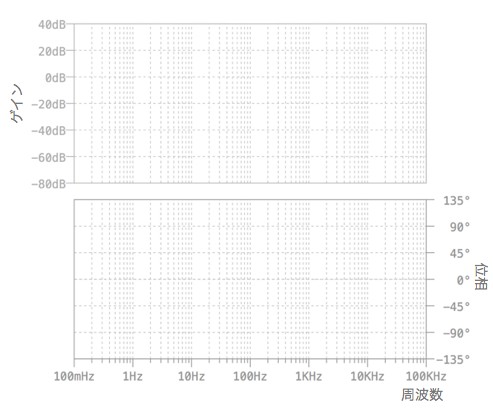
　式1の伝達関数の周波数特性は，一次進み要素と一次遅れ要素から成り，この2つの要素の和が，出力の周波数特性となります．ボード線図は，ゲインと位相それぞれの出力の周波数特性をプロットし，折れ線で近似します．
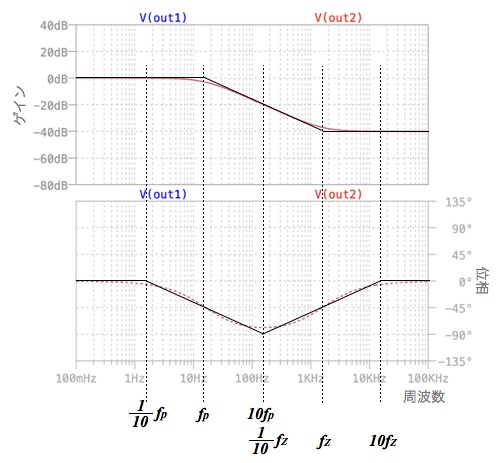
　図3が図1の出力の周波数特性を100mHz，ポールの周波数(1/10f_p，f_p，10f_p)，ゼロの周波数(1/10f_z，f_z，10f_z)，100kHzの計7箇所をプロットした出力のボード線図です．
　図3より，100kHzのゲインは-40dBで，位相は0°です．なので，答えは(b)となります．

図3　図1のボード線図

■解説

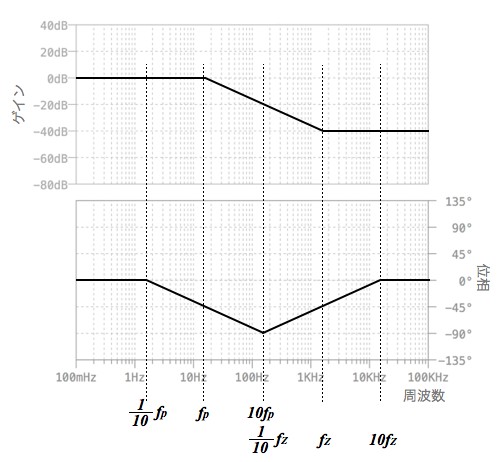
　ボード線図は，ゲインと位相の周波数特性のカーブを，直線を使った折れ線で近似したものです．ボード線図は，わずかな周波数の変化によるゲインと位相の変化を調べるのには適しません．しかし，広い周波数のゲインと位相の変化を迅速に調べることができます．解説では，図1の周波数特性が，一次進み要素と一次遅れ要素であることを調べ，それら二つの要素を使ったボード線図のプロット方法を解説します．

●周波数特性を調べる
　図1の周波数特性を計算して，伝達関数が，一次進み要素と一次遅れ要素の和であることを確かめます．図1の入力から出力までの伝達関数を求めると，式2となります．式2の中間の式は，式1となります．

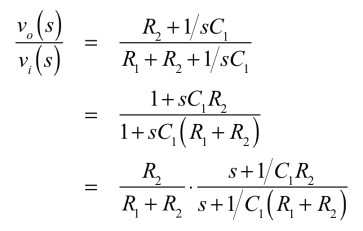・・・・・・・・・・・・・・・・・・(2)

　式3は，一次進み要素と一次遅れ要素を含んだ，双一次関数の一般式で，Kはゲインを表す定数，zはゼロに関する項，pはポールに関する項です．

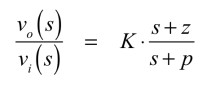・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　式2と式3を比較すると，zが式4

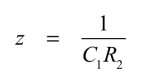・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

pが式5

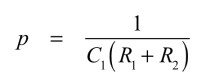・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

Kが式6となります．

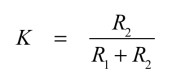・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　式3の双一次関数を「s=jω」とおくと式7となり，図4に示す3つのブロックが縦続接続した回路と同じになります．

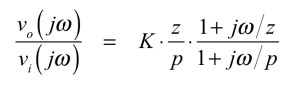・・・・・・・・・・・・・・・・・・・・・・(7)

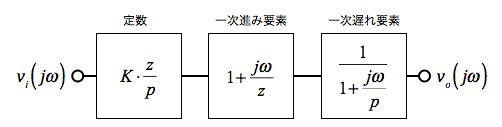
図4　式2の伝達関数を定数，一次進み要素，一次遅れ要素3つのブロックに分け縦続接続したブロック図

　ここで，定数のK*(z/p)は，式4，式5，式6を代入すると「K*(z/p)=1」となります．このように，図1の伝達関数は，一次進み要素と一次遅れ要素が合わさったものと考えることができます．
　式7より，デシベルで表したゲインは式8となります．

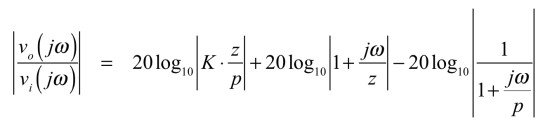・・・・・(8)

　また，位相は式9となります．

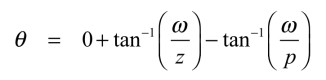・・・・・・・・・・・・・・・・・・・・(9)

　式8と式9よりゲインと位相は，定数，一次進み要素，一次遅れ要素の和となります．

●一次進み要素について
　次に，一次進み要素のゲインと位相を調べ，直線を使った折れ線で近似したボード線図は，どのようにプロットするかを解説します．式7の伝達関数の一次進み要素をT₂(jω)とすると，ゲインと位相は式10となります．

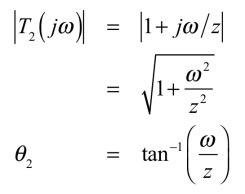・・・・・・・・・・・・・・・・・・・・・・・・・(10)

　式10を用いて，角周波数(ω)がゼロより十分低いとき(ω＜＜z)は，式11となります．

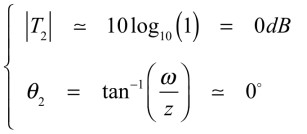・・・・・・・・・・・・・・・・・・・・・(11)

　角周波数(ω)が同じ値のとき(ω=z)は，式12となります．

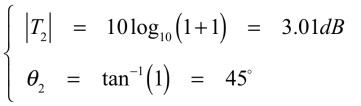・・・・・・・・・・・・・・・・・(12)

　角周波数(ω)が十分高いとき(ω＞＞z)は，式13となります．

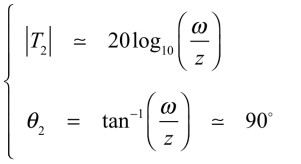・・・・・・・・・・・・・・・・・・・・・(13)

　図5は，一次進み要素のゲインと位相カーブ(赤色)を，直線を使った折れ線で近似したボード線図(黒色)で，f_zはゼロの周波数です．

図5　一次進み要素の周波数特性とそのボード線図

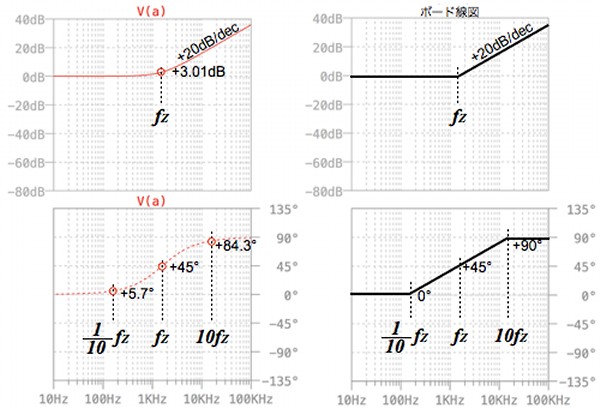
　ゲインは，式11の「ω＜＜z」の条件より，f_zより十分低い周波数のとき0dBで近似します．式12の「ω=z」では+3.01dBとなりますが，ボード線図では0dBとし，低周波からf_zまでは0dBの直線近似で表します．式13の「ω＞＞z」は，f_zより高い周波数領域で，+20dB/decの傾きでゲインが増加することを示しており，ボード線図では，f_zのゲインを始点に+20dB/decの直線近似で表します．これらを直線を使った折れ線で示したものがゲインのボード線図となります．
　次に位相は，式12の「ω=z」より，f_zのときは+45°です．f_zの1/10倍は+5.7°なので0°と近似します．10倍は+84.3°なので90°で近似します．式11の「ω＜＜z」の条件より，f_zより十分低い周波数は0°です．式13の「ω＞＞z」は，f_zより高い周波数では90°で近似します．これらを直線を使った折れ線で示したものが位相のボード線図となります．

●一次遅れ要素について
　式7の伝達関数の一次遅れ要素をT3(jω)とすると，ゲインと位相は式14となります．

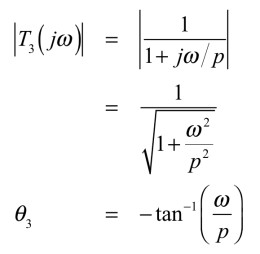・・・・・・・・・・・・・・・・・・・・・・・・(14)

　式14の角周波数(ω)が，ポールより，十分低いとき(ω＜＜p)，同じ値となるとき(ω=p)，十分高いとき(ω＞＞p)の3条件について，ゲインと位相を求めると，十分低いとき(ω＜＜p)が式15になります．

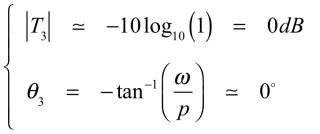・・・・・・・・・・・・・・・・・・・・(15)

　同じ値となるとき(ω=p)が式16になります．

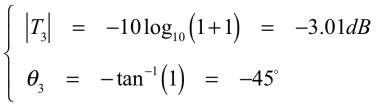・・・・・・・・・・・・・・・・(16)

　十分高いとき(ω＞＞p)が式17となります．

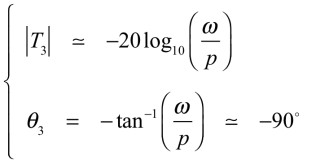・・・・・・・・・・・・・・・・・・・・(17)

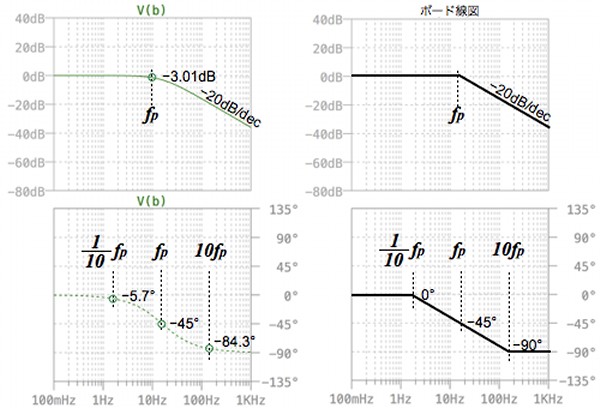
　図6は，一次遅れ要素のゲインと位相カーブ(緑色)を，ボード線図(黒色)で表した図です．f_pはポールの周波数です．一次遅れ要素のゲインと位相は，一次進み要素と同様な考えで，図6のように表せます．解答に示した図3のボード線図は，図5と図6のボード線図をグラフ上で和をとり，作成したもので，ゲインのボード線図が図3上，位相のボード線図が図3下となります．

図6　積分器の周波数特性とそのボード線図

●ボード線図とシミュレーションの比較
　図7は，図1をシミュレーションする回路で出力はOUT1です．また，図1は式7の一次進み要素と一次遅れ要素で成ることを確認するため，2つの要素の伝達関数を電圧制御電圧源へラプラス演算子を使った式で与え，同時にシミュレーションできるようにしました．具体的には，ゼロ(z)は「z=1/C₁R₂=10000(rad/s，ラジアン毎秒)」なので「1/z=100u」となり，LTspiceの電圧制御電圧源に，「Laplace=1+s*100u」を入れています．同様に，ポール(p)は「p=1/(C₁(R₁+R₂))=99(rad/s)」なので，「1/p=10.1m」として，Laplace=1/(1+s*10.1m)」としています．

図7　図1をシミュレーションする回路

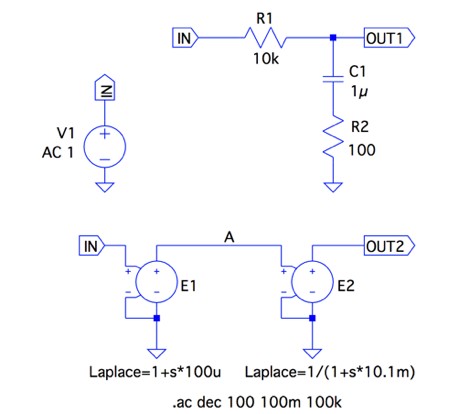
　図8が図7のシミュレーション結果です．図8より，OUT1とOUT2は重なっており，図1の伝達関数は，一次進み要素と一次遅れ要素が合わさったものだというのが分かります．また書き加えたボード線図(黒色)は，ゲインと位相の変化を，直線を使った折れ線で近似しており，広い周波数変化のゲインと位相の変化を調べることができます．