格子回路の角周波数とゲインの関係

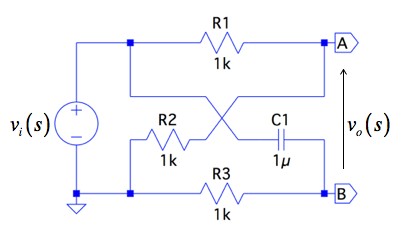
図1は,抵抗(R1,R2,R3)とコンデンサ(C1)を使った格子回路(Lattice network)です.この回路の入力(vi)から出力(vo)までの伝達関数を計算すると,ポールとゼロの角周波数は,ωCのとなり,R3とC1で決まります.ωCより十分低い角周波数をωL(ωC/100),また,十分高い角周波数をωH(ωC*100)とします.この場合,図1において,ωLとωHのときの,ゲイン[vo(s)/vi(s)]が正しい組み合わせは(a)~(d)のどれでしょうか.ここで,sはラプラス演算子(s=jω)です.
(b)ωL:1倍,ωH:1/2倍
(c)ωL:1/2倍,ωH:1倍
(d)ωL:1/2倍,ωH:1/2倍
図1の格子回路は,ブリッジ回路へ変形すると分かりやすくなります.変形したブリッジ回路で,入力からA点とB点の電圧を求め「vo(s)=vA(s)-vB(s)」より,周波数の変化に対するゲインの変化を計算すると求められます.
図1の格子回路は,APF(All Pass Filter),または,位相器と呼ばれ,周波数の変化に対し,ゲインは1/2倍(-6.02dB)で一定となり,位相だけが変化する回路です.図1の伝達関数[vo(s)/vi(s)]より「s=jω」として,ゲインと求めると式1となります.式1の右辺にある複素関数の「1-jω/ωC」と「1+jω/ωC」は,絶対値が同じです.よって,ゲインは周波数に関係なく1/2倍(-6.02dB)であり,解答の(d)となります.なお,位相については,後述の解説で計算し要点を示します.
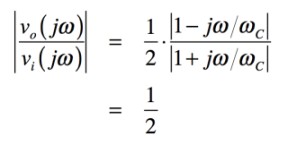 ・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・(1)
●ポールとゼロについて
回路の周波数応答を表すとき,入力から出力への伝達関数を用います.ここでは,伝達関数中にあるポールとゼロについて,図2を用いて解説します.
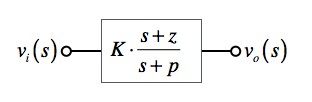
sはラプラス演算子,Kは回路のゲイン,zはゼロに関係する項,pはポールに関係する項を表す.
図2は,式2に示す伝達関数を持った回路をブロック図で示しました.式2は,1次LPF(Low Pass Filter)や1次HPF(High Pass Filter),また,今回のAPF(All Pass Fileter)などの伝達関数の一般式で,双一次関数と呼びます.
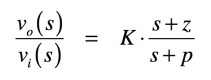 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式2中のsがラプラス演算子,Kがゲイン,zがゼロに関係する項,pがポールに関係する項を表しています.また,ゼロは零点,ポールは極とも呼びます.ゼロは,式2のゲインがゼロ,すなわち「vo(s)/vi(s)=0」となるsの値であり-zとなります.また,ポールはゲインが無限大「vo(s)/vi(s)=∞」となるsの値で-pとなります.ゼロやポールは,回路の周波数特性を検討するときに使います.
●伝達関数の振幅と位相
フィルタの特性や,アンプの周波数特性等では,振幅の周波数特性や位相の周波数特性が重要です.これらは伝達関数から計算ができ,ここでは式2を例に解説します.式2の双一次関数を「s=jω」とおくと式3となります.
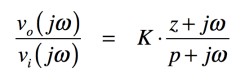 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
振幅は,式3の複素関数の絶対値をとって式4です.
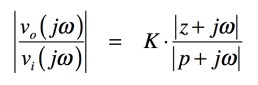 ・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・(4)
また,位相は式5となり,θが正なら位相進み,負ならば位相遅れとなります.ここでKの位相が正なら同相なので0°,負ならば位相が反転した逆相なので180°です.
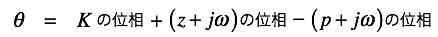 ・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・(5)
式5において,Kが正ならば,複素関数の実部と虚部より,位相は式6となります.
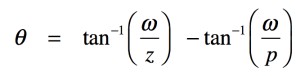 ・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・(6)
●伝達関数を求め振幅と位相の周波数特性を調べる
図1の格子回路は,ブリッジ回路へ変形でき,それを図3へ示します.図3を用いたほうが直感的に分かりやすいと思います.
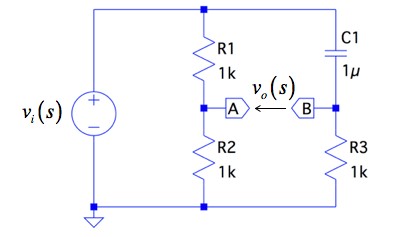
図3のA点の電圧は,抵抗R1とR2の分圧回路であり,ここでは「R1=R2」ですので式7となります.
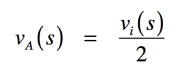 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
B点の電圧は,C1とR3のインピーダンスの分圧回路ですので,式8となります.
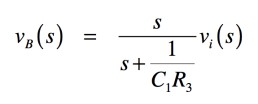 ・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・(8)
出力電圧vo(s)は,A点の電圧からB点の電圧を減算したものなので,式9となります.
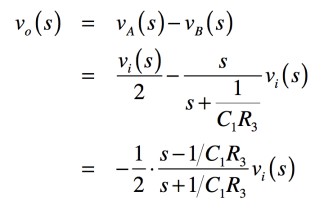 ・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・(9)
式9のラプラス演算子を「s=jω」,「ωC=1/C1R3」とおくと,図1の伝達関数は式10となります.
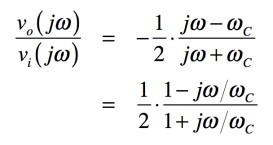 ・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・(10)
式10より,図3の振幅は,複素関数の絶対値をとって解答の式1となり,ゲインは周波数に関係なく1/2倍(-6.02dB)となります.次に位相は,式10へ式6の関係を用いると式11となります.
 ・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・(11)
ここでωCは「2πfC=1/C1R3」であり「R3=1kΩ」,「C1=1μF」を用いると「fC=159Hz」です.また,「ωL=2πfL=ωC/100」より「fL=1.59Hz」,同様に「ωH=2πfH =ωC*100」より「fH=15.9kHz」です.この3つの周波数における位相を周波数の低い順(fL,fC,fH)で調べると,fLは式12になります.
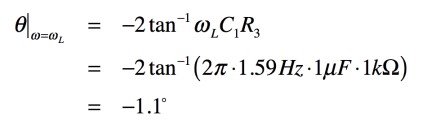 ・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・(12)
fCは式13になります.
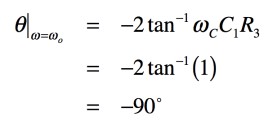 ・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・(13)
fHは式14となり,周波数の変化で,位相が変わることが分かります.位相は負であり,図1の回路は位相が遅れます.
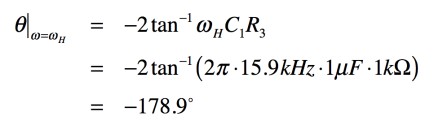 ・・・・・・・・・・・・(14)
・・・・・・・・・・・・(14)
●振幅と位相の変化をLTspiceで確かめる
図4は,図1をシミュレーションする回路です.出力電圧は,A点とB点の差をプロットして,そのゲインと位相を調べます.
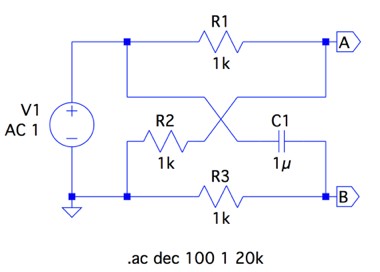
図5は,シミュレーション結果です.ゲインは,1/2倍(-6.02dB)で一定であることが分かります.また,位相は周波数によって変化し,式12,式13,式14で調べた値と一致しています.このように,図1の回路は周波数が変化してもゲインは一定であり,位相だけが変わるAPF(位相器)の特性であることが分かります.
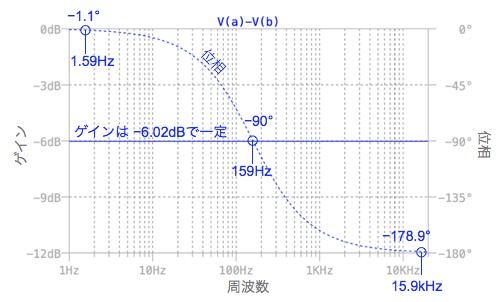
ゲインは,-6.02dBで一定.位相は周波数により変化している.
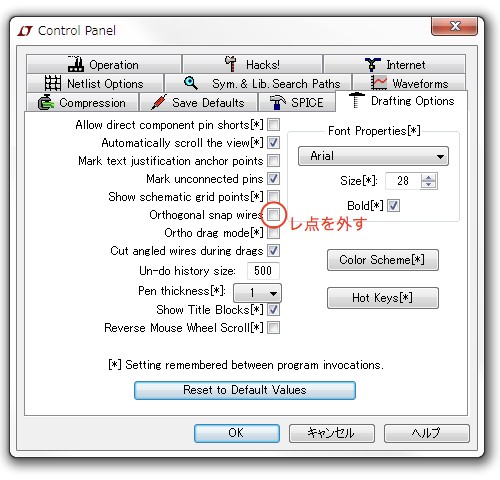
最後に,回路を対象にみせるため,図1の回路のように斜め配線を使うときがあります.LTspiceでは,図6に示すコントロール・パネルで「Orthogonal snap wires」のレ点を外すことで,斜め配線が可能となります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_009.zip
●データ・ファイル内容
APF.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










