一次遅れ回路のゲインと位相

■問題
アナログ回路の基礎 ― 初級

平賀　公久　Kimihisa Hiraga

　図1は，抵抗(R₁)とコンデンサ(C₁)を使った一次遅れ回路に負荷抵抗(R_L)がついた回路です．回路定数は，抵抗R₁とR_Lが1kΩで，コンデンサ(C₁)が1μFとします．図1の回路において，入力v_i(s)から出力v_o(s)までの伝達特性で，1Hzのゲインと位相が-45°遅れになる周波数の値として正しい組み合わせは(a)～(d)のどれでしょうか.

図1　R₁とC₁の一次遅れ回路に負荷抵抗R_Lがついた回路

(a)ゲイン：0dB，周波数：159Hz
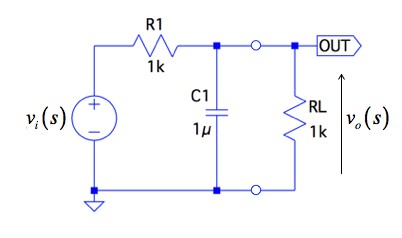
(b)ゲイン：0dB，周波数：318Hz
(c)ゲイン：-6dB，周波数：159Hz
(d)ゲイン：-6dB，周波数：318Hz

■ヒント

　R₁とC₁の一次遅れ回路へ負荷抵抗(R_L)を接続すると，出力のゲインと位相は，負荷抵抗の影響を受けて，R₁とC₁で決まるゲインと位相から変化します．回路の伝達関数v_o(s)/v_i(s)を求め，その絶対値であるゲインと，位相の関係を計算すると求められます．
　ゲインと位相を図式で表すのは，ベクトル軌跡とボード線図があります．ここでは，前者のベクトル軌跡を用いて解説します．ベクトル軌跡は，角周波数(ω)を0～∞までスイープしたときのベクトル先端の軌跡をプロットしたものです．調べたい角周波数(ω)を入れることにより，回路のゲインと位相が分かります.

■解答

(d)ゲイン：-6dB，周波数：318Hz

　図1の伝達関数v_o(s)/v_i(s)を求めるとき「R₁=R_L=R」としました．伝達関数v_o(s)/v_i(s)で「s=jω」とし，その絶対値をとると式1となります．1Hzのゲインは，0.5倍なので，デシベルで表すと小数点以下を切り捨てると-6dBとなります．

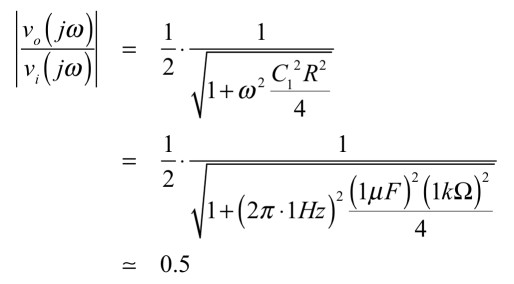・・・・・・・・(1)

　また，位相が-45°となるのは，式2で「ω=2/C₁R」のときですのでC₁が1μF，Rが1kΩなので「f=2/2πC₁R=318Hz」となります.

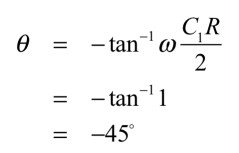・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

■解説

●基本的な一次遅れ回路について
　図2は，抵抗(R₁)とコンデンサ(C₁)で構成した基本的な一次遅れ回路です．ここでは，図2をベクトル軌跡を用いて，周波数の変化に対するゲインと位相を解説します．図2の一次遅れ回路は，ロー・パス・フィルタとしてよく用いられる回路です．また，ベクトル軌跡は，角周波数(ω)の変化に対し，ゲインと位相の変化を図式で表現するものです．

図2　R₁とC₁の基本的な一次遅れ回路

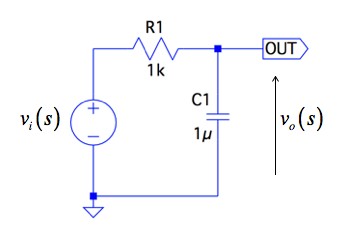
　まず，出力のゲインと位相を調べるため，図2の伝達関数v_o(s)/v_i(s)を求めると「s=jω」と置換して式3となります．

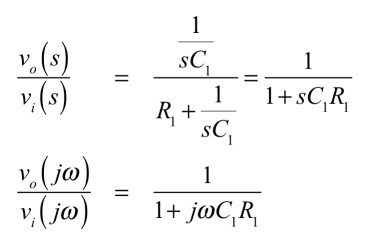・・・・・・・・・・・・・・・・・(3)

　ベクトル軌跡は，X軸を実軸，Y軸を虚軸とした複素平面で表し，角周波数(ω)が0～∞へ変化したときの，ベクトルの先端をプロットしたものです．このベクトルの長さがゲインであり，実軸との角度が，入力から出力への位相差となります．
　ベクトル軌跡を描くため，式3を式4のように変形し，角周波数(ω)が0～∞へ変化させます．このときのベクトル軌跡が図3となります．図2の基本的な一次遅れ回路は，実軸が0.5，虚軸が0を中心とした半円となります．

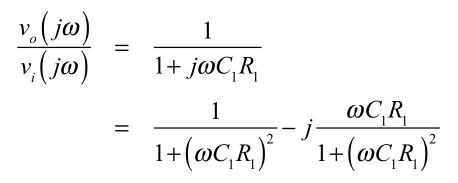・・・・・・・・・・・(4)

図3　　v_o(jω)/v_i(jω)=1/jωC₁R₁のベクトル軌跡

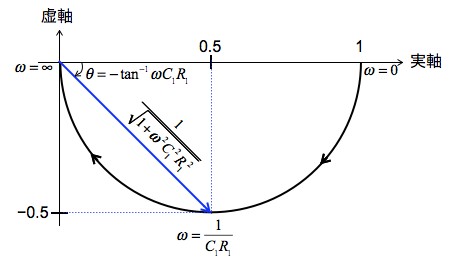
　式4より，ゲインは，複素関数の絶対値であり，1Hzの周波数では，式5のようにゲインが約1倍(0dB)となります．

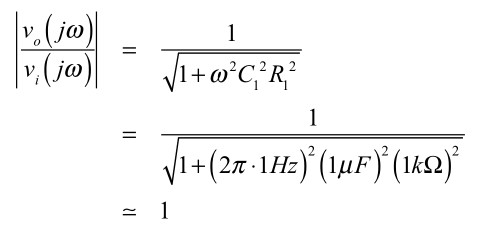・・・・・・・・・・(5)

　また，位相は実軸からの角度なので，式6のように，-45°になるのは「ω=1/C₁R₁」であり，周波数fに直すと「f=1/2πC₁R₁=159Hz」となります．

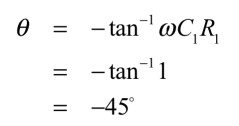・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　図3の青色で示したベクトルは「ω=1/C₁R₁」の場合です．底辺が青色のベクトルとした三角形とすれば，0.5の等しい辺を持った二等辺三角形です．その底角は45°であることが分かります．また，「ω=1/C₁R₁」のときのゲインは，青色の底辺の長さなので，0.5*√2倍，すなわち1/√2倍(-3.01dB)になります．

●一次遅れ回路のゲインと位相を伝達関数で確認する
　図1についても，C₁とR_Lの合成インピーダンスとR₁の分圧回路より伝達関数を求め，角周波数(ω)が0～∞へ変化したときのゲインと位相の変化を調べます．C₁とR_Lの合成インピーダンスは式7となります．

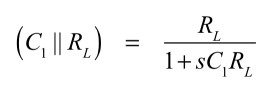・・・・・・・・・・・・・・・・・・・・・・・・(7)

　式7を使い，入力から出力への伝達関数v_o(s)/v_i(s)を求めると式8となります.

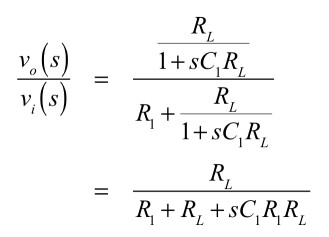・・・・・・・・・・・・・・・・・・・・(8)

　ここで，図1は，R₁とR_Lの抵抗値が等しいため「R₁=R_L=R」として「s=jω」と置換して，式9となります．

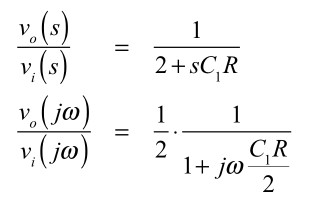・・・・・・・・・・・・・・・・・・・・・(9)

　式9と，前述のR_Lが無いときの式3を比べると，図1の直流に近い低周波のゲインは，式3より1/2倍(-6.02dB)となり，また，位相が-45°になる周波数は，2倍の318Hzとなります．なお，式9の複素関数の絶対値とその位相を計算したものが，解答の式1と式2となります.

●一次遅れ回路のゲインと位相をLTspiceで確認する
　図4は，図1と図2のゲインと位相をAC解析でシミュレーションする回路です．

図4　図1と図2をシミュレーションする回路

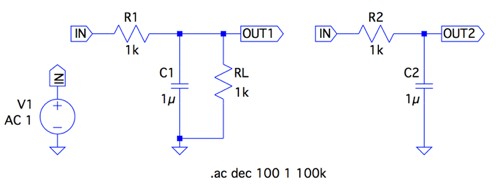
　図5がそのシミュレーション結果のプロットです．

図5　図3のシミュレーション結果

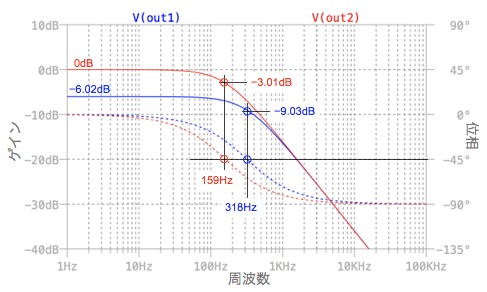
　図1の出力に相当するOUT1を調べると，1Hzのゲインが-6dBで，位相が-45°になる周波数は318Hzで，解答と同じであることが分かります．図2の出力であるOUT2と比べると，負荷抵抗(R_L=1kΩ)により，ゲインと位相が影響を受け，低周波(ここでは1Hz)のゲインが0dBから-6.02dB(1/2倍)へ低くなります．位相が-45°になる周波数は，159Hzから318Hz(2倍)へ高くなって，式9と式3を比較した結果と一致しています．
　また，負荷抵抗を接続したとき，図3の基本的な一次遅れ回路のゲインと位相を保つには，基本的な一次遅れ回路と負荷抵抗(R_L)の間に，ゲインが1で，入力インピーダンスが1kΩより十分高いバッファ回路が必要となります.

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice4_007.zip

●データ・ファイル内容
LPF.asc：図4の回路