重ね合わせの理で抵抗値を求める

図1は,NPNトランジスタ(Q1)のエミッタとGND間に抵抗(RE)を入れたエミッタ・ホロワ回路です.NPNトランジスタ(Q1)のベースには,直流のバイアス電圧(VBE)700mVとVSの小信号の交流電圧源を印加します.図1において,ベース端子から右側をみた低周波の入力インピーダンス(Zin)が1MΩ以上になるのは,抵抗(RE)の値が(a)~(d)のときでしょうか.ここで,REの値を(a)~(d)に変えたときのコレクタ電流(IC)とベース電流(IB)は,図1の中に記載しました.また,トランジスタ(Q1)のアーリー電圧(VA)は100Vで,熱電圧(VT)は26mVとします.
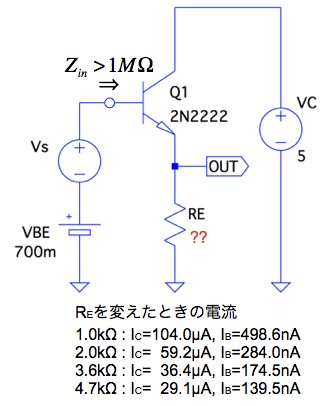
ベース端子から右側をみた低周波の入力インピーダンスが1MΩ以上となるREの値は?
今回は,重ね合わせの理の解説をエミッタ・ホロワ回路の入力インピーダンスを求めることで解説します.NPNトランジスタ(Q1)をπ型等価回路へ置き換え,ベース端子の小信号電圧(vb)と小信号のベース電流(ib)より,オームの法則を使って「Zin=vb/ib」を計算することで求められます.
図1のNPNトランジスタ(Q1)のベースから右側をみた入力インピーダンスは式1となります.
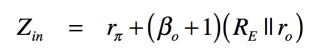 ・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・(1)
ここで,バイポーラ・トンランジスタの入力抵抗は「rπ=βo/gm」,電流増幅率は「βo=IC/IB」,トランスコンダクタンスは「gm=IC/VT」,出力抵抗は「ro=VA/IC」で求めます.
図1に記載した,コレクタ電流(IC)とベース電流(IB)を使い,式1の各項を計算して入力抵抗を求めると,表1となります.これより,図1の入力インピーダンス(Zin)が1MΩ以上となるのは,(d)の4.7kΩとなります.
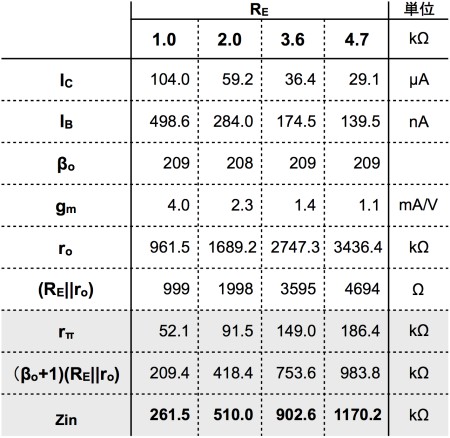
(d)の4.7kΩのとき,入力インピーダンス(Zin)は1MΩ以上となる.
●重ね合わせの理とは
キルヒホッフの法則を「IoT時代のLTspiceアナログ回路入門 001 ―― キルヒホッフ法則で抵抗値を求める」で解説しましたが,その他の回路計算手法として,重ね合わせの理を使うと便利なときもあります.重ね合わせの理は,複数個ある電圧源,電流源を1つ残して各々回路解析し,その結果を重ねる(解を加え合わせる)ことにより回路解析できます.回路の電圧源や電流源を1つ残すときは,他の電圧源をショート,他の電流源をオープンにして計算します.
●重ね合わせの理を使い入力インピーダンスを求める
図1のエミッタ・ホロワ回路をバイポーラトランジスタのπ型等価回路を使って表したのが図2(a),2つある電流源のうち1つを残し,重ね合わせるのが図2(b),(c)です.この例で,電圧源はありませんので,片方の電流源を残すときには,残りの電流源はオープンとしています.図2(a)の入力インピーダンス「Zin=vb/ib」を求めたいので,図2(b),(c)をvb1,vb2とし,「vb=vb1+vb2」と解を加えます.
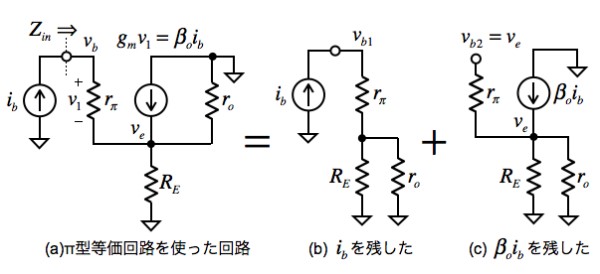
まず,図2(b)のvb1は,rπと(RE||ro)の直列回路にibが流れることにより発生する電圧ですから,オームの法則より式2となります.
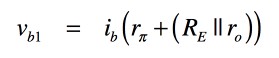 ・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・(2)
同様に,図2(c)のvb2は式3となります.
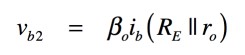 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
図2(a)のvbは,重ね合わせの理より「vb=vb1+vb2」ですので,式4となります.
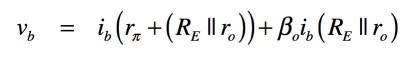 ・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・(4)
式4より,入力インピーダンス「Zin=vb/ib」は式5となり,解答の式1となります.
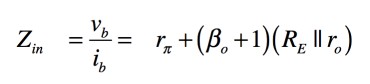 ・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・(5)
このように,他の電圧源や電流源を回路から削除して計算ができるため,図2の例では,多くの計算をしないでvb1,vb2の計算ができ,それを重ね合わせることにより回路の解析が楽になることがあります.
●キルヒホッフの法則を使い入力インピーダンスを求める
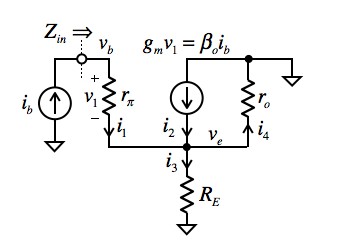
比較のため,図1をキルヒホッフの法則を使って計算し,式5と同じになるか確かめます.図3はπ型等価回路を使ったエミッタ・ホロワ回路の等価回路です.キルヒホッフの電流則(KCL)より,エミッタのノードに流れ込む電流の総和はゼロですので,式6となります.
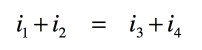 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
各々の電流を,図3の記号を使うと式7となります.
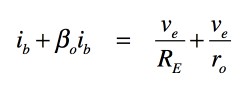 ・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・(7)
次にキルヒホッフの電圧則(KVL)より「ib→ベース→エミッタ→RE→GND」の閉路よりベースの電圧vbは,式8となります.
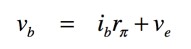 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式7をveで整理すると式9となります.
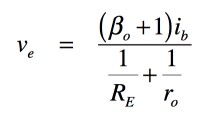 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
式9のveを式8へ代入し,入力インピーダンスの「Zin=vb/ib」へ変形すると,式10となります.
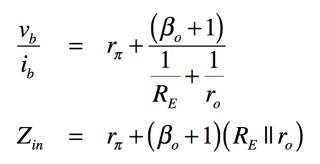 ・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・(10)
式5と式10は同じです.キルヒホッフの法則を使う方が,重ね合わせの理より,計算量が少し増えます.この例だと,重ね合わせの理のほうが,回路解析の計算は便利といえます.
●LTspiceを使いREを変化させたときの入力インピーダンスを確認する
図4は,図1の入力インピーダンスをシミュレーションする回路です.NPNトランジスタのベース電圧は700mVで固定します.REを変化させたときのコレクタ電流(IC)とベース電流(IB)は,図1に記載したとおりです.この回路で,VSは小信号の信号源であり,AC解析を用いて,低周波での入力インピーダンスをシミュレーションします.入力インピーダンスは,NPNトランジスタのベース電圧(vb)とベースに流れ込む電流(ib)を使い計算します.
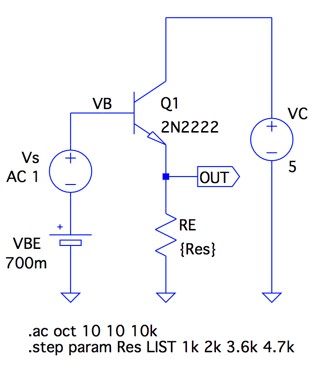
REは「.stepコマンド」で変化させた.
図5がシミュレーション結果です.グラフには100Hzの入力インピーダンスを記入しました.このように,表1で計算した入力インピーダンスとほぼ同じ結果であることが確認できました.
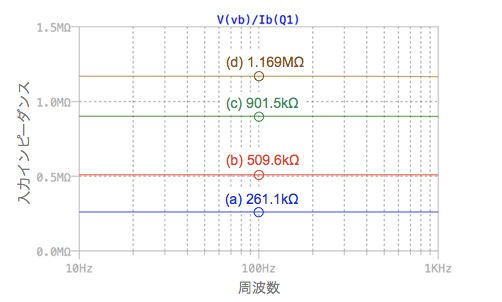
表1の重ね合わせの理を使った計算とほぼ等しいことが分かる.
最後に「大ざっぱに,入力インピーダンスはどれくらい?」を知りたいときは,式1の右辺第二項が支配的であるため「REをトランジスタの電流増幅率倍」と覚えておくと便利です.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_003.zip
●データ・ファイル内容
Bipolar_CC_Zin.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










