電圧源回路と等価な電流源回路

電圧源を使用した回路は,電流源を使用して,まったく等価な回路に置き換えることができます.図1の点線内の回路は,出力電圧が1.5V,出力抵抗が100Ωの電源です.1.5Vの直流電圧源(V1)に100Ωの抵抗(R1)が直列に接続され,その抵抗を介して負荷抵抗(RL)が接続されています.図1とまったく等価な働きをする電流源を使用した回路は,図2の(A)~(D)のどれでしょうか.
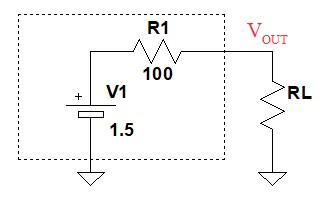
点線内は出力電圧が1.5V,出力抵抗が100Ωの電源.
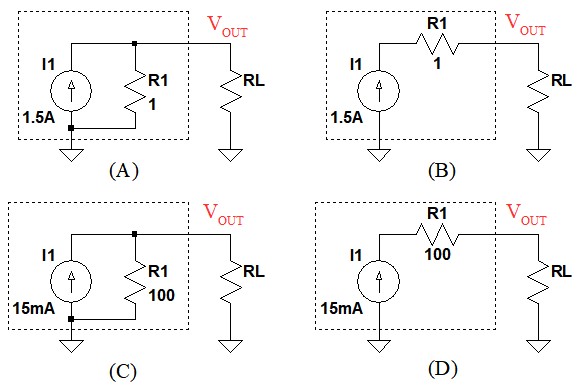
図1とまったく等価な回路はどれ?
図1の回路と等価な働きをする回路とは,負荷抵抗(RL)の値を変えた場合でも,RLに加わる電圧やRLに流れる電流が,図1と同じになる回路のことです.無負荷時(RL=∞のとき)の出力電圧(VOUT)と,RLが100ΩのときのVOUTを計算して比較すれば,簡単に答えが分かります.
図1の回路の無負荷時(RL=∞のとき)の出力電圧(VOUT)は1.5Vです.また,RLの値が100ΩのときのVOUTは0.75Vになります.図2の(A)~(D)の中で無負荷時の出力電圧が1.5Vになるのは,(A)と(C)なので,正解は(A)か(C)のどちらかです.次に,RLが100ΩのときのVOUTを計算すると(A)が約1.5Vで(C)が0.75Vになります.つまり,図1と等価な働きをするのは(C)ということになります.
●電圧源を使用した回路の負荷抵抗値と出力電圧の関係
まず,図1の回路の負荷抵抗の値と出力電圧の関係が,どのようになっているか計算してみます.図1の回路の出力電圧(VOUT)は,V1をR1とRLで分圧したものなので,式1で計算することができます.
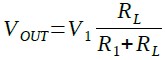 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
無負荷時(RL=∞)の出力電圧は式2のようにV1と同じ1.5Vになります.
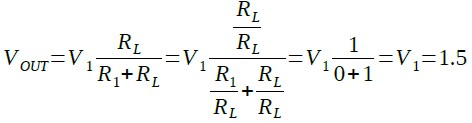 (RL=∞)・・・・・・・(2)
(RL=∞)・・・・・・・(2)
負荷抵抗の値が100Ωのとき(RL=R1)の出力電圧は式3のようにV1の半分の0.75Vになります.
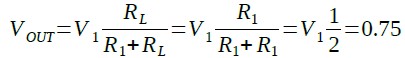 (RL=R1)・・・・・・・・・・・(3)
(RL=R1)・・・・・・・・・・・(3)
●電流源とR1が並列接続された回路の負荷抵抗値と出力電圧の関係
次に,図2の(A)と(C)の回路の負荷抵抗の値と出力電圧の関係が,どのようになっているか計算してみます.(A)と(C)の回路は,R1とRLの並列回路に電流源I1の電流が流れることになります.したがって,出力電圧(VOUT)は,R1とRLの並列接続抵抗値に電流I1を掛け合わせたもので,式4となります.
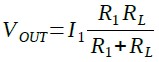 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
「I1R1=V1」となるようにV1を定義すると,式4は,式5のように変形することが可能です.式5は,式1とまったく同じになることが分かります.
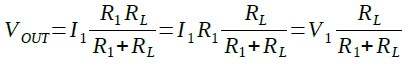 ・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・(5)
つまり,図2の(A)と(C)の回路で,I1R1の値が図1のV1と同じ値で,R1の値が図1のR1の値と等しくなっていれば,両者は全く等価な働きをします.図2の数値を代入すると,(A)と(C)の回路は共に「I1R1=1.5V」となります.一方,R1の値が図1と同じ100Ωなのは(C)なので,図1と等価な働きをするのは(C)ということが分かります.
確認のために,RLの値が100ΩのときのVOUTを計算すると,(A)のVOUTは約1.5Vで式6となります.
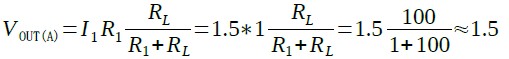 ・・・・・・・・(6)
・・・・・・・・(6)
(C)のVOUTは,式7のように0.75Vになります.
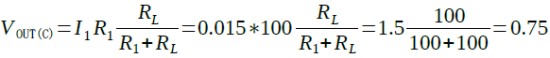 ・・・・・(7)
・・・・・(7)
●電流源とR1が直列接続された回路の負荷抵抗値と出力電圧の関係
次に(B)と(D)の回路の負荷抵抗値と出力電圧の関係を考えます.(B)と(D)の回路は電流源I1とR1とRLがすべて直列になっています.そのため,負荷抵抗(RL)に流れる電流はI1と同じ値になり,出力電圧(VOUT)は式8で計算することができます.
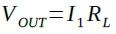 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式8を見ると分かるように,(B)と(D)の回路の無負荷時(RL=∞)の出力電圧は無限大となってしまいます.また,RLが100ΩのときのVOUTを計算すると(B)のVOUTは150Vで式9となります.
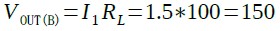 ・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・(9)
(D)のVOUTは,式10のように1.5Vになります.
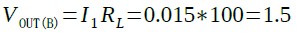 ・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・(10)
●電圧源回路と電流源回路の等価変換
式5と式1が同じ形となることから分かるように,図3のような電圧源回路と電流源回路は,相互に等価変換することができます.それぞれの回路の抵抗値を,同じ値とし,電圧源回路を電流源回路に変換するときは「I=V/R」とします.また,電流源回路を電圧源回路に変換するときは「V=I*R」とします.
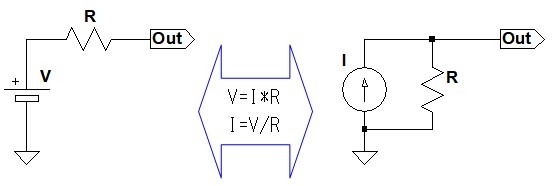
I=V/RまたはV=I*Rとすることで,相互に変換することができる.
●負荷抵抗値と出力電圧の関係をシミュレーションする
図4は,図1と図2の回路をシミュレーションするための回路です.同時にシミュレーションできるよう,すべての回路を一枚の回路図にまとめています.これらの回路で負荷抵抗RLの値を変えてVOUTの値をシミュレーションします.負荷抵抗の値はRという変数にして「.step」コマンドで変化させます.
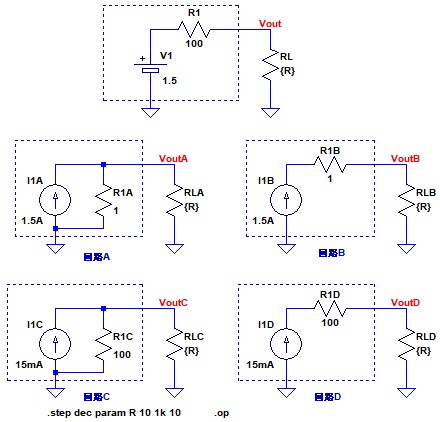
「.step」コマンドで抵抗値を10Ωから1kΩまで一桁あたり10ポイントで変える.
「.step」コマンドを入力するときは,LTspiceの補助機能を利用すると便利です.まず「.op」アイコンをクリックして図5のような編集画面を表示させ,エディット領域を右クリックしてメニューを表示します.そのメニューから「Help me Edit」,「.step Command」を選択します.
エディット領域を右クリックしてメニューを表示する.
すると,図6のような「.step」コマンドを編集するための画面が表示されるので,スイープする変数名やスイープの方法,開始値,終了値,ステップ数を入力します.今回はRという変数を10から1kまで一桁あたり10ポイントで変化させます.
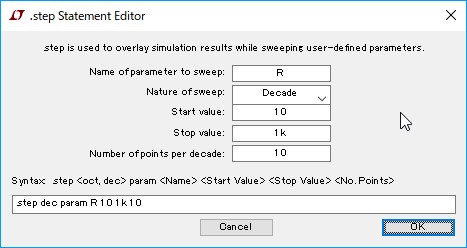
Rという変数を10から1kまで一桁あたり10ポイントで変化させる.
図7が図4のシミュレーション結果です.横軸は対数目盛としてあります.最上段が電圧源を使用した回路のVOUTの値です.2段目が電流源を使用した回路(A)と回路(C)のVOUTの値ですが,回路(C)のシミュレーション結果は,電圧源を使用した回路のシミュレーション結果と完全に一致していることが分かります. 回路(A)はR1が1Ωとなっており,出力抵抗が小さいためVOUTはRLの値によらず,ほぼ1.5Vとなっています.3段目,4段目は回路(B)と回路(D)ですが,図1の回路とはまったく異なった結果となっています.
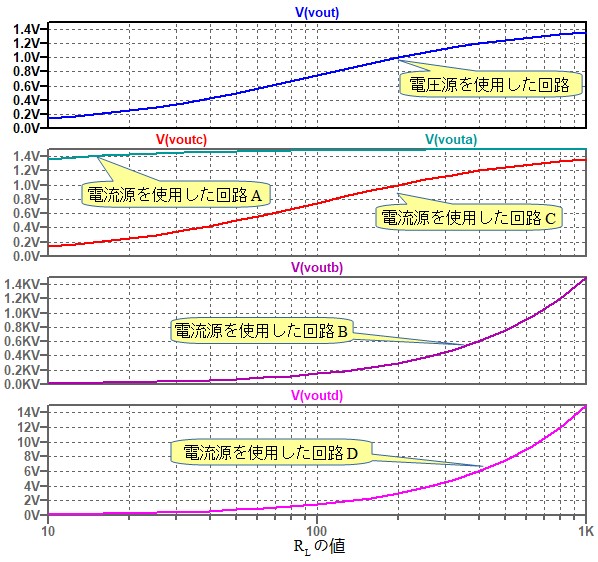
電流源を使用した回路(C)は,電圧源を使用した回路と完全に一致.
以上,電圧源回路と電流源回路の等価変換について解説しました.複雑な回路の動作を理解するとき,電流源回路を電圧源回路に変換すると,直観的に理解しやすくなることがあります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_002.zip
●データ・ファイル内容
RL_Vout.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










