キルヒホッフ法則で抵抗値を求める

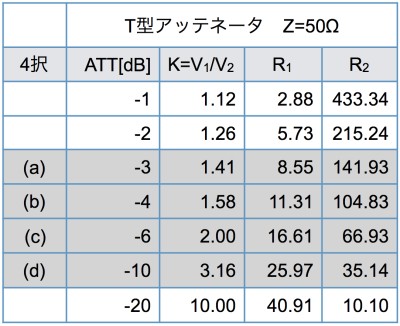
図1の破線内は,50Ωで整合をとったT型アッテネータ(減衰器)です.IN端子からOUT端子の直列に接続した2つの抵抗(R1)は同じ抵抗値です.また,ノードAからGND間に抵抗(R2)がT字に接続されています.この回路において,IN端子から右側をみたインピーダンスが50Ωで,VOUT/VINの減衰が-10dBとなる抵抗値の組み合わせは,(a)~(d)のどれでしょうか.
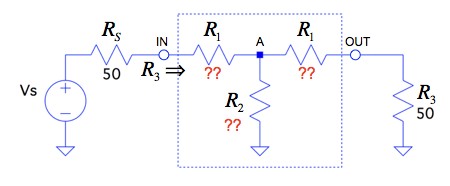
(b)R1=11.31Ω,R2=104.83Ω
(c)R1=16.61Ω,R2=66.93Ω
(d)R1=25.97Ω,R2=35.14Ω
今回は,キルヒホッフ法則の電流則(第一法則)と電圧則(第二法則)で,T型アッテネータの抵抗値を計算します.図1の回路は50Ωで整合をとるため,IN端子から右側の抵抗ネットワークのインピーダンスは,R3と同じ抵抗値の50Ωでなければなりません.IN端子の電圧は「IN端子から流れ込む電流×50Ω」で,OUT端子の電圧は「OUT端子から流れ出る電流×50Ω」なので,アッテネータのVOUT/VINの減衰は,この2つの電流比によって決まります.
アッテネータの減衰を1/Kとすれば,Kは式1で求められます.
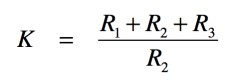 ・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
IN端子から右側をみたインピーダンスは,式2となります.
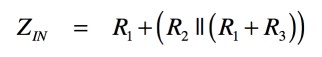 ・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・(2)
式1と式2を使って,(a)~(d)についてアッテネータの減衰とIN端子からみたインピーダンスは,次のようになり,答えは(d)となります.
| (a)R1= 8.55Ω,R2=141.93Ω,R3=50Ω: | 20log10(K-1)=-2.99dB,ZIN=50.00Ω |
| (b)R1=11.31Ω,R2=104.83Ω,R3=50Ω: | 20log10(K-1)=-3.99dB,ZIN=49.99Ω |
| (c)R1=16.61Ω,R2=66.93Ω,R3=50Ω: | 20log10(K-1)=-5.99dB,ZIN=49.99Ω |
| (d)R1=25.97Ω,R2=35.14Ω,R3=50Ω: | 20log10(K-1)=-9.99dB,ZIN=49.99Ω |
●キルヒホッフの法則について
回路を解析するときに重要なのは,回路内の電圧と電流の値とその方向です.これらを規定するのがキルヒホッフの法則でオームの法則と同様によく使われます. 図2はキルヒホッフの法則の説明図です.
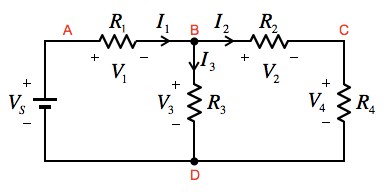
図2において,回路のノード(節点)を1回だけ通り,元に戻るループを閉路(または閉ループ,クローズループ)といい,この閉路に,電圧源や電流源,抵抗,コンデンサ,インダクタなどがあります.図2の1つの閉路を例にとると,ノードの記号で「A→B→D→A」という閉路に電圧源(VS)と抵抗(R1,R3)があります.回路では,いくつかの閉路について,以下の2つのキルヒホッフの法則が成り立ちます.
キルヒホッフの電流則(第一法則)
回路内のある1つのノードに流れ込む電流の総和はゼロである
キルヒホッフの電圧則(第二法則)
回路内の閉路において枝電圧の総和はゼロである
キルヒホッフの電流則を図2で解説すると,Bのノードに流れ込む,または,流れ出す電流値とその方向の規定です.BのノードにはI1が流れ込み,I2とI3が流れ出します.よって,式3の関係が導かれます.
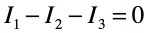 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
次にキルヒホッフの電圧則ですが,図2中の「A→B→D→A」の閉路は式4になります.
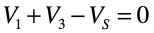 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
また「B→C→D→B」の閉路は式5となります.
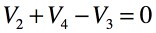 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
以上のように,回路内の電圧と電流,また,その方向より回路方程式をたてて,回路の解析を行います.なお,これ以降,キルヒホッフの電流則を「KCL」,キルヒホッフの電圧則を「KVL」と記述します.
●KCLとKVLを使い抵抗値を求める
ここでは,図3の50Ωで整合をとったT型アッテネータについて,KCL,KVLを使って回路の方程式を立て,R1とR2の抵抗値を導きます.50Ωで整合をとるため,V1とV2のノードから左右のインピーダンスを見たとき,R3と同じ抵抗値の50Ωでなければなりません.V1とV2の電圧は,オームの法則より「V1=I1R3」,「V2=I2R3」となります.R3の抵抗値が同じですから,アッテネータの減衰(VOUT/VIN)は,IOUT/IINの電流比で決まることになります.
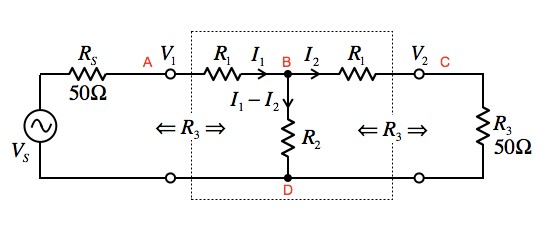
V1,V2のノードから左右のインピーダンスをみると,R3(=50Ω)となるようにR1とR2を選ぶ.
BノードのKCLより,式6が導けます.
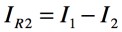 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
また,式6を使い「B→C→D→B」の閉路のKVLより,式7の電圧の関係があります.
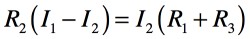 ・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7を整理してI1とI2の電流比を求めると,式8となります.これが式1の出所です.
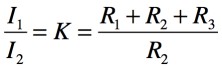 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
次にV1から右側を見たインピーダンスの計算をします.このインピーダンスは50Ω(=R3)と同じにすることから,式9となります.
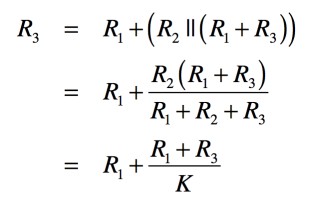 ・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・(9)
式9を整理すると,式10となり,R1とR3の関係になります.
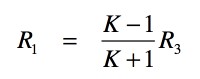 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
R2を求めるため,式8へ式10を代入すると,式11となります.
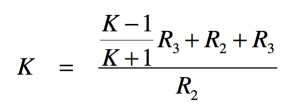 ・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・(11)
式11を整理すると,式12となり,R2とR3の関係求められました.
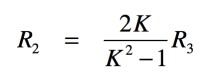 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
式10と式12を使いR3が50Ωのとき,アッテネータの減衰毎にR1とR2を求めたのが表1となります.問題の(a),(b),(c)は,-3dB,-4dB,-6dBのときのR1とR2の抵抗値となります.
●T型アッテネータをLTspiceで確かめる
図4は,図1の回路で(a)~(d)の条件についてシミュレーションする回路です.
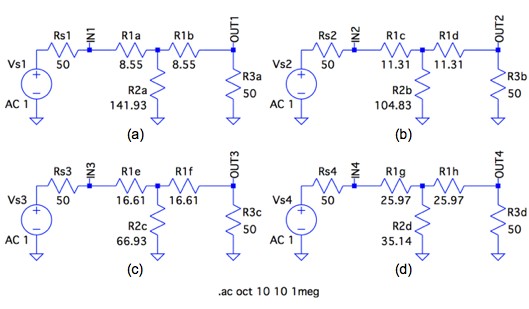
(a)~(d)の抵抗値についてVOUT/VINの減衰とIN端子から右側のインピーダンスを調べる.
この4つの回路ごとにVOUT/VINの減衰をプロットした結果が図5です.図5より,(a)~(d)は,表1の「ATT」の列にある減衰と同じ結果で,目標とした設計値とシミュレーション値は一致しています.
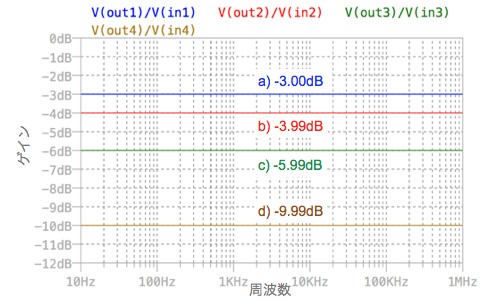
表1の減衰と同じ結果となる.
また,IN端子から右側のインピーダンスをプロットしたものが図6となります.IN端子から右側をみたインピーダンスも,4つの回路全てにおいて,目標とした50Ωとなっていることがわかります. このようにT型アッテネータの抵抗(R1,R2)を適切に調整することにより,アッテネータの減衰をコントロールできます.
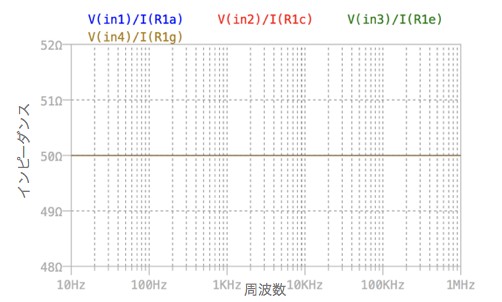
4つの回路とも,インピーダンスは50Ωとなる.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice4_001.zip
●データ・ファイル内容
T_type_attenuator.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










