発火させないためのチップ温度と熱抵抗

図1は,NチャンネルMOSトランジスタを使用した簡易シリーズ・レギュレータです.回路定数は,入力電圧が50V,出力電圧が約12V,負荷抵抗が120Ωとなっています.
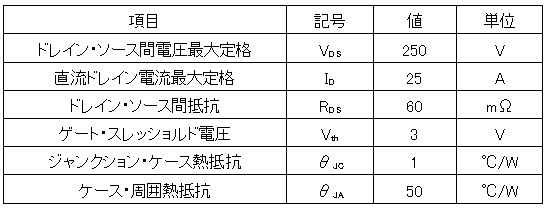
この条件の場合,MOSトランジスタ(M1)のチップの温度(Tj:ジャンクション温度)は,計算上(A)~(D)の何℃になるでしょう?ただし,MOSトランジスタの概略仕様は表1とし,周囲温度は25℃とします.
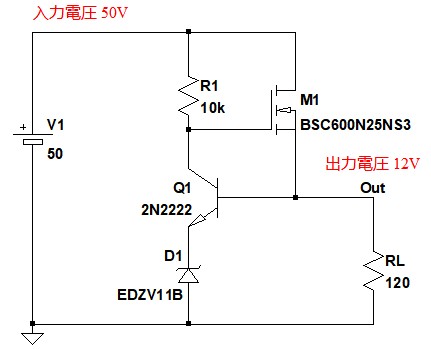
MOSトランジスタ(M1)のチップの温度は何℃になるか?
チップの温度(ジャンクション温度)を計算するためには,MOSトランジスタ(M1)の消費電力を求める必要があります.まず,出力電圧と負荷抵抗の値から出力電流を計算し,次にMOSトランジスタの消費電力を計算します.MOSトランジスタの消費電力が分かれば,熱抵抗を使用してジャンクション温度(チップの温度)を計算することができます.
図1でM1のドレイン・ソース間電圧は,入力電圧と出力電圧の差なので「50-12=38V」です.一方,出力電流は「12V/120Ω=0.1A」で,これがM1のドレイン電流になります.つまり,M1の消費電力は3.8Wです.さらに,M1のジャンクションと周囲熱抵抗が51℃/Wなので,チップ温度は「TJ=3.8*51+25=219℃」となります.つまり,正解は(D)ということになります.
●熱抵抗を使用してジャンクション温度を計算する
半導体の仕様書に記載されているパッケージの熱抵抗とその半導体の消費電力が分かれば,半導体チップの温度を計算することができます.チップ温度のことを一般的にジャンクション温度と呼んでいます.なので,以後はジャンクション温度と表記します.
まず,図1のMOSトランジスタ(M1)の消費電力を計算します.M1の消費電力はドレイン・ソース間電圧にドレイン電流を乗じたものです.ここで,図1の出力電圧は12Vで負荷抵抗が120Ωですから,ドレイン電流は式1のように0.1Aと計算できます.
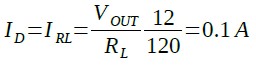 ・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また,M1の消費電力PM1は式(2)で計算することができます.
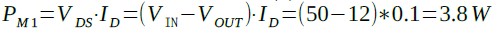 ・・・・・・・・・(2)
・・・・・・・・・(2)
表1の仕様書を見ると,M1のジャンクションとケース熱抵抗(θJC)は1℃/Wです.これはジャンクションとケース表面までの熱抵抗です.また同様にM1のケースと周囲熱抵抗(θCA)は,50℃/Wです.これは,ケースと周囲環境までの熱抵抗です.ジャンクションから周囲環境までの熱抵抗は(θJC)と(θCA)を足したものです.周囲温度(Ta)を25℃とすると,ジャンクション温度(TJ)は,式3で計算することができます.
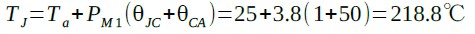 ・・・・・・・・・・(3)
・・・・・・・・・・(3)
式3の計算結果より,図1のMOSトランジスタ(M1)のジャンクション温度は,約220℃となります.
●熱抵抗はシミュレーションできる
図2は,図1の「熱抵抗を電気抵抗」,「消費電力を電流」,「温度を電圧」に置き換え,ジャンクション温度を,LTspiceでシミュレーションするための回路です.「.op」のシミュレーション結果を回路図上に表示してあります.端子Tjの電圧は218.8Vとなり,これはTjが218.8℃になることを意味しています.

消費電力を電流に置き換え,温度は電圧に置きかえる.
●放熱器をつけたジャンクション温度をシミュレーションする
一般的に半導体製品は,ジャンクション温度が150℃以下になるようにして使用しないと,破壊してしまう危険性があります.図1の回路はそのままではジャンクション温度が150℃を大きくこえてしまっているため,放熱器をつけてジャンクション温度を下げる必要があります.
放熱器の熱抵抗(θfa)が分かれば,半導体に放熱器を取り付けた場合のジャンクション温度を計算することができます.図3は,熱抵抗(θfa)10℃/Wの放熱器を追加したときの熱抵抗等価回路です.Tjのシミュレーション結果も表示していますが,放熱器をつけることでジャンクション温度が60℃に下がることが分かります.

放熱器をつけることでジャンクション温度が60℃に下がっている.
●LTspice付属のMOS熱解析モデルを使用する
図2や図3は,MOSトランジスタの消費電力を手計算し,熱抵抗を電気抵抗に置き換えた熱シミュレーション用の等価回路です.LTspiceにはこのような等価回路図を作らずに熱シミュレーションを行うことができるモデルが用意されています.図4が「SOAtherm-NMOS」という名前のMOSトランジスタの熱解析用シンボルです.図4ではBSC600N25NS3というトランジスタ用のモデルになっています.このシンボルを右クリックして別のトランジスタ用のモデルに置き換えることができます.なお,このシンボルはパッケージの熱モデルです.図4でMOSトランジスタの絵柄が破線になっています.また,このシンボルの上に,MOSトランジスタのシンボルを重ねて配置することで,電気的なシミュレーションができるようになります.
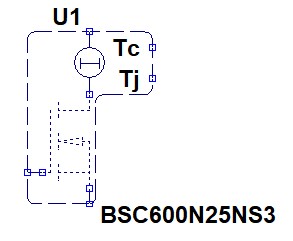
パッケージの熱モデルなので,別にMOSトランジスタのシンボルを重ねて配置する.
この熱解析用のモデルを使用すると,トランジスタの消費電力に対応したジャンクション温度の値だけではなく,ジャンクション温度の時間的変化もシミュレーションすることができます.
●シリーズ・レギュレータのジャンクション温度をシミュレーションする
図5は,図1の回路を熱解析モデルを使用して書き換えたものです.電源(V1)を0Vから50Vに立ち上げた後,ジャンクション温度がどのように変化するかをシミュレーションします.なお,周囲温度を25℃としてシミュレーションするため「Tambient=25」と設定しています.
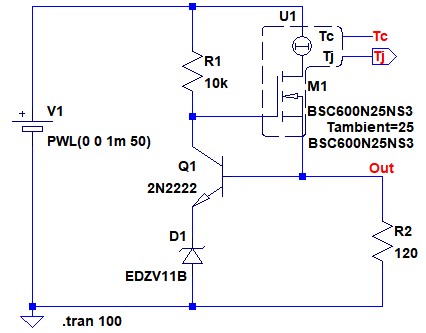
Tjという名前のノード電圧がジャンクション温度を表す.
図6が図5のシミュレーション結果です.青線がジャンクション温度で赤線がパッケージ表面温度です.縦軸は電圧目盛となっていますが,この電圧を温度と読み替えます.電源立ち上げ後,5秒程度でジャンクション温度(V(tj))は218℃になることがわかります.この値は式3で計算した値と同じです.またパッケージ表面の温度はジャンクション温度よりも6℃ほど低くなっています.
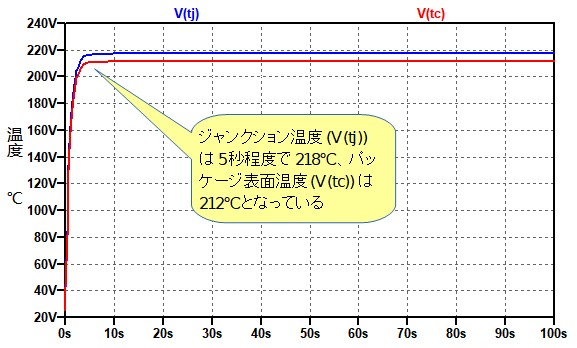
ジャンクション温度(V(tj))は5秒程度で218℃になる.
●放熱器モデルを使用してジャンクション温度をシミュレーションする
図7は,図5の回路に放熱器熱解析モデル(SOAtherm-HeatSink)を追加したものです.Tambientパラメータで周囲温度を25℃と指定しています.熱抵抗はRthetaというパラメータで指定し,図3と同じ10W/℃となっています.「Area_Contact_mm2」というパラメータはデバイスとの接触面積で,Volume_mm3は,ヒートシンクの体積を表し,いずれもディフォルト値のままとしています.BSC600N25NS3というMOSトランジスタの外形寸法を考慮すると,これらは実際にはもう少し小さな値とする必要があります.SOAtherm-HeatSinkを回路図に配置したら,そのTc端子とNMOS熱解析モデル(SOAtherm-NMOS)のTc端子を配線で接続します.
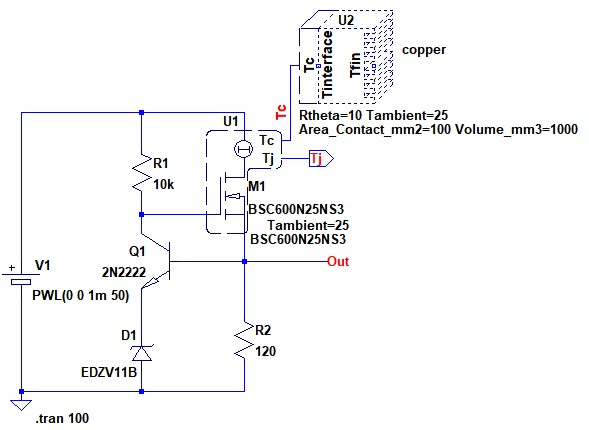
放熱器の熱抵抗はパラメータRthetaで指定し,10W/℃となっている.
図8は,図7のシミュレーション結果です.放熱器を付けることでジャンクション温度の変化が緩やかになっています.100秒程度で温度上昇は落ち着き,64℃と放熱器がないときにくらべ,大幅に低くなっています.
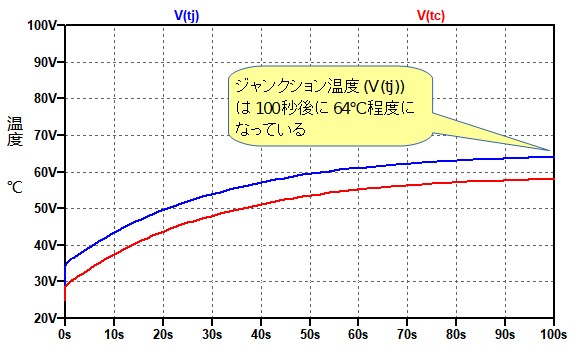
ジャンクション温度は100秒後に64℃程度になっている.
以上,熱抵抗とジャンクション温度の関係を解説しましたが,LTspiceの熱解析モデルを使用すると,より実際的な発熱のシミュレーションが行えます.今回はシリーズ・レギュレータという,消費電力が一定の回路でシミュレーションを行いました.LTspiceの熱解析モデルを使用すれば,手計算では困難な,パルス状に複雑に消費電力が変化する回路の,温度上昇のシミュレーションを行うことができます.ぜひ活用してみてください.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice3_044.zip
●データ・ファイル内容
TJ.asc:図2の回路
TJ_HT.asc:図3の回路
S_reg.asc:図5の回路
S_reg_HT.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










