温度変化に強い固定電圧レギュレータ

図1は,バンドギャップ・リファレンス回路を用いた,固定電圧レギュレータです.図のNPNトランジスタは,Q2が8倍(2N2222を並列に8個接続),その他は全て1倍(1個)です.トランジスタのベース-エミッタ電圧はQ3が592mVで,Q4,Q5,Q6のベース-エミッタ電圧は,流れる電流が同じなので全て606mVとなります.NチャネルJFET(J1)と抵抗(R5)は,約100μAの定電流源です.この固定電圧レギュレータにおいて,Vreg端子の出力電圧は(a)~(d)のうちどれでしょうか.
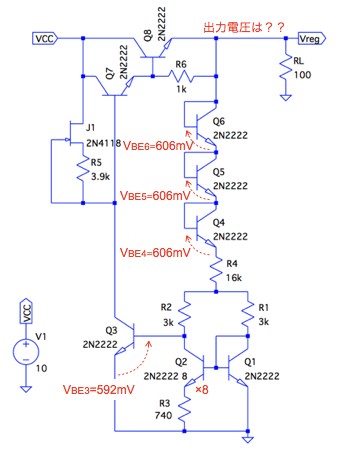
回路定数とベース-エミッタ電圧を使い,Vreg端子の電圧を計算する.
トランジスタの熱電圧(VT)は26mVとし,計算を簡単にするため,トランジスタの電流増幅率(hFE)は無限大で考え,ベース電流は無視します.
今回は,バンドギャップ・リファレンスの応用回路である,固定電圧レギュレータについて解説します.トランジスタQ1とQ2の比は1:8の関係と抵抗(R3)より,抵抗(R2)に流れる電流が求められます.この電流値より,R2とR4の電圧降下を求め,図1のNPNトランジスタのベース-エミッタ電圧より,出力端子の電圧(Vreg)が求められます.
図1の固定電圧レギュレータは,温度に対して安定した出力電圧を供給できます.素子数も少ないため,モノリシック集積回路の簡易的なシリーズ電源回路として使われます.同じ回路でトポロジーの固定電圧レギュレータは数多くあります.
図1の回路において,抵抗(R3)の両端にかかる電圧は,NPNトランジスタQ1とQ2のベース-エミッタ電圧差(VBE1-VBE2)となります.よって,抵抗(R3)に流れる電流は,式1となります.
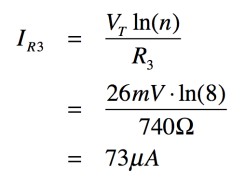 ・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
バンドギャップ・リファレンスは,R1とR2に流れる電流(IR1,IR2)が等しくなるときに落ち着きます.出力電圧(Vreg)は,トランジスタ(Q3,Q4,Q5,Q6)のベース-エミッタ電圧と,抵抗(R2,R4)の電圧降下の総和ですので,式1の電流値を用いると,式2となります.よって図1は,約5Vの固定電圧レギュレータとして動作します.
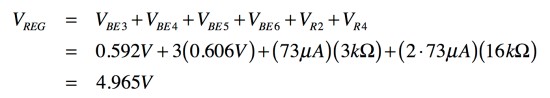 ・・・・・(2)
・・・・・(2)
●固定電圧レギュレータについて
図1の固定電圧レギュレータの定性的な回路動作から解説します.固定電圧レギュレータの出力電圧は,Q1,Q2,Q3,R1,R2,R3からなるバンドギャップ・リファレンスの電圧にQ4,Q5,Q6,R4の電圧分を加えた電圧となります.Q8は,出力パス・トランジスタでありQ7とR6はそのドライバです.J1,R5は定電流源であり,その電流の一部はQ7のベース電流,残りはQ3のコレクタ電流となります.また,RLは,固定電圧レギュレータの負荷抵抗です.
電源電圧(V1)が0Vから増加すると,R2に流れる電流(IR2)よりQ2のコレクタ電流(IC2)が多い(IR2<IC2)ため,Q3はOFFとなり,出力パス・トランジスタ(Q8)が導通して出力電圧(Vreg)は増加します.これは,Q1,Q2,R3からなるワイドラー・カレント・ミラー回路は,トランジスタに流れる電流が少ないと,R3の電圧降下は小さく,Q1,Q2のトランジスタの比が優位となり,R2に流れる電流よりも,Q2のコレクタ電流の方が多いことによります.入力電圧の増加とともに出力電圧も増加し,R2に流れる電流がQ2のコレクタ電流より多くなると,Q3はオンして出力パス・トランジスタ(Q8)の導通を抑制します.この負帰還により,出力電圧(Vreg)は一定となります.
出力電圧(Vreg)の温度特性は,トランジスタ(Q3,Q4,Q5,Q6)の負の温度係数であるベース-エミッタ電圧を,抵抗(R3)の正の温度係数となる電圧降下で温度補償します.
●出力電圧の一般式を計算する
解答では具体的な数値で計算しましたが,ここでは図1の記号を使い,出力電圧(Vreg)の一般式を導きます.なお,トランジスタの電流増幅率(hFE)は無限大とし,ベース電流は無視します.
負帰還がかかり,出力電圧が定電圧となるとQ1,Q3のベース電圧は,ほぼ同じになり,よって,抵抗R1とR2の両端の電圧も同じになります.これより,Q1コレクタ電流(IC1),Q2コレクタ電流(IC2),抵抗R1とR2の関係は式3となります.
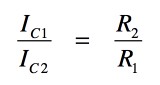 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
トランジスタQ1とQ2の倍率を「Q1:Q2=1:n」とすると,抵抗(R3)の両端の電圧(VR3)は式4となります.
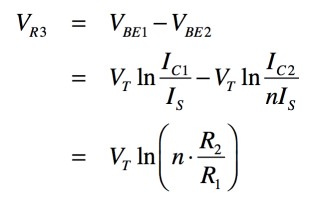 ・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・(4)
式4を使い,抵抗(R3)に流れる電流(IR3)を求めると,式5となります.
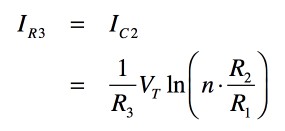 ・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・(5)
抵抗(R2)の電圧降下(VR2)は,式5を用いると,式6となります.
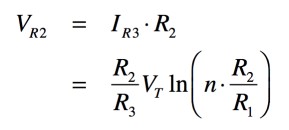 ・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・(6)
次に,抵抗(R4)の電流(IR4)を求めると式7となります.
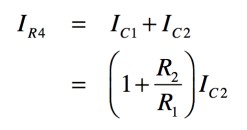 ・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
抵抗(R4)の電圧降下(VR4)は,式5,式7を用いると,式8となります.
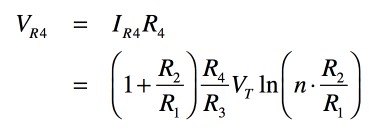 ・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・(8)
式2に示した,出力電圧(Vreg)の一般式は,式6と式8を使い,式9となります.ここで,Q4,Q5,Q6のトランジスタのベース-エミッタ電圧は,流れる電流は同じであるため,3つのベース-エミッタ電圧は等しく,「VBE4=VBE5=VBE6=VBE」としました.
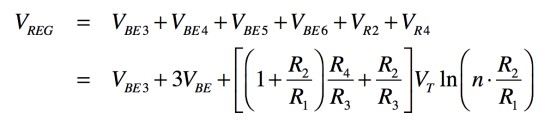 ・・・・・(9)
・・・・・(9)
式9へ回路定数を代入すると式10となり,解答(c)の5Vであることが分かります.
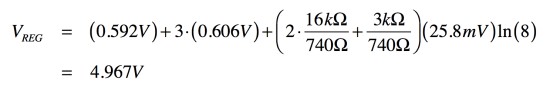 ・・・・・(10)
・・・・・(10)
●出力電圧を温度補償する抵抗値
式9に示した出力電圧(Vreg)は,トランジスタのベース-エミッタの電圧の負の温度係数と,熱温度(VT=kT/q)に関する正の温度係数となります.これより熱温度に関する項を調整し,ベース-エミッタの電圧の負の温度係数を打ち消すことにより,温度補償をします.出力電圧の式9を温度「T」で微分すると式11となります.
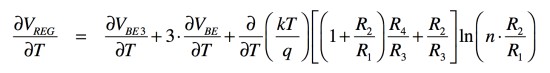 ・・・・・(11)
・・・・・(11)
温度補償することは,「∂VREG/∂T=0」とすることですので,式11の左辺をゼロとし,R3で解いて回路定数を入れると式12となります.
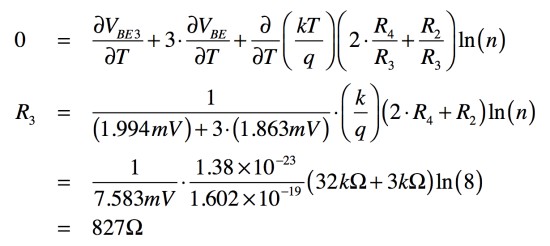 ・・・・・(12)
・・・・・(12)
ここで,VBE3の温度係数(∂VBE3/∂T)は「-1.994mV/℃」,VBEの温度係数(∂VBE/∂T)は「-1.863mV/℃」,kはボルツマン定数(1.38×10-23),qは電子電荷(1.602×10-19)です.以上より,トランジスタを理想としたときの抵抗(R3)は,式12の827Ωとなります.
●固定電圧レギュレータのシミュレーション
図2は,図1の電源電圧-出力電圧の温度特性をシミュレーションする回路です.式12で求めた抵抗(R3)は,トランジスタを理想とした計算です.トランジスタのデバイスモデルを使うと,R3の抵抗値は計算値と差が出ますので,ここでは「.step」コマンドを使い,R3の抵抗値を700Ω~800Ωを20Ωステップで可変します.温度変化は .dcコマンドで-20℃~100℃間を1℃ステップで解析し,出力電圧をプロットします.
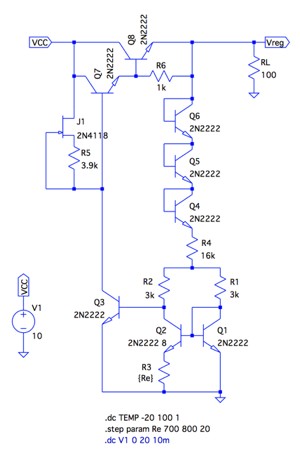
R3の抵抗値を変数Reとし,700Ω~800Ωを20Ωステップで変化させる.
図3は図2のシミュレーション結果です.R3が700Ωでは,正の温度係数が強く,800Ωでは負の温度係数が強く出ています.このようにR3を調整することにより,式11の熱電圧(VT=kT/q)に関する項を調整し,温度補償する様子がわかります.図3より,R3の抵抗値は740Ωが最適な回路定数であると考えられます.
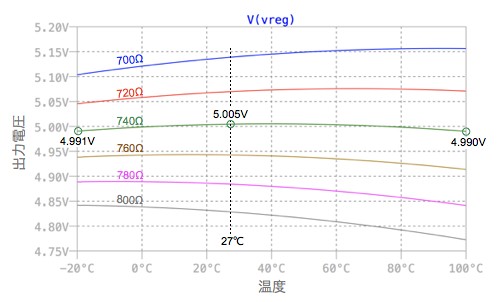
R3を740Ωに設定すると,出力電圧は温度補償できる.
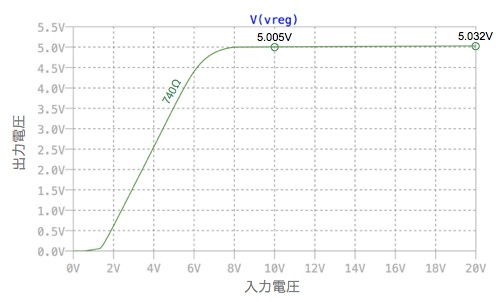
次に,図2の解析を「.dc V1 0 20 10m」へ変更し,固定電圧レギュレータの入力電圧-出力電圧をシミュレーションしたのが図4となります.R3の抵抗値は740Ωをプロットしました.入力電圧が高くなっても固定電圧レギュレータの出力電圧は,ほぼ一定の定電圧になっていることがわかります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice3_041.zip
●データ・ファイル内容
5V_Regulator.asc:図2の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
(6) LTspice電源&アナログ回路入門・アーカイブs










