バンドギャップ・リファレンスの温度補償

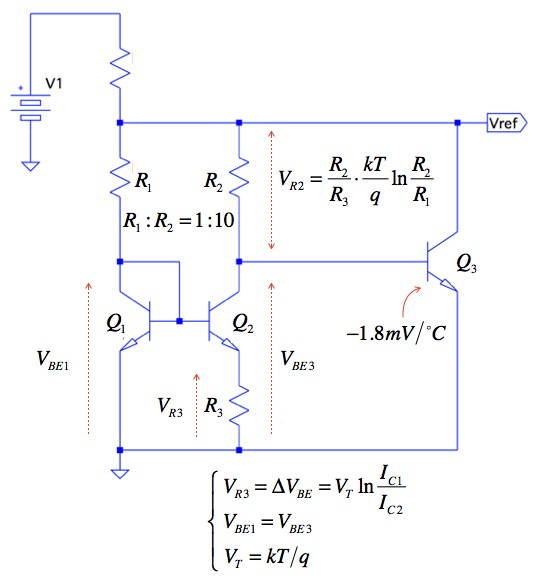
図1は,Vrefから一定の電圧を出力する,バンドギャップ・リファレンスと呼ばれる定電圧源です.この回路は,Q1,Q2,R3からなるカレント・ミラーとQ3のエミッタ接地で構成されています.回路の条件として,Q1,Q2,Q3は,同じトランジスタです.R1とR2の抵抗比は1:10です.Q1のベース・エミッタ電圧(VBE1)とQ3のベース・エミッタ電圧(VBE3)の値は同じです.また,Q3のベース・エミッタ電圧の負の温度係数は-1.8mV/℃とします.これらの関係を使い,図中に回路内の電圧を式で示しました.
Vrefの温度係数は,R3とR2の抵抗比の調整で温度補償ができます.図1において,Vrefの温度係数が最も小さいR3とR2の抵抗比は(a)~(d)のどれでしょうか. なお,計算を簡単にするため,トランジスタのベース電流はゼロ,アーリ電圧は無限大とします.
kはボルツマン定数で1.38×10-23 [J/K],qは電子電荷で1.6×10-19 [C],Tは絶対温度で27℃のとき300[K].
今回は,ワイドラーのバンドギャップ・リファレンスの温度補償について解説します.図1のVrefを式で表すと,「Vref=VBE3+VR2」です.温度係数を求めるときは,Vrefの式を温度(T)で微分したものなので,「∂Vref/∂T=∂VBE3/∂T+∂VR2/∂T」となります.Vrefを温度補償するには,温度による変化がゼロ,すなわち「∂Vref/∂T=0」とします.VBE3の負の温度係数は「∂VBE3/∂T=-1.8mV/℃」ですので,R3とR2の抵抗比を調整してVR2の正の温度係数「∂VR2/∂T=+1.8mV/℃」とすれば温度補償ができます.このときのR3とR2の抵抗比を求めます.
VBE3の負の温度係数「∂VBE3/∂T=-1.8mV/℃」をVR2の正の温度係数「∂VR2/∂T=+1.8mV/℃」で打ち消すようにR3とR2の抵抗比を調整します.図1に記載しているVR2の式より,温度係数「∂VR2/∂T」を求めると式1となります.
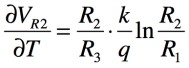 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
R1とR2の抵抗比1:10と,ボルツマン定数(k),電子電荷(q)の定数を使い,式1の左辺の「∂VR2/∂T=+1.8mV/℃」となるR3とR2の抵抗比は式2となります.
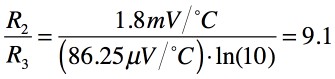 ・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・(2)
以上より,「R2/R3=9.1」となり,R3とR2の抵抗比は(d)の1:9となります.
●バンドギャップ・リファレンスの温度補償について
図2は,温度補償について解説するために,図1を書き直したものです.この図を使い,バンドギャップ・リファレンスの温度補償について解説します. 図2のバンドギャップ・リファレンスは,Q1,Q2,R3からなるカレント・ミラーとQ3のエミッタ接地で構成しています.R1とR2は,Q1とQ2に流れる電流を決める抵抗です.バンドギャップ・リファレンスの出力電圧(Vref)は,Q3のベース・エミッタ電圧(VBE3)と,R2の電圧降下(VR2)を加算した電圧となります. よって,Vrefの温度係数は,VBE3の負の温度係数を,VR2の正の温度係数で打ち消しあうように設定すれば温度補償ができます.
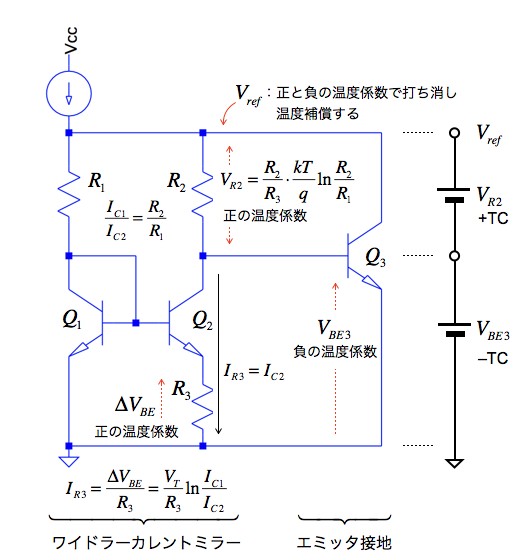
次にVR2の温度係数について詳しく解説します.VR2は,カレント・ミラー出力電流(Q2のコレクタ電流)が正の温度係数となることから,R2の電圧降下(VR2)も正の温度係数となります.具体的には,Q1とQ2のベース・エミッタ電圧が等しいとすると,2つのトランジスタに流れる電流比(IC1/IC2)は,R1とR2の抵抗比(R2/R1)と同じになります.ここでカレント・ミラーのQ2コレクタ電流はQ1コレクタ電流より小さくなる(IC1<IC2)ため,R1>R2の関係となります.
Q1とQ2に異なった電流が流れることから,2つのトランジスタのベース・エミッタ電圧差(ΔVBE)がR3に発生します.ΔVBEは正の温度係数を持つことから,R3に流れる電流が正の温度係数となり,よってR2の電圧降下も正の温度係数となります. VR2の正の温度係数は,R3とR2の抵抗比で調整ができます.
カレント・ミラーは過去のメルマガ「LTspice電源&アナログ回路入門 008 ―― ワイドラー電流源の入出力電流と抵抗値の関係」で解説しています.そちらもご参照ください.
●温度補償する抵抗比を計算する
図2の定性的な説明を元に,温度補償をするR3とR2の抵抗比を求めます.まず,Q1とQ3のベース・エミッタ電圧が等しいとおくと,Q1とQ2に流れるコレクタ電流比と,R1とR2の抵抗比の関係は式3となります.
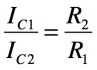 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
Q1とQ2のコレクタ電流比が違うことから,2つのベース・エミッタ電圧差(ΔVBE)は抵抗R3に発生し,式3の関係を使うと式4となります.ここで,VTは熱電圧(VT=kT/q),kはボルツマン定数,qは電子電荷,Tは絶対温度,ISはトランジスタの逆方向飽和電流です.
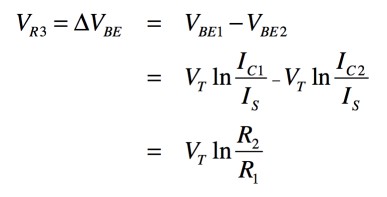 ・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・(4)
Q2のコレクタ電流(IC2)はR3に流れる電流ですので,式4の電圧をR3で割った電流です.よって,R2の電圧降下(VR2)は式5となります.
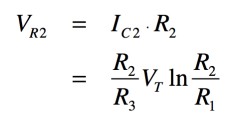 ・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
バンドギャップ・リファレンスの出力電圧(Vref)は,Q3のベース・エミッタ電圧(VBE3)と抵抗(R2)の電圧降下(VR2)を加算した電圧であり,式6となります.
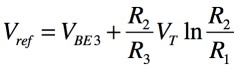 ・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
Vrefの温度係数は,式6を温度で微分して求めます.すると,式7となります.
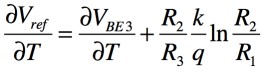 ・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7の右辺第一項はQ3のベース・エミッタ電圧の温度係数であり,冒頭の問題では-1.8mV/℃としました.また,右辺第二項はVR2の温度係数であり,これを正の温度係数+1.8mV/℃となるようにR3とR2の抵抗比を設定して打ち消します.すると,Vrefの温度係数は「∂Vref/∂T=0」となり,温度補償ができることが分かります.以上より,式7を「∂Vref/∂T=0」,「∂VBE3/∂T=-1.8mV/℃」として計算したものが式2であり,R3とR2の抵抗比は解答の1:9となります.
●温度特性をシミュレーションで確かめる
図3は,図1をシミュレーションする回路です.「R2/R1=10」とするため,R1を1kΩ,R2を10kΩとし,式2の「R2/R3=9.1」から,R3を1.1kΩとしました.R4は,Q1,Q2,Q3に十分な電流が流れるよう,2.2kΩとしています.また,全ての抵抗は+100ppm/℃の温度係数です.トランジスタ(Q1,Q2,Q3)は,2N2222を用いました.シミュレーションは,-20℃~100℃間を1℃ステップで変化させます.プロットはバンドギャップ・リファレンスの出力電圧(Vref)とQ3のベース・エミッタ電圧となるA点の電圧,また,R2の電圧降下(VR2)はVrefとA点の電圧差をプロットします.
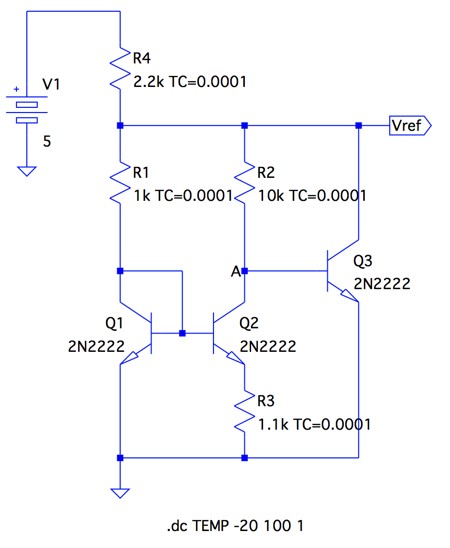
R1=1kΩ,R2=10kΩ,R3=1.1kΩ,R4=2.2kΩとした.
R2/R1=10,R2/R3=9.1としている.
図4は,図3のシミュレーション結果です.27℃でのバンドギャップ・リファレンスの出力電圧(Vref)は約1.27Vとなります.その温度係数は,27℃と37℃間で-0.43mV/℃であり,VBE3の負の温度係数-1.82mV/℃と,VR2の正の温度係数+1.39mV/℃で打ち消しあった値となります.解答の計算はトランジスタを理想としているため,シミュレーション結果は誤差が生じ,僅かに温度係数を持ちます.
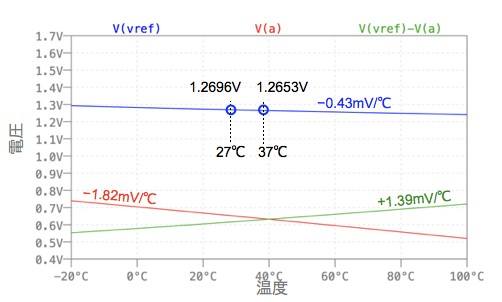
VBE3の負の温度係数とVR2の正の温度係数で打ち消しあい,Vrefの電圧は温度に対して変化が少ない.
●抵抗を変化させて出力電圧の温度変化を調べる
図4のシミュレーション結果より,VR2の温度係数が小さいため,Vrefの温度係数が-0.43mV/℃となります.そこで,VR2の温度係数を僅かに増やす目的でR3を小さくし,Vrefの温度係数を微調整するシミュレーションをします.図5は,R3を900Ωから850Ω間を10Ωステップで減少させ,Vrefの温度特性を調べる回路です.
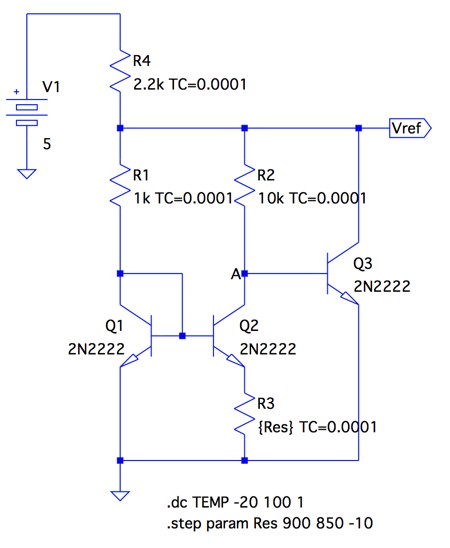
図6は,図5のシミュレーション結果で,R3を微調整すると870Ωのとき温度係数が小さくなることが分かります.
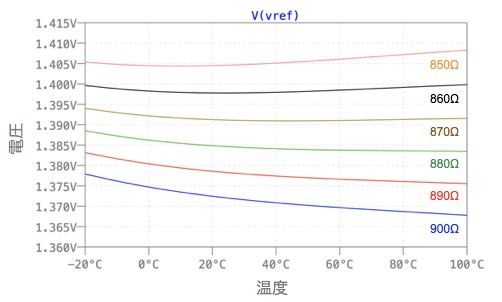
R3が870Ωのとき,Vrefの温度係数は小さくなることが分かる.
以上がバンドギャップ・リファレンスの温度補償です.リニア・レギュレータなどのシリコンへ集積化した回路では,Q1とQ2のコレクタ電流比をトランジスタのエミッタ面積で調整しています.温度補償は電流比や抵抗比を使って調整しますので,1チップへ集積化した隣り合う素子のミスマッチは小さいことを利用すれば,集積回路に適した回路といえます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice3_017.zip
●データ・ファイル内容
Widlar_BGR_1.asc:図3の回路
Widlar_BGR_2.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










