交流信号による平均電力と実効値

図1は,抵抗値が10Ωのヒータ(RH)に直流電圧10Vを加えている回路です.ヒータには1Aの電流が流れ,ヒータで発生する電力は10Wになります.このヒータに直流電圧の代わりに,図2(A)~(D)のような波形の交流電圧を加えました.(A)~(D)でヒータの発生する電力の平均値(実効値)が直流電圧と同じ10Wになるものはどれでしょうか.
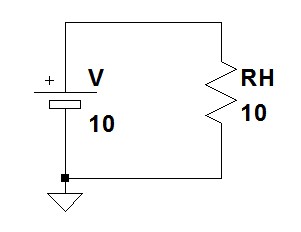
ヒータに流れる電流は1Aで,発生する電力は10W.
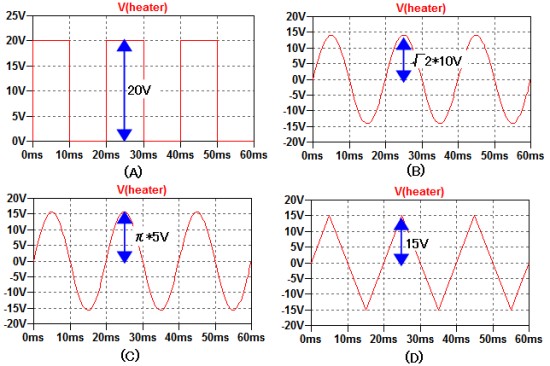
(A):ピーク電圧が20Vでデューティ比50%のパルス波
(B):振幅が√2*10Vの正弦波
(C):振幅がπ*5Vの正弦波
(D):振幅が15Vの三角波
今回は,直流電源を使用している回路を交流電源に変更した場合,負荷抵抗で発生する電力を同じにする方法を解説します.ヒータで発生する電力の瞬時値は,加えた電圧の瞬時値の二乗を抵抗値で割ったものです.この電力の瞬時値の,1周期の平均を計算すれば電力の平均値となります.これを図1の電力と比較すれば,答えが分かります.
正弦波の実効値は,ピーク値の1/√2なので,(B)の実効値は10Vとなり,抵抗で発生する平均電力は10Wになります.(A),(C)で発生する電力は10Wよりも大きく,(D)で発生する電力は10Wよりも小さくなります.
●パルス波による平均電力と実効値
まず,数式を使ってパルス波,正弦波,三角波それぞれのピーク電圧と平均電力の関係を計算してみます.図2(A)において,ピーク電圧をVPとし,周期をTとします.デューティ比50%のパルス波なので,電圧がVPとなっているT/2の期間の電力を計算し,Tの期間の電力の平均値を計算すればよいことになります.T/2の期間の電力は,VP2/RHなので,Tの期間の平均電力(PPuls)は,VP2/RHを2で割り,(1)式で計算することができます.
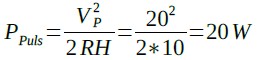 ・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・(1)
図2(A)の波形の平均電圧は,10Vなので一見,平均電力も直流10Vと同じ10Wになると思います.しかし,平均電力は,直流10Vの2倍の20Wになります.一方,実効値は,式1と同じ電力相当の直流電圧のことなので,これをVPulsRMSと置くと,式2となり,この式から式3のようにVPulsRMSを求めることができます.
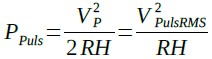 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
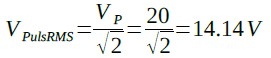 ・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・(3)
●正弦波による平均電力と実効値
図2(B)(C)の波形を,ピーク電圧をVPの正弦波(VPsin(ωt))とすると,瞬時電力は(VPsin(ωt))2/RHとなります.平均電力(Psin)は,瞬時電力を1周期分で積分し,1周期の時間で割れば求められ式4になります.
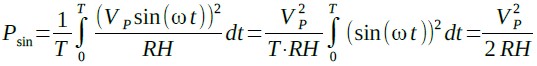 ・・・・・・(4)
・・・・・・(4)
式4に図2(B)(C)の値を代入すると,式5のように図2(B)が直流電圧10Vのときと同じ10Wとなり,式6のように図2(C)が10Wよりも大きい12.33Wとなります.
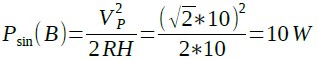 ・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・(5)
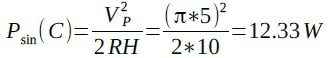 ・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・(6)
また,実効値はパルス波形のときと同様に,式4と同じ電力相当の直流電圧のことなので,これをVsinRMSと置くと式7となり,式7から式8のようにVsinRMSを求めることができます.そして,図2(B)の値を代入すると,10Vになることが分かります.
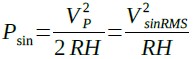 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
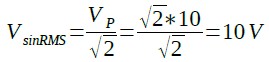 ・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・(8)
●三角波による平均電力と実効値
図2(D)の三角波の波形を見ると,1周期を4分割したそれぞれの期間の電力は同じになります.なので,平均電力は1周期の1/4の電力を積分し,1/4周期の時間で割ればよいことが分かります.最初の1/4周期の電圧は,ピーク電圧をVPとすると,4*VP*t/Tという式で表されます.そして,平均電力(Ptri)は式9で計算することができます.
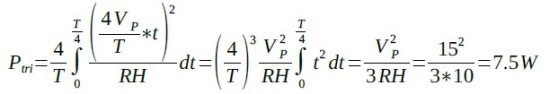 ・・・・・(9)
・・・・・(9)
実効値(VtriRMS)は,これまでと同様,式10,11で求められ,図2(D)の値を代入すると,8.66Vになります.
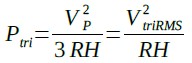 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
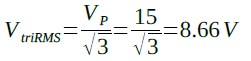 ・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・(11)
●パルス波による平均電力をLTspiceで確認する
図3は,パルス波による平均電力をシミュレーションするための回路です.ピーク電圧が20Vでデューティ比50%のパルス波となります.
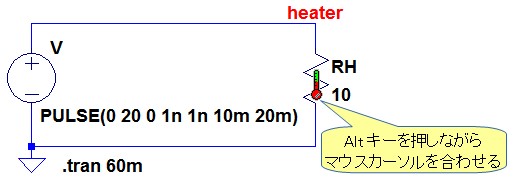
ピーク電圧20Vでデューティ比50%のパルス波.
図3でシミュレーションを実行し,Altキーを押しながら抵抗(RH)の上にカーソルを置くと,カーソルが温度計のマークに変わります.この状態で左クリックすると,図4左のようなシミュレーション結果(RHの電力波形)を表示することができます.
図4左から,ピーク電圧20Vのとき電力が40Wで,0Vのとき電力が0Wなので,平均電力が20Wになることは暗算できます.しかし,LTspiceで計算させて確認することもできます.グラフ上部のV(heater)*I(RH)をCtrlキーを押しながら左クリックすると,図4右のようなウィンドウが現れ,表示されている波形の平均値を確認することができます.
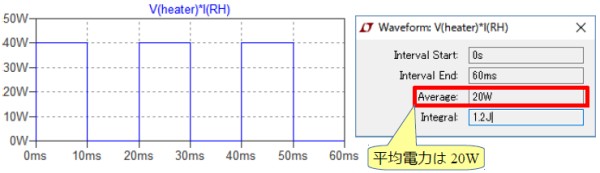
パルス電圧が20Vのときの電力は40Wで平均電力は20W.
図5左は,図3の抵抗に加わる電圧を表示したものです.ここで,V(heater)をCtrlキーを押しながら左クリックすると図5右のウィンドウで実効値が14.14Vと確認することができます.
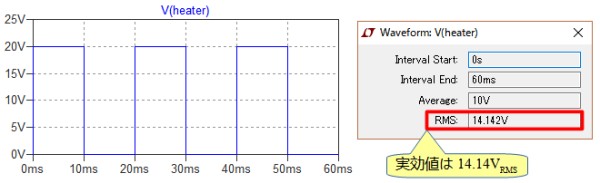
V(heater)をCtrlキーを押しながらクリックすると実効値を確認できる.
●正弦波による平均電力をLTspiceで確認する
図6は,正弦波による平均電力をシミュレーションするための回路です.正弦波の振幅は図2(B)の値(√2*10)になっています.

振幅は図2(B)の値の√2*10Vとなっている.
図7左は,図6のシミュレーション結果です.図6でAltキーを押しながら抵抗(RH)の上で左クリックし,抵抗の電力を表示しています.電力の最大値は20Wで,電力の波形は入力電圧の2倍の周波数の正弦波となっています.そして,平均電力は式5で計算したように10W(図7右)となっています.
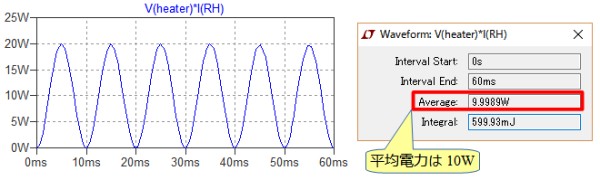
電力の最大値が20Wで平均電力は10W.
図8左は,抵抗に加わる電圧で,V(heater)をCtrlキーを押しながら左クリックして表示されたウィンドウ(図8右)から,実効値が10VRMSであることが確認できます.
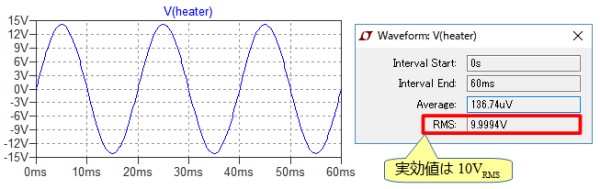
実効値は10Vとなっていることを確認できる.
図9左は,入力正弦波の振幅を図2(C)のπ*5Vにしたときのシミュレーション結果です.電力の最大値は,約25Wで平均電力は式6で計算したように12.3W(図9右)になっています.
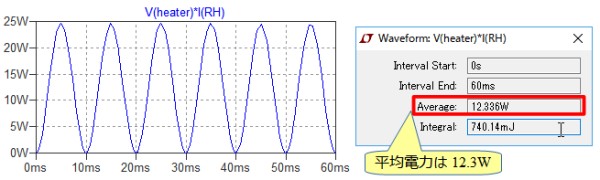
平均電力は,12.3Wになっている.
●三角波による平均電力をLTspiceで確認する
図10は,三角波による平均電力をシミュレーションするための回路です.PWL信号を使用し,各時間の電圧を指定することで三角波を生成しています.

PWL信号を使用して三角波を生成している.
図11左は,図10のシミュレーション結果です.図10でAltキーを押しながら抵抗(RH)の上で左クリックすると,抵抗の電力が表示されます.図11左の電力の波形は,下側が丸まった三角波となっており,直観的に平均値がいくつかを把握することは難しいです.しかし,V(heater)*I(RH)をCtrlキーを押しながら左クリックすることで,図11右のように7.5Wとなっていることが確認できます.これは式9で計算した値と同じです.
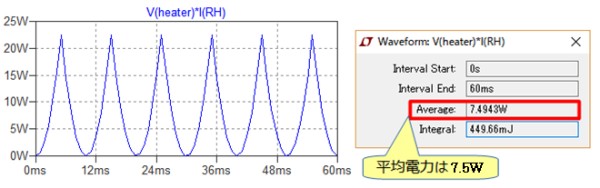
V(heater)*I(RH)をCtrlキーを押しながら左クリックし,平均電力7.5Wと確認できる.
図12左は,図10で抵抗に加わる電圧を表示したものです.また,V(heater)をCtrlキーを押しながら左クリックして表示されたウィンドウ(図12右)から,実効値が8.66VRMSであることが確認できます.これは式11で計算した値と同じです.
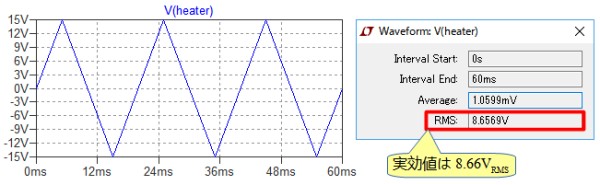
V(heater)をCtrlキーを押しながら左クリックし,実効値が8.66VRMSであることが確認できる.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice3_007.zip
●データ・ファイル内容
RMS_Q_A.asc:図3の回路
RMS_Q_B.asc:図6の回路
RMS_Q_C.asc:図9をシミュレーションする回路
RMS_Q_D.asc:図10の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










