コイルの理想と現実の特性を近づける

電子回路を組み立てるときに実際に使用するコイル(インダクタ)はシミュレータ上の理想コイルとは異なった特性を示します.そこで,図1のようにインピーダンス測定器を使用し,インダクタンスが47μHで,電源回路に使用されるコイルのインピーダンスの周波数特性を測定しました.
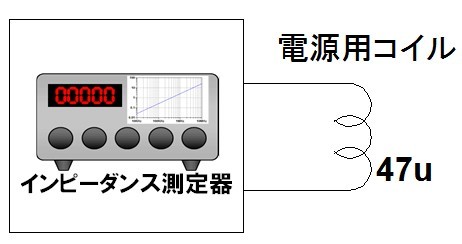
47μHの電源用コイルのインピーダンスの周波数特性を測定.
図2の(A)~(D)がその測定結果です.横軸が周波数で,縦軸がインピーダンスになっています.図2の(A)~(D)の中で,現実の電源用コイルのインピーダンス周波数特性を示すものはどれでしょうか?
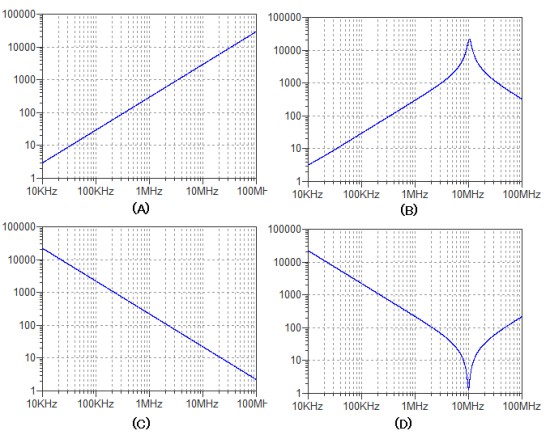
電源用コイルの特性として最も適切なものは?
理想コイルと現実のコイルは,異なった特性を示します.そこで,今回は,LTspice上で理想コイルを現実のコイルの特性に近づける方法を解説します.現実のコイルでは構造上,本来のインダクタンス成分以外に抵抗成分やキャパシタンス成分を含んでいいます.それを簡単な等価回路で表現すると,コンデンサと抵抗とコイルを並列に接続したものになります.その等価回路のインピーダンスの周波数特性がどのようになるかを考えれば,答えが分かります.
コンデンサと抵抗とインダクタの並列接続回路のインピーダンスは,特定周波数でそのインピーダンスが最大になり,山形の特性になります.そのような特性となっているのは(B)なので,正解は(B)ということになります.
●理想コイルと現実のコイル
理想コイルのインピーダンスは,周波数に比例して大きくなります.しかし,現実のコイルの特性はこれとは異なります.電源用コイルは,一般的にフェライトなどからできたコア材に,線材(銅線)を巻いて作られています.そのため,現実のコイルでは線材の抵抗やコア材の損失,線間の寄生容量などが発生します.その結果,現実のコイルは,特定の周波数以上になると,逆にインピーダンスが小さくなってしまいます.
この特性を表現するために,図3のような4素子等価回路が使われます.Lが本来のコイル(インダクタ)です.RSは主に線材の抵抗で,コイルの直流抵抗成分を表現し,RPはコイルの最大インピーダンスを表現するためのものです.CPは線材間の寄生容量です.L,RP,CPを並列接続したものにRSを直列に接続した等価回路もありますが,ほぼ同等の特性になります.
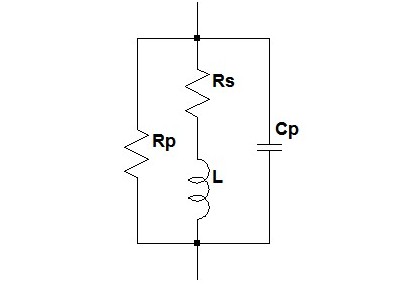
RSの位置が異なったものも使われる.
図3の回路のインピーダンスは式1で表されます.
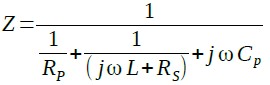 ・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・(1)
通常RSは数Ω以下と小さいため,最大インピーダンスを示す周波数では,ωL>> RSとなり,式1は,式2のように簡略化できます.
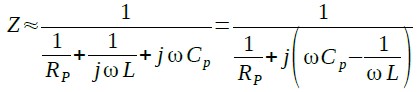 ・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・(2)
式2のインピーダンスの絶対値は式3のようになります.
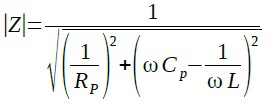 ・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3より,インピーダンスは「ωCP=1/ωL」のときに最大になり,そのときの値は,RPになることが分かります.「ωCP=1/ωL」となるωを求めると式4になります.
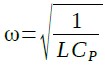 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
ここで「ω=2πf」なので,式4を変形して周波数(f)を求めると式5になります.
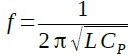 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
この周波数は並列共振周波数と呼ばれます.
●コイルのインピーダンスをシミュレーションする
図4は,コイルのインピーダンスをシミュレーションするための回路です.左が理想コイルで,右側が現実のコイルの等価回路です.
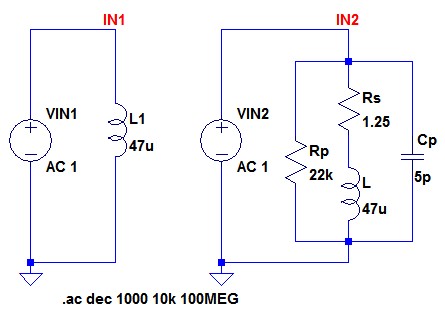
左が理想コイルで右側が現実のコイルの等価回路.
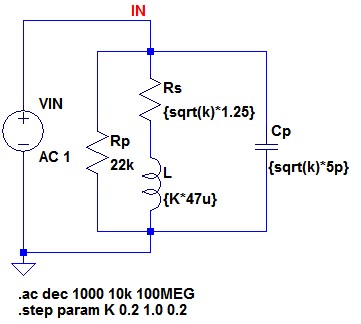
並列共振周波数は,式6から10.4MHzになります.そのときのインピーダンスは,RPと同じ22kΩになります.
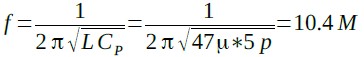 ・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・(6)
図5は,図4のシミュレーション結果です.V(IN1)/I(VIN1)のように,信号源の電圧を,その信号源の電流で割ることで,インピーダンスを表示させています.
図5を見ると分かるように理想コイルのインピーダンスが周波数に比例して大きくなっているのに対し,現実のコンデンサでは,約10MHzでインピーダンス最大となり,それ以上周波数が高くなるとインピーダンスが小さくなっていきます.このグラフは図2の(B)と同じものです.
現実のコイルは特定周波数以上になるとインピーダンスが低下する.
●コイルの値を変えてシミュレーションする
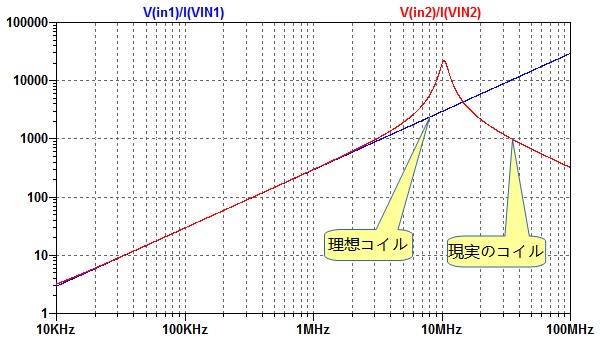
図6は,値が異なるコイルの特性を確認するため,インダクタンス値を変えてシミュレーションする回路です.コイルのインダクタンス値は,巻き数の二乗に比例します.直流抵抗(RS)は巻き数に比例し,寄生容量(CP)の値も巻き数に比例すると仮定すると,それぞれの値は,インダクタンス値の平方根に比例することになります.
そこで,コイルのインダクタンス値をKという変数を使って変化させ,直流抵抗(RS)と寄生容量(CP)の値は√Kという係数で変化させます.「.step param K 0.2 1.0 0.2」というコマンドでKを0.2から1.0まで0.2ステップで変化させます.
LとCPとRSの値をKという変数を使って変化させる.
図7は,図6のシミュレーション結果です.Lの値が小さいほど並列共振周波数は高くなり,コイルとして働く周波数が広くなります.
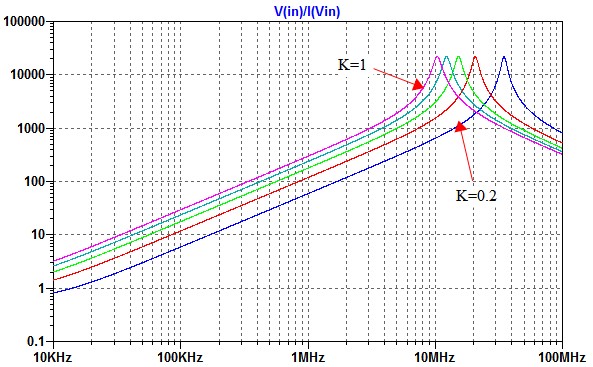
Lの値が小さいほど並列共振周波数は高くなる.
●等価回路をパラメータで表現する
より正確なシミュレーションを行うためには,単純なコイルではなく,図3のような等価回路を使用する必要があります.しかし,回路図に図3のような等価回路を配置すると,回路図が複雑になり,見づらくなってします.
LTspiceでは,図3のような等価回路を回路図に配置する代わりに,コイルのパラメータに等価回路の素子の値を入力することで,同等なシミュレーションを行うことができます.図8がコイルの4素子等価回路と,その等価回路をパラメータで表現したコイルの特性を比較するための回路です.
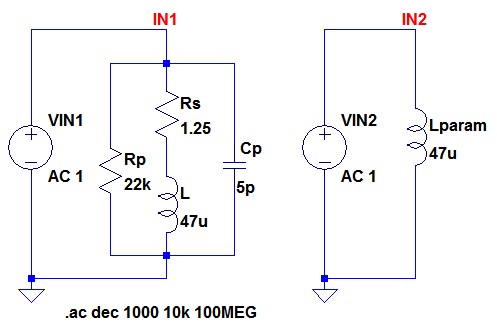
LTspiceは等価回路をパラメータで表現することができる.
図8の右側のLparamが等価回路をパラメータで表現したコイルです.コイルを右クリックして現れた図9のようなウィンドウの中でパラメータを指定します.
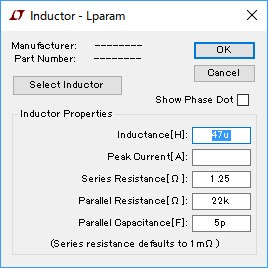
図8左の4素子等価回路と同じ値を入力してある.
図10は,図9のシミュレーション結果です.上が4素子等価回路の特性で,下がそれをパラメータで表現したコイルの特性ですが,両者の特性は全く同じになっています.
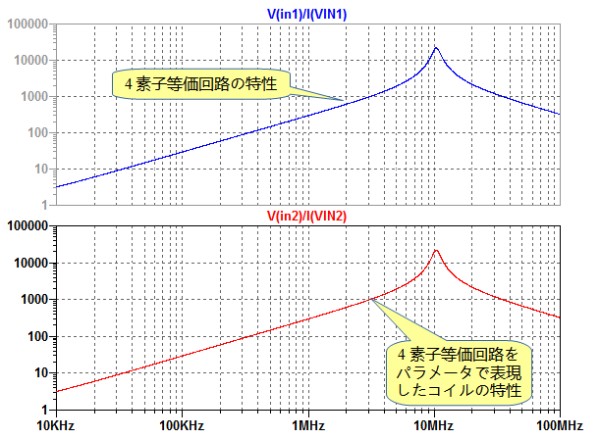
4素子等価回路の特性とそれをパラメータで表現したものは全く同じ特性となっている.
このように,LTspiceではコイルの等価回路をパラメータで表現することができるため,手軽により正確なシミュレーションを行うことができます.なお,「LTspice電源&アナログ回路入門 003」で紹介した,コンデンサの等価回路も,コンデンサのパラメータで表現することができます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice3_005.zip
●データ・ファイル内容
idealL_realL.asc:図4の回路
L_equ_cir_varL.asc:図6の回路
L_equ_cir_param.asc:図8の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










