回路の基本的な素子インダクタの電圧と電流

■問題

平賀　公久　Kimihisa Hiraga

　図1は，100μHのインダクタ（L₁）に周波数が50Hz，実効値が100mAの交流電流i(t)を印加した回路です．インダクタに流れる交流電流i(t)は，インダクタの電圧v(t)を基準にすると，位相は遅れます．

図1　インダクタL₁に交流電流i(t)を印加した回路
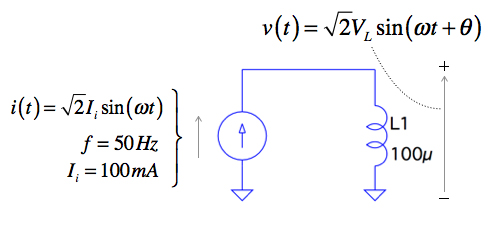
インダクタ：100μH，交流電流i(t)：50Hz，100mA．

　図2は，図1の交流電流i(t)とインダクタの電圧v(t)を図示しました．図1のL₁の電流i(t)と電圧v(t)との関係が正しいのは，図2の(a)～(d)のどれでしょうか？(a)と(b)は電圧の実効値が2.2mV，(c)と(d)は3.1mVです．また，(a)と(c)は，i(t)がv(t)より位相が90°遅れ，(b)と(d)は45°遅れています．

図2　図1の交流電流i(t)とインダクタの電圧v(t)の関係図
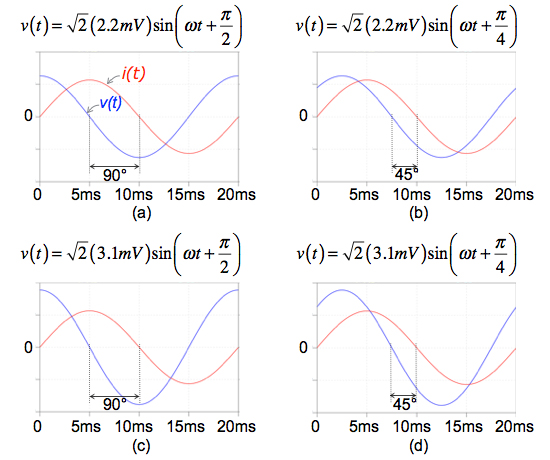
L₁の電流i(t)と電圧v(t)との関係が正しいのは？

■ヒント

　今回は，インダクタの電圧と電流の関係について解説します．インダクタに流れる電圧と電流は「v(t)=L₁*di(t)/dt」の関係があります．「i(t)=√2*I_iSIN(ωt)」より，v(t)の時間変化を求めると分かります．

　インダクタとは，直流は通し，周波数が高くなると通しづらい特性があります．インダクタの用途は，雑音を抑圧するLCフィルタや，降圧型DC-DCコンバータのチョークコイルなどに使われます．インダクタはコイルのことであり，誘導性（Inductive）であることから，その名称がついています．

■解答

(c)

電圧の実効値が3.1mV，i(t)はv(t)に比べ位相が90°(π/2)遅れる

　インダクタの電圧は，インダクタンス(L₁)，電流i(t)，時間(t)で表すと式1の関係があります．

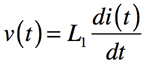・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

　また，電流は式2であり「ω=2πf」です.

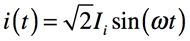・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

　図1より，L₁のインダクタンスは100μH，電流の振幅は√2*100mA，周波数(f)は50Hzより「ω=100π」です．式2を式1へ代入し整理すると式3となります．

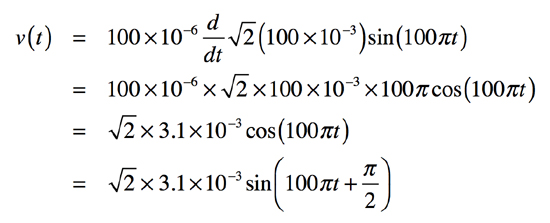・・・・・(3)

　式3より，電圧の実効値は3.1mVで，周波数(f)は電流と同じ50Hzです．また，式2の電流i(t)を基準とすれば，式3の電圧v(t)は位相が90°進みます．言い換えれば，電圧v(t)を基準にすると，電流i(t)は90°遅れます．以上より，解答は(c)となります．

■解説

●インダクタは導線を巻いたもの
　図3は，導線でループを作ったインダクタのモデルを使い，図1を書き直しました．インダクタへの電流は矢印の向きに流れ，ループの長さをl，ループの面積をA，電流により生じる磁界をB(t)，透磁率をμとして表しています．
　インダクタに交流電流を流すと右ねじの法則で磁界が生まれ，磁束も変化するため，インダクタには自己誘導による起電力が生じます．この起電力は，インダクタに流れる電流とは反対になる電流を流そうとするため，高周波になるほどコイルに流れる電流を阻止する働きとなります．図3の巻数は，1つですが，実際のインダクタは複数の巻数で作られています．透磁率を大きくするには，巻いた内側の空洞にコアを入れます．インダクタの単位はH（ヘンリー）を使い，1秒間に電流が1A変化したとき，電圧が1V変化すれば1Hとなります.

図3　図1を導線でループを作ったインダクタのモデルを使い示した図
インダクタに交流電流を流すと右ねじの法則で磁界が生まれ，磁束も変化するため，インダクタには自己誘導による起電力が生じる．

●インダクタの電圧と電流の比例関係を導く
　ここでは，図3用いてインダクタの電圧と電流の関係を導き，その性質を理解します．図3のループの長さをl，ループ内の面積をA，透磁率をμとすれば，磁界B(t)は式4となります.

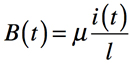・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　このときの磁束Φと電流の関係は，式5となります.

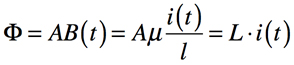・・・・・・・・・・・・・・・・・・・・・・(5)

　ここで，Lは自己インダクタンスであり，式6となります.

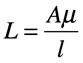・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　インダクタの電圧は，磁束を時間で微分した関係があり式７となります．式７はインダクタの電圧と電流の比例関係を示しています．

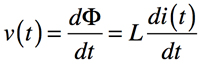・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　以上より，解答の計算で使った最初の式1が導出されました．解答では式7を使い，電流の実効値と位相を調べています.実際のインダクタは，導線を複数回巻いて作られています．この場合の自己インダクタンスは式8となります．式8のkは長岡係数，またnは巻数です．長岡係数とは，ソレノイドコイル（らせん状のコイル）のインダクタンスを求めるときに使う係数です.

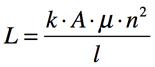・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)

●インダクタの電圧をLTspiceで確かめる
　図4は，図1をシミュレーションする回路で，インダクタの電圧V_Lを調べます．また，インダクタに流れる電流は赤の矢印方向をプロットします．

図4　図1をシミュレーションする回路
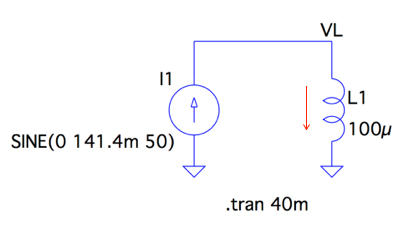
インダクタの電圧V_Lを調べる．

　図5は，図4のシミュレーション結果です．まず，電圧波形の振幅をカーソルで調べると4.4mVです．これは√2×3.1mVと同じであり，解答の実効値と同じであることがわかります．実効値はプロットからも求めることができ，図5のv(vl)のラベルの上にカーソルを置き，Ctrl+左クリックで現れる図6の小さなウィンドウから，3.1mVであることがわかります.

図5　図4のシミュレーション結果
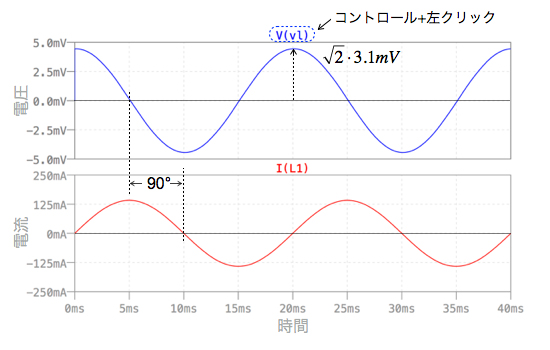
電圧波形の振幅をカーソルで調べると4.4mV．

図6　電圧波形の実効値を表示
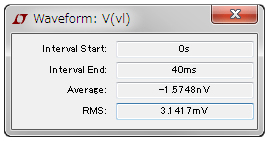
プロットしている波形のラベルの上で，コントロールキーを押しながら左クリック．

　次に電圧が0Vと交差する時間と同じように，電流が0Aと交差する時間に着目します．解答の計算で得たように，インダクタの電圧を基準とすると，インダクタに流れる電流は90°遅れます．図5では電圧波形は5msで0Vになります．電流はそれより後の時間の10msで0Aになり，1/4周期遅れていることがわかります．1周期は360°（弧度法で2π）ですので，1/4周期は90°（弧度法でπ/2）となり，解答の計算と同じになります.

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice3_004.zip

●データ・ファイル内容
L_Voltage.asc：図4の回路