一次移相回路の最大の位相シフトは何度?

図1は,同じ抵抗値の三つの抵抗R,コンデンサC,OPアンプを使った一次移相回路です.移相回路は,オール・パス・フィルタとも呼ばれ,入力周波数に関係なくゲインは一定で,位相シフトした波形を出力します.図1の一次移相回路は,直流を入力したときは,入力と出力が同じ波形(位相0°)であり,周波数が高くなるにつれ,位相がシフトします.図1の一次移相回路において,最大の位相シフトは(a)~(d)のどれでしょうか? ここでOPアンプは理想とします.
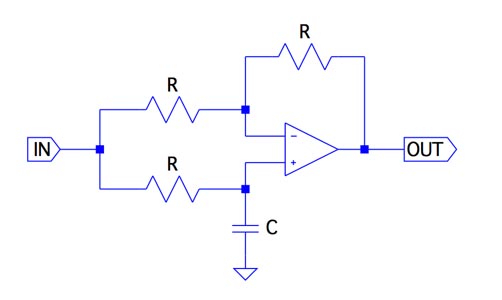
入力周波数に関係なくゲインは一定で,位相シフトした波形を出力する.
周波数が高くなると,OPアンプの非反転端子につながるコンデンサCのインピーダンスは小さくなります.また,無限大周波数のとき,Cの両端が同じ値でショートとなり,GND状態と見なされ,Cの値はゼロと考えることができます.図1の回路をCの値がゼロのに書き換え,出力の位相シフトを考えると分かります.
図1の位相シフトの範囲は,定性的な回路の動作を考えることで,簡単に求めることができます.一次移相回路は,入力の周波数が高くなると出力は位相シフトします.位相シフトの範囲を決める条件は,二つあります.一つ目は,最小の位相シフトで,初期値の直流を入力した場合,入力と出力が同じ波形となり位相が0°になります.二つ目は,最大の位相シフトで,無限大周波数の場合です.
また,OPアンプを理想とすれば,周波数の変化で回路の状態が変わるのは,コンデンサのインピーダンスです.コンデンサのインピーダンスは,直流のとき,無限大であり,回路がオープンな状態となります.無限大周波数のとき,インピーダンスはゼロであり,ショートの状態となります.
この二つの状態を図2に示します.図2(a)(b)との状態について位相シフトを考えます.図2(a)のときは,OPアンプの二つの入力端子は,バーチャル・ショートとなり,ボルテージ・フォロワ回路の動作となります.よって,入力と出力は同じ波形になり,位相遅れはありません.図2(b)は無限大周波数のときであり,OPアンプの非反転端子はGNDとなります.非反転端子がGNDの状態は,ゲインが-1の反転増幅器として働き,入力と出力の波形は反転することから,位相シフトは-180°です.以上より答えは(d)-180°となります.
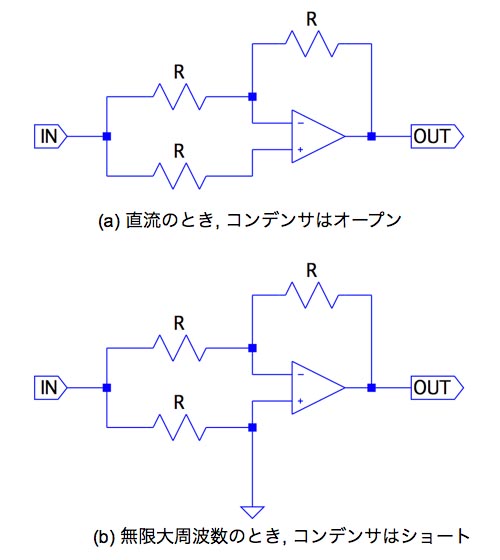
(a)は直流のとき,コンデンサはオープン.
(b)は無限大周波数のとき,コンデンサはショート.
●一次移相回路の定量的な回路解析
一次移相回路の伝達関数は重ね合わせの理を使うと簡単に求まります.図3は,図1の回路の入力の信号源を二つに分けました.これを用いて,vi1が信号源でvi2をショートしたときのvo1を求め,次にvi2が信号源でvi1をショートしたときのvo2を求めます.重ね合わせの理より「vo(s)=vo1(s)+vo2(s)」となります.ここでは,求めた伝達関数からゲインと位相を調べます.
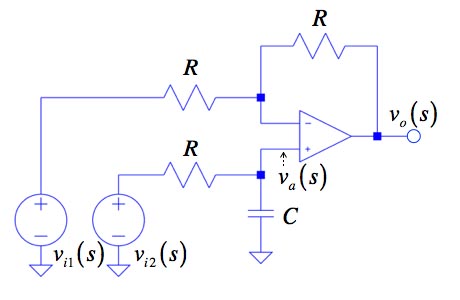
入力を二つの電圧源で示した.
vi1が信号源でvi2をショートしたとき
「ゲイン=-1」の反転増幅器となりますので,このときの伝達関数は式1となります.
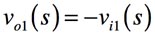 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
vi2が信号源でvi1をショートしたとき
OPアンプの非反転端子の電圧vaが入力となる非反転増幅器となります.vaは,vi2をRとCのインピーダンスで分圧した値なので,式2となります.
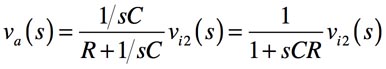 ・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・(2)
したがってvo2は,式3となります.
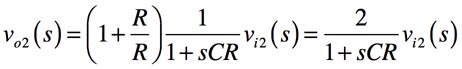 ・・・・・・・・・・・(3)
・・・・・・・・・・・(3)
「vi1(s)=vi2(s)=vi(s)」であること,また重ね合わせの理より,式1と式3を使い出力電圧を求めると式4となります.
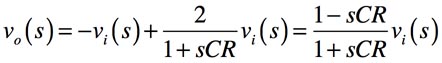 ・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・(4)
以上より,図3の伝達関数は「s=jω」と置換して,式5となります.
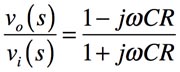 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
次に,式5を使って一次移相回路のゲインと位相を調べます.ゲインは,式5の絶対値ですので,式6となります.式6より,一次移相回路のゲインは,周波数に関係なく「ゲイン=1」となります.
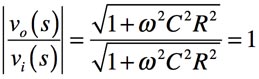 ・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・(6)
位相は,式5を書き換えて式7とします.
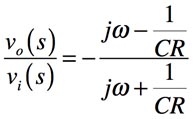 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7の分子の位相をθ1,分母の位相をθ2とすれば,一次移相回路の位相は「θd=θ1-θ2」であり,式8となります.式8より,位相は周波数に応じて位相シフトします.
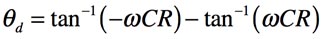 ・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・(8)
ただし,ω=2πf
●周波数の変化による位相シフトを計算で調べる
前述の式8を使い「ω=0(直流)」,「ω=1/CR(CとRのコーナー周波数)」,「ω=∞(無限大周波数)」の3条件について,具体的な位相シフトを求めます.
条件1「ω=0」
条件1は,直流の状態で,図2(a)に相当します.位相シフトは式9となり,直流での位相シフトはありません.
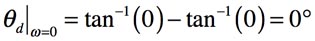 ・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・(9)
条件2「ω=1/CR」
条件2は,CとRのコーナー周波数です.位相シフトは式10となり,出力は入力より-90°の遅れた信号になります.
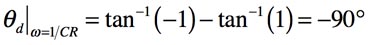 ・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・(10)
条件3「ω=∞」
条件3は,無限大周波数のときで,図2(b)に相当し,解答の位相シフトを計算で求めます.位相シフトは式11となり,出力は入力より-180°の遅れた信号になります.
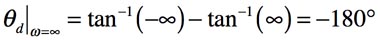 ・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・(11)
●一次移相回路をLTspiceで確かめる
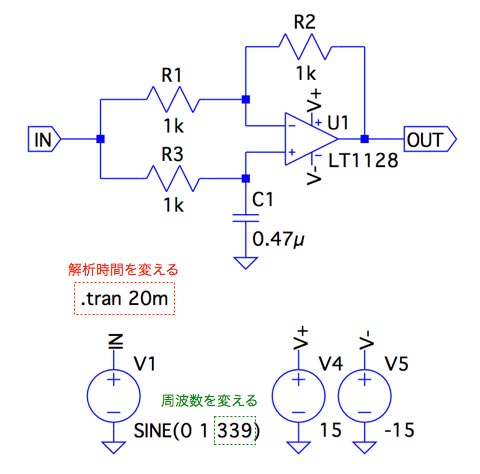
図4は,一次移相回路の周波数特性を調べる回路です.「R1=R2=R3=1kΩ」,「C1=0.47μF」,OPアンプはLT1128を使用しました.条件2の周波数は「f=1/2πf(1kΩ)(0.47μF)=339Hz」です.
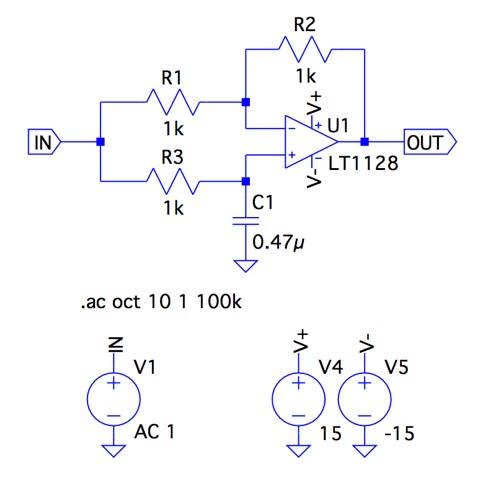
周波数特性はゲインと位相を調べる.
図5は,図4のシミュレーション結果です.式6で求めたとおり,ゲインは周波数に依存せず,0dB(1倍)です.また,位相シフトは式9,式10,式11で求めた3条件のとおりになっています.
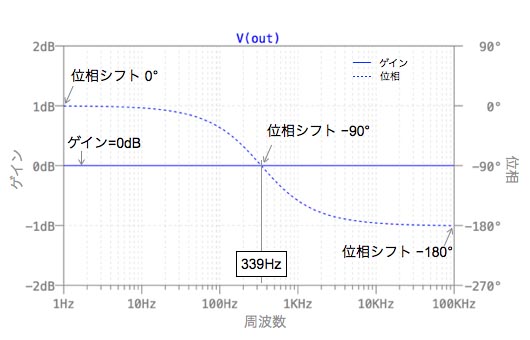
ゲインは周波数に依存せず,0dB(1倍)です.
●過渡解析で波形の遅れを確かめる
図6は,一次移相回路の過渡解析をおこなうシミュレーション回路です.条件1,条件2,条件3で求めた式9,式10,式11の値を別々にシミュレーションするため,入力の周波数と解析時間は,図6の回路図を編集します.
具体的には,次のような値としました.
条件1:周波数1Hz,過渡解析のストップ時間 6s (1Hzの低周波を直流に近い値として)
条件2:周波数339Hz,過渡解析のストップ時間 20ms
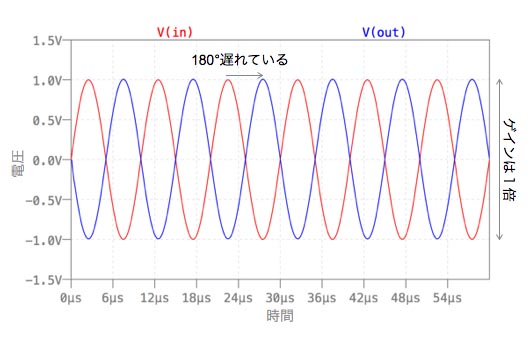
条件3:周波数100kHz,過渡解析のストップ時間 60μs (条件2よりも十分高い周波数として)
条件1,条件2,条件3で求めた値を別々にシミュレーションする.
図7は,1Hzの低周波のときです.入力と出力は重なっており,ゲインは1倍です.また,位相シフトは0°となります.
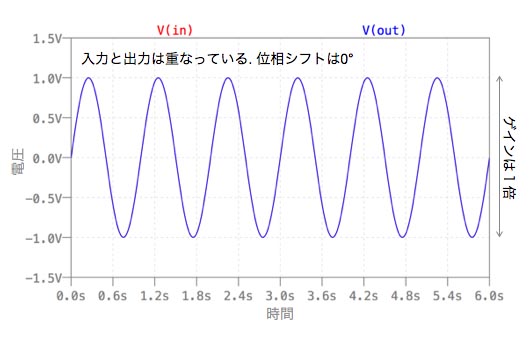
図8は,339Hzのときです.ゲインは1倍で,時間軸での遅れは,位相シフト-90°分です.
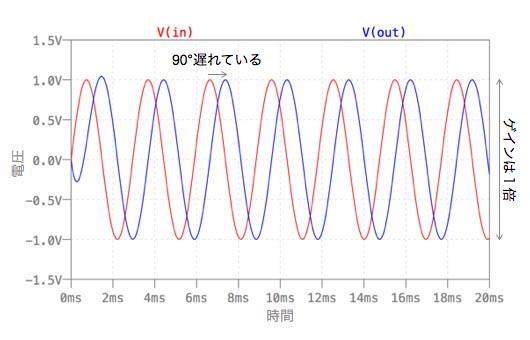
図9は,100kHzのときです.ゲインは1倍で,時間軸での遅れは,位相シフト-180°分です.
以上のシミュレーション結果からも分かるように,一次移相回路はゲインを変えずに位相シフトする回路となります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_048.zip
●データ・ファイル内容
Phase_Shifter_ac.asc:図4の回路
Phase_Shifter_tran.asc:図6の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










