全波整流になる抵抗の組み合わせはどれ?

図1はOPアンプ,ダイオード,抵抗を使った全波整流回路です.入力電圧(VIN)が正と負(VIN>0,VIN<0)の状態で回路が切り替わります.また,「R1=R3=R4=1kΩ」としたとき,R2,R5を適切に調整すると,全波整流された出力がOUT端子に現れる回路です.V1の電圧源からOUT端子までのゲインが1倍で,全波整流になる抵抗(R2,R5)の組み合わせは,(a)~(d)のうちどれでしょうか?
ここで計算を簡単にするため,OPアンプ(U1,U2)は理想とします.
(c)R2=1kΩ,R5=2kΩ,(d)R2=2kΩ,R5=2kΩ
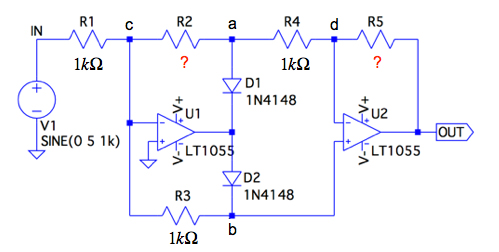
まず,この問題では「VIN>0」の半波のときを考えます.図1のダイオード(D1,D2)は,入力電圧が正(VIN>0)のとき,OPアンプU1の出力電圧の極性より,D1とD2のどちらかのダイオードがOFFになります.ゲインの計算は,OFFになるダイオードを回路から取り外し,OPアンプU1を使ったゲイン(G1)を持つ増幅回路と,OPアンプU2を使ったゲイン(G2)をもつ増幅回路が「G1*G2=1」となる抵抗の組み合わせを考えると分かります.
入力電圧が正(VIN>0)の半波のとき,OPアンプU1と抵抗(R1,R2),ダイオードD1で構成した反転増幅器の出力は,GNDより電圧が下がります.D2のカソードはOPアンプU1のバーチャル・グラウンドの電圧ですので,ダイオードD2が逆バイアスとなってOFFします.
次にD2を回路から取り外した状態で考えます.OPアンプU1と抵抗(R1,R2)の反転増幅器の出力はa点であり,そのゲインは 「G1=-(R2/R1)」となります. 次にR3の左側となるc点の電圧は,OPアンプU1のバーチャル・グラウンドであり,OPアンプU2と抵抗(R4,R5)は反転増幅器として働き,そのゲインは,「G2=-(R5/R4)」となります.
以上より,入力から出力までのゲインは「G1*G2=(R2R5)/(R1R4)」となります.「G1*G2=1」とするには「R1=1kΩ,R4=1kΩ」ですので,(a)の「R2=1kΩ,R5=1kΩ」となり,図1のR1~R5は同じ抵抗値となります.
●ダイオード・ブリッジを使った全波整流回路
図2は,ダイオード・ブリッジ(D1~D4)と負荷抵抗(RL)を使った全波整流回路です.入力信号は振幅が5V,周波数が1kHzの信号を入力しました.ダイオード・ブリッジを用いた全波整流回路は,回路も簡単なことから広く使われています.
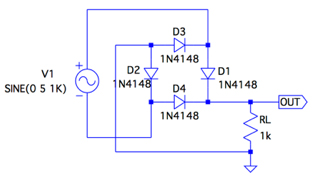
図3は,図2の入力電圧の極性が変わったときの電流の流れる経路を示しました.図3(a)が交流の最初の半波,図3(b)が図3(a)と極性が逆になる次の半波の状態です.入力信号の極性が変わることにより,ダイオードがスイッチとして働き,流れる電流の経路を変え,負荷抵抗(RL)には同じ電流の向きで流れます.この電流経路の切り替えにより,出力電圧は全波整流となります.
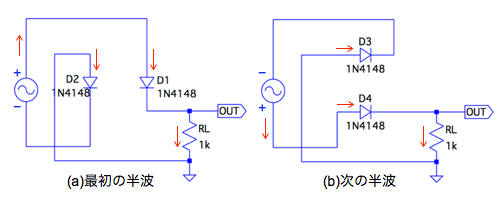
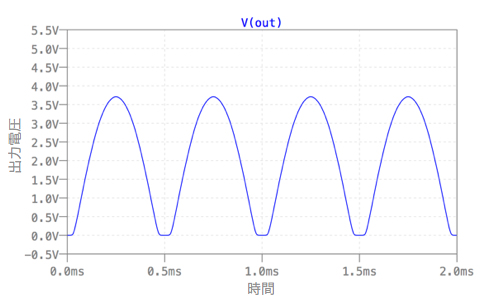
図4は,図2をシミュレーションした結果です.入力信号は,振幅が5Vの正弦波ですので,全波整流した出力の最大値は5Vを期待しますが,ダイオード・ブリッジを使った全波整流回路は,図4の波形からも明らかなように,ダイオードの順方向電圧があり,出力電圧はその分だけ低くなります.これを改善するのが図1に示す全波整流回路となります.
●同じ抵抗値でつくる全波整流回路
図1は,同じ抵抗値で構成できる全波整流回路です.入力電圧が正と負(VIN>0,VIN<0)の状態で回路が切り替わるため,入力電圧が正と負の条件について解説します.
「VIN>0」の場合
図5は「VIN>0」の状態を示し,ダイオードD2がOFFになるので,回路からD2を取り除いた等価回路図です.
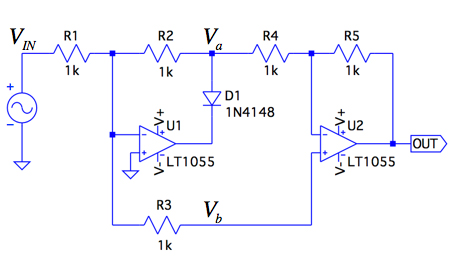
D2はOFFのため,回路から取り除いた.
解答で計算した通り「VIN>0」のときは,OPアンプU1と抵抗(R1,R2)で構成した反転増幅回路とOPアンプU2と抵抗(R4,R5)で構成した反転増幅回路の縦続接続となります.図5の記号を使い縦続接続した二つの増幅回路の入力と出力の関係を調べます.
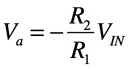 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
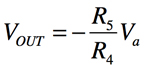 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式1,式2より,式3がVIN>0のときの入力と出力の関係となります.
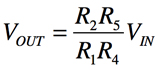 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
「VIN<0」の場合
図6は「VIN<0」の状態を示し,ダイオードD1がOFFになるので,回路からD1を取り除いた等価回路図です.図6を使い「VIN<0」のときの入力と出力の関係を調べます.
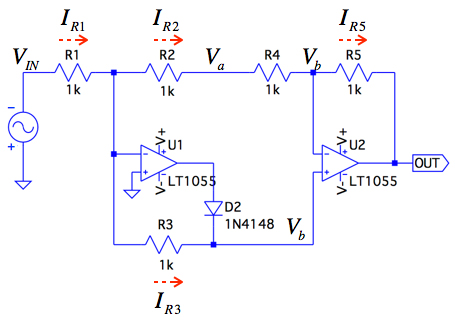
D1はOFFのため,回路からD1を取り除いた.
OPアンプU1の反転端子は,バーチャル・グラウンドであり0Vです.OPアンプU2の反転端子は,バーチャル・ショートにより,非反転端子と同じVbとなります.そこで,抵抗(R1,R2,R3,R4)に流れる電流(IR1,IR2,IR3,IR4)は,図6より式4となります.
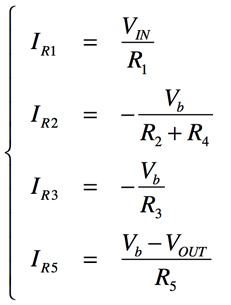 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
R1の電流は,R2とR3に分流するため「IR1=IR2+IR3」であり,式5となります.
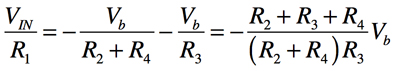 ・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・(5)
次にR2に流れる電流はR5となります.したがって「IR2=IR5」より式6となります.
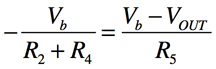 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式6を整理して,VbとVOUTの関係を調べると式7となります.
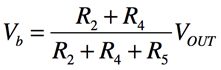 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式5へ式7を代入し整理すると式8になります.
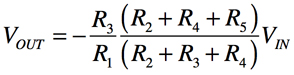 ・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・(8)
式8は「VIN<0」のときの入力と出力の関係を表しています.
「VIN>0」のときの入力と出力の関係は式3で,「VIN<0」のときの入力と出力の関係は式8です.なので,「R1=R2=R3=R4=R5」の場合,「VIN>0」のとき「VOUT=VIN」で,「VIN<0」のとき「VOUT=-VIN」となります.よって「VOUT=|VIN|」の全波整流回路となります.
●全波整流回路の特性をLTspiceで確かめる
図7は,図1をシミュレーションする回路です.
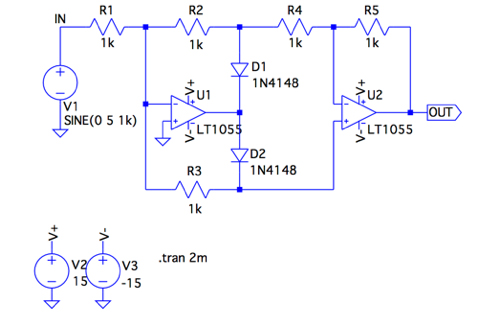
図8は,図7のシミュレーション結果です.入力電圧を全波整流した出力が得られています.図4に示したダイオード・ブリッジを用いた全波整流出力のように,ダイオードの順方向電圧に制限を受けません.
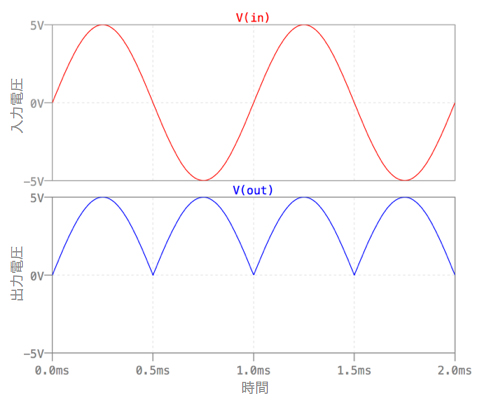
入力波形,出力波形を示した.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_042.zip
●データ・ファイル内容
Full_Wave_Rectifier.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










