2相発振回路の周波数の式は?

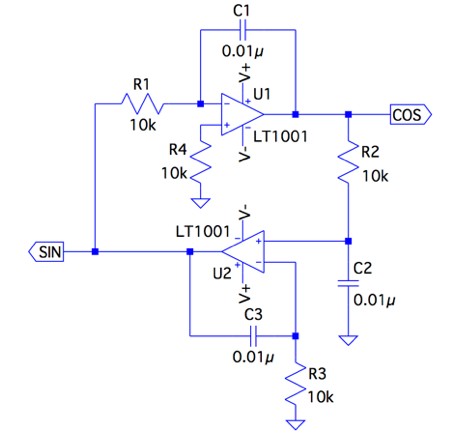
図1は,OPアンプを使った2相発振回路(Quadrature Oscillator)です. 回路は,二つのOPアンプ(LT1001)と三つのコンデンサ(C1=C2=C3=0.01μF),四つの抵抗(R1=R2=R3=R4=10kΩ)で構成されています.2相発振回路の出力の一つは正弦波であり,もう一つは位相が90°違う出力波形が得られます.図1では,「SIN」および「COS」が出力となります.図1の2相発振回路で,OPアンプを理想としたとき,発振周波数の式は(a)~(d)のうちどれでしょうか?
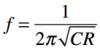 , (b)
, (b)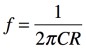 , (c)
, (c)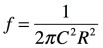 , (d)
, (d)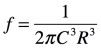
図1のR1,R4,C1,U1は,「SIN」が入力,「COS」が出力のOPアンプを使った反転積分回路です.その伝達関数は「G1=-1/sC1R1」となります.また,R2,R3,C2,C3,U2は,「COS」が入力,「SIN」が出力のOPアンプを使った差動積分回路です.その伝達関数は「G2=(1+sC3R3)/(1+sC2R2)sC3R3」です.ここで「s=jω」なので,ループ・ゲインは,これら二つの伝達関数の積であり,発振条件の「ループ・ゲインは1」より,発振周波数が求まります.2相発振回路は直角位相発振器(Quadrature Oscillator)とも呼ばれます.
図1の2相発振回路を二つのブロックに分けて考えます.第1のブロックは,「SIN」が入力「COS」が出力のR1,R4,C1,U1からなる反転積分回路です.第2のブロックは,「COS」が入力,「SIN」が出力のR2,R3,C2,C3,U2からなる差動積分回路です.第1の反転積分回路の位相は270°遅れで,第2の差動積分回路の位相は90°遅れるため,図1は,全体で360°遅れる正帰還ループを構成しています.発振周波数の計算は,第1の反転積分回路と第2の差動積分回路の伝達特性を求め,これら二つの積であるループ・ゲインを計算し,発振条件となる「ループ・ゲインが1」より求めます. ここで計算を簡単にするため,OPアンプは理想とします.
図1の第1のブロックである反転積分回路の伝達関数は式1となります.
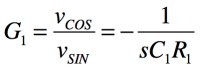 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
同様に,第2のブロックである差動積分回路の伝達関数は式2となります.
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
同様に,第2のブロックである差動積分回路の伝達関数は式2となります.
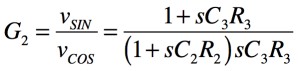 ・・・・・・・・・・・・・・・・・・・・・・(2)
図1の2相発振回路のループ・ゲインは,式1と式2の積です.また,コンデンサは「C1=C2=C3」ですのでCとし,抵抗は「R1=R2=R3」ですのでRとすると,式3となります.
・・・・・・・・・・・・・・・・・・・・・・(2)
図1の2相発振回路のループ・ゲインは,式1と式2の積です.また,コンデンサは「C1=C2=C3」ですのでCとし,抵抗は「R1=R2=R3」ですのでRとすると,式3となります.
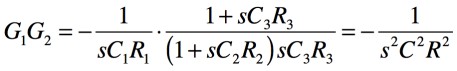 ・・・・・・・・・・・・(3)
式3で,「s=jω」とし,発振条件はループ・ゲインが1ですので,式4となります.
・・・・・・・・・・・・(3)
式3で,「s=jω」とし,発振条件はループ・ゲインが1ですので,式4となります.
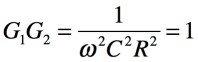 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4で,ループ・ゲインを1にするには「ω=1/CR」です.このときωが発振周波数であり「ω=2πf」なので,解答は(b)の式となります.具体的な発振周波数は,図1の回路定数「C=0.01μF」,「R=10kΩ」および「ω=2πf」より,式5となります.
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4で,ループ・ゲインを1にするには「ω=1/CR」です.このときωが発振周波数であり「ω=2πf」なので,解答は(b)の式となります.具体的な発振周波数は,図1の回路定数「C=0.01μF」,「R=10kΩ」および「ω=2πf」より,式5となります.
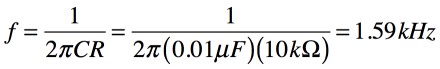 ・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・(5)
●2相発振回路は反転積分回路と差動積分回路でできている 図2は,2相発振回路のブロック図です.2相発振器は反転積分回路と差動積分回路で構成します.反転積分回路の出力は差動積分回路の入力へ,差動積分回路の出力は反転積分回路の入力となりループを作ります.ここで,二つの回路の位相に着目します.反転積分回路は出力が反転するため180°の位相差があり,さらに積分回路の位相遅れが90°ありますので,270°の遅れとなります.次に差動積分回路は90°の遅れが生じ,ループ全体の位相は360°遅れ(位相差は0°と同じ),正帰還ループとなります.この状態でループ・ゲインが1となれば,正弦波で発振します.COS出力とSIN出力は90°の位相差があり,よって,正弦波と余弦波の二つの出力を得ることができます.
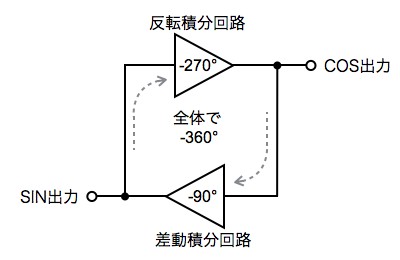
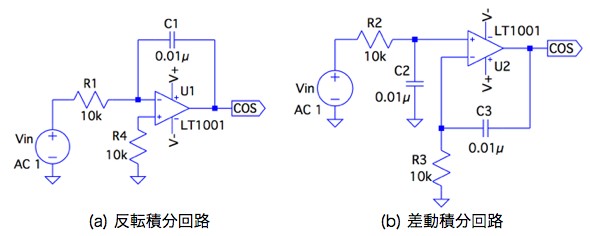
図3(a)(b)は,図1の2相発振器を構成する反転積分回路と差動積分回路を分離した回路です.図3(a)が反転積分回路で,図3(b)が差動積分回路です.
この二つの回路の周波数特性を調べると,図4が反転積分回路のゲインと位相の周波数特性で,図5が差動積分回路のゲインと位相の周波数特性となります.二つのグラフには,解答で計算した発振周波数 1.59kHzに線を引きました.
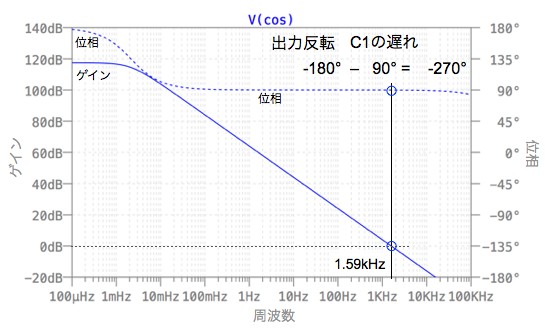
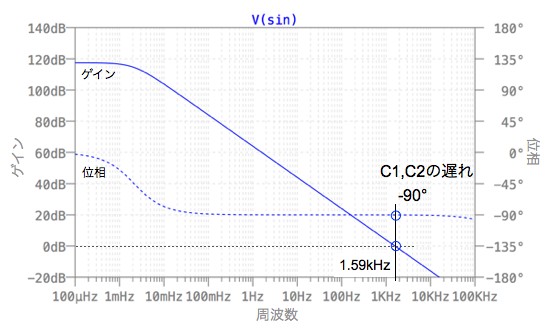
図4の反転積分回路では,直流の状態から出力の極性が反転するので,低周波の位相は180°から始まり,発振周波数では位相はさらに90°遅れ,270°の遅れになっていることが分かります.図5の差動積分回路の位相は,低周波では0°から始まり,発振周波数では90°遅れます. これより,図1のように,この二つの回路を組み合わせたループの位相は,-360°であり正帰還となります.次に図4,図5の1.59kHzのゲインを調べると両方とも0dB(1倍)であり,二つの回路を接続したループ・ゲインは0dB(1倍)となることから,1.59kHzで発振することになります.
●2相発振回路の発振条件を算出する
図1の2相発振器は,OPアンプを理想として考えると,発振する条件に「C2R2=C3R3」があります.ここでは,2相発振回路のループ・ゲインを示す式3を用いて,発振条件を算出します.
式3の左辺と右辺第1項を使い,「s=jω」とすると,式6となります.
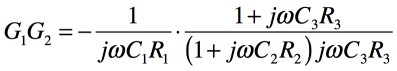 ・・・・・・・・・・・・・・・・(6)
さらに式を整理し,発振条件のループ・ゲインは1ですので,式7となります.
・・・・・・・・・・・・・・・・(6)
さらに式を整理し,発振条件のループ・ゲインは1ですので,式7となります.
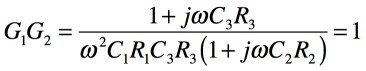 ・・・・・・・・・・・・・・・・・・(7)
式7のループ・ゲインが1になるには,式8と式9の関係が必要となります.
・・・・・・・・・・・・・・・・・・(7)
式7のループ・ゲインが1になるには,式8と式9の関係が必要となります.
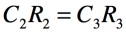 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
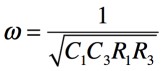 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
以上より,2相発振器は発振する条件に「C2R2=C3R3」があります.式8と式9の条件が揃ったときの発振周波数は,式10となります.
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
以上より,2相発振器は発振する条件に「C2R2=C3R3」があります.式8と式9の条件が揃ったときの発振周波数は,式10となります.
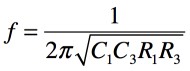 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
実際のOPアンプは,有限のオープン・ループ・ゲインですので,R2をわずかに大きくすると,発振の成長も早くなり,安定して発振します.
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
実際のOPアンプは,有限のオープン・ループ・ゲインですので,R2をわずかに大きくすると,発振の成長も早くなり,安定して発振します.
●2相発振回路の出力電圧をLTspiceで確かめる 図6は,図1の2相発振回路をシミュレーションする回路.
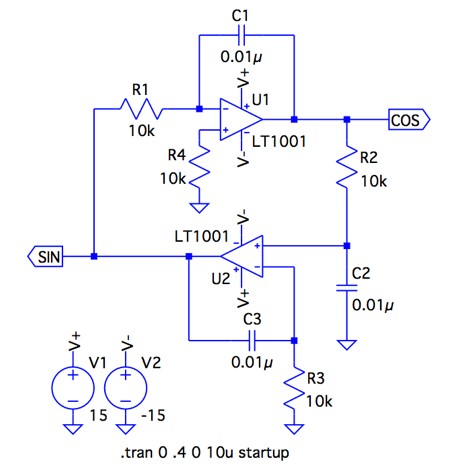
図7は,図6のシミュレーション結果です.発振周波数1.59kHzのSIN出力とCOS出力が得られています.図6の2相発振器の欠点は,発振振幅の制限回路がないため,OPアンプの最大出力電圧で飽和します.このため,正負の最大出力電圧付近で波形がひずんでいます.
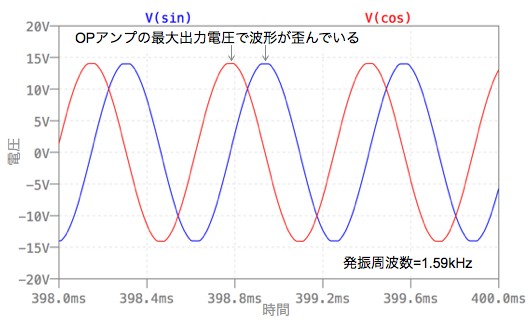
●ダイオード・リミッタ付き2相発振回路
図6のOPアンプの最大出力電圧付近で波形がひずまない対策として,OPアンプの出力が飽和しないように,出力振幅を制限するリミッタ回路を加えれば,2相発振器の出力波形はひずみが少なくなります.リミッタ回路により非線形になっても,SIN出力とCOS出力は反転積分回路と差動積分回路のLPF (Low Pass Filter)の作用により,高調波ひずみの周波数成分は抑圧されるからです.
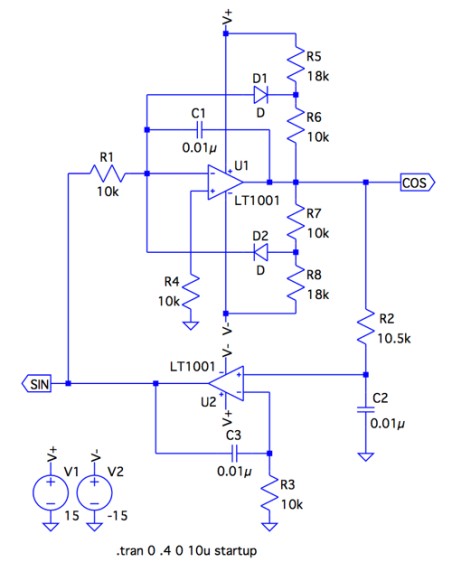
図8は,図1の2相発振回路に,R5,R6,R7,R8とD1,D2からなるリミッタ回路を付け加えた回路です.このリミッタ回路は,COS出力の発振振幅が大きくなるとD2が導通します.反対に発振振幅が小さくなるとD1が導通して発振振幅を制限します.
ダイオードの順方向電圧をVD,回路の電源電圧V+とV-の絶対値をVSとすれば,リミッタ回路のダイオードが導通した直後のCOS出力の電圧は,D2が導通したときは式11です.
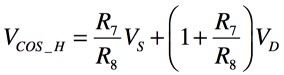 ・・・・・・・・・・・・・・・・・・・・・・(11)
D1が導通したときは式12となります.
・・・・・・・・・・・・・・・・・・・・・・(11)
D1が導通したときは式12となります.
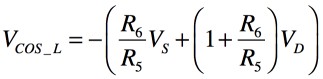 ・・・・・・・・・・・・・・・・・・・・(12)
ここで「VD=0.6V」,「VS=15V」とし,図8の抵抗値を用いて計算すると,「VCOS_H=9.26V」,「VCOS_L=-9.26V」となります.このリミッタ回路は,発振回路の振幅の調整回路としてよく用いられます.また,図8のR2は,発振が安定するように,僅かに抵抗を大きくして10.5kΩとしました.
・・・・・・・・・・・・・・・・・・・・(12)
ここで「VD=0.6V」,「VS=15V」とし,図8の抵抗値を用いて計算すると,「VCOS_H=9.26V」,「VCOS_L=-9.26V」となります.このリミッタ回路は,発振回路の振幅の調整回路としてよく用いられます.また,図8のR2は,発振が安定するように,僅かに抵抗を大きくして10.5kΩとしました.
●ダイオード・リミッタ付き2相発振回路の出力電圧を確かめる
図9は,図8のダイオード・リミッタ付き2相発振回路をシミュレーションした結果です.SIN出力,COS出力とも図7のようなひずみはありません.
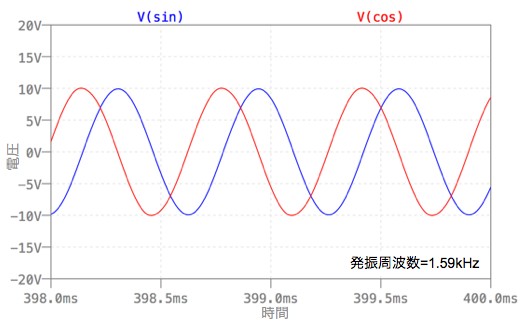
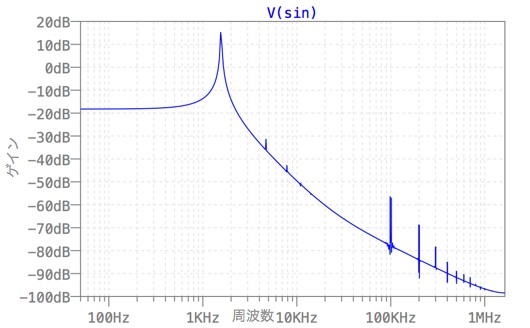
図10は,図9のSIN出力をフーリエ変換した結果です.高調波が少なく,ひずみが少ないことが分かります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_038.zip
●データ・ファイル内容
Quadrature.asc:図6の回路
Quadrature_with_Limitter.asc:図8の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










