ウィーン・ブリッジ発振回路が適切に発振する抵抗値はいくら?

図1は,OPアンプ(LT1001)を使ったウィーン・ブリッジ発振回路(Wein Bridge Oscillator)です. 回路は,OPアンプ,二つのコンデンサ(C1= C2=0.01μF),四つの抵抗(R1=R2=R3=10kΩとR4)で構成しました.R4は,非反転増幅器のゲインを決める抵抗で,R4を適切に調整すると,正弦波の発振出力となります.正弦波の発振出力となるR4の値は,次の(a)~(d)のうちどれでしょうか.なお,計算を簡単にするため,OPアンプは理想とします.
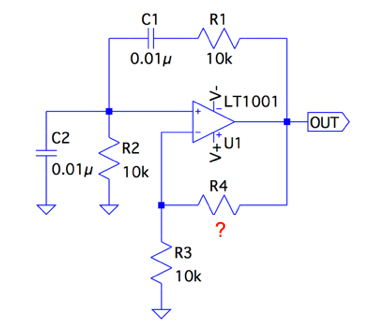
ウィーン・ブリッジ発振回路は,OPアンプの出力から非反転端子へR1,C1,R2,C2を介して正帰還しています.この帰還率β(jω)の周波数特性は,R1とC1の直列回路とR2とC2の並列回路からなるバンド・パス・フィルタ(BPF)であり,中心周波数の位相シフトは0°です.その信号がOPアンプとR3,R4で構成する非反転増幅器の入力となり「|G(jω)|=1+R4/R3」のゲインで増幅した信号は,再び非反転増幅器の入力に戻り,正帰還ループとなります.帰還率β(jω)の中心周波数のゲインは1より減衰しますので「|G(jω)β(jω)|=1」となるように,減衰分を非反転増幅器で増幅しなければなりません.このときのゲインよりR4を計算すると求まります.「|G(jω)β(jω)|=1」の条件は,バルクハウゼン基準(Barkhausen criterion)と呼びます.
正弦波の発振回路は水晶振動子やセミック発振子,コイルとコンデンサを使った回路などがありますが,これらは高周波の用途で,低周波には向きません.低周波の正弦波発振回路はウィーン・ブリッジ発振回路などのOPアンプ,コンデンサ,抵抗で作るCR型の発振回路が向いており抵抗で発振周波数を変えられるメリットもあります.ウィーン・ブリッジ発振回路は,トーン信号発生や低周波のクロック発生などに使われています.
図1のウィーン・ブリッジ発振回路が発振するためには,正帰還のループ・ゲインが1倍のときです.ループ・ゲインは帰還率(β)と非反転増幅器のゲイン(G)の積となります.|Gβ|=1とする非反転増幅器のゲインを求め,R3は10kΩと決まっていますので,非反転増幅器のゲインの式よりR4を計算すれば求まります.まず,図1の抵抗(R1,R2)が10kΩ,コンデンサ(C1,C2)が0.01μFを用い,周波数(ω)が「1/CR=10000rad/s」でのRC直列回路とRC並列回路のインピーダンスを計算し,|β(s)|を求めます.
R1とC1のRC直列回路のインピーダンスZaは,式1であり,その値は式2となります.
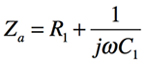 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
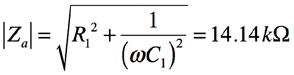 ・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・(2)
次にR2とC2のRC並列回路のインピーダンスZbは式3であり,その値は式4となります.
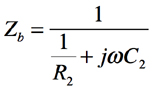 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
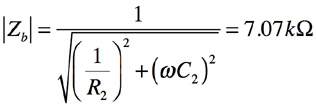 ・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・(4)
帰還率βは,|Za|と|Zb|より,式5となります.
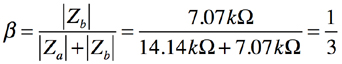 ・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・(5)
式5より「ω=10000rad/s」のときの帰還率は「|β|=1/3」となり,減衰しています.したがって,|Gβ|=1とするには,式6の非反転増幅器のゲインが必要となります.
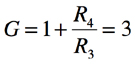 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式6でR3は10kΩであることから,R4が20kΩとなります.
●正帰還の発振回路はループ・ゲインと位相が重要
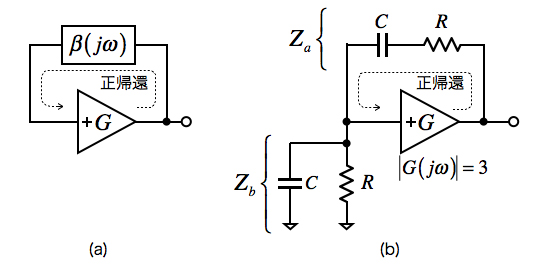
図2(a)は発振回路のブロック図で,図2(b)がウィーン・ブリッジ発振回路の等価回路図です.正帰還を使う発振回路は,正帰還ループのループ・ゲインと位相が重要です.図2(a)で正弦波の発振を持続させるためには,ループ・ゲインが1倍で,位相が0°の場合,正弦波の発振条件になるからです.
図2(a)の帰還率β(jω)の具体的な回路が,図2(b)のRC直列回路とRC並列回路に相当します.また,Gのゲインを持つ増幅器は,図1のOPアンプとR3,R4からなる非反転増幅器です.このようにウィーン・ブリッジ発振回路は,正弦波出力となるように正帰還を調整した発振回路です.
●ウィーン・ブリッジ発振回路の発振周波数と非反転増幅器のゲインを計算する
解答では,具体的なインピーダンス値を使って求めましたが,ここでは一般式を用いて解説します.図2(b)のウィーン・ブリッジ発振回路の等価回路図で,正帰還側の帰還率β(jω)は,RC直列回路のインピーダンス「Za=R+1/jωC」と.RC並列回路のインピーダンス「Zb=R/(1+jωCR)」より,式7となり,整理すると式8となります.
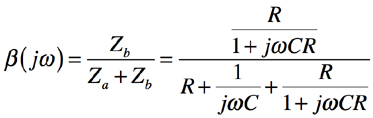 ・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・(7)
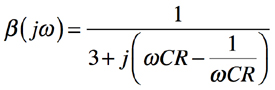 ・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・(8)
β(jω)の周波数特性を図3に示します.
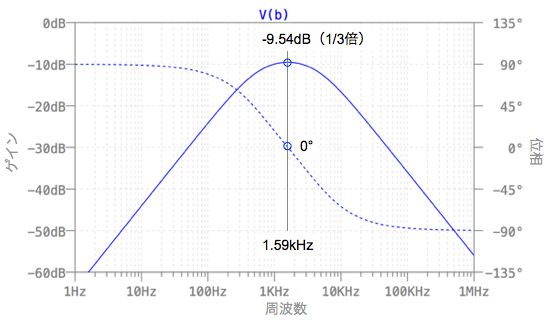
中心周波数のゲインが1/3倍,位相が0°
帰還率β(jω)は,「ハイ・パス・フィルタ(HPF)」と「ロー・パス・フィルタ(LPF)」を組み合わせた「バンド・パス・フィルタ(BPF)」としての働きがあります.BPFの中心周波数より十分低い周波数の位相は,+90°であり,十分高い周波数の位相は-90°です.この間を周波数に応じて位相シフトします.式7において,BPFの中心周波数(ω)が「1/CR」のときの位相を確かめると,虚数部がゼロになり,ゆえに位相は0°となります.このときの帰還率のゲインは「|β(jω)|=1/3」となります.これは図3でも確認できます.また,発振させるためには「|G(jω)β(jω)|=1」が条件ですので,式6のように「G=3」が必要であることも分かります.
以上の特性を持つBPFが正帰還ループに入るため,ウィーン・ブリッジ発振器は「|G(jω)β(jω)|=1」かつ,位相が0°となるBPFの中心周波数(ω)が「1/CR」で発振します.また,ωは2πfなので「f=1/2πCR」となります.
●ウィーン・ブリッジ発振回路をLTspiceで確かめる
図4は,図1のウィーン・ブリッジ発振回路をシミュレーションする回路で,R4の抵抗値を変数にし「.stepコマンド」で10kΩ,20kΩ,30kΩ,40kΩを切り替えています.
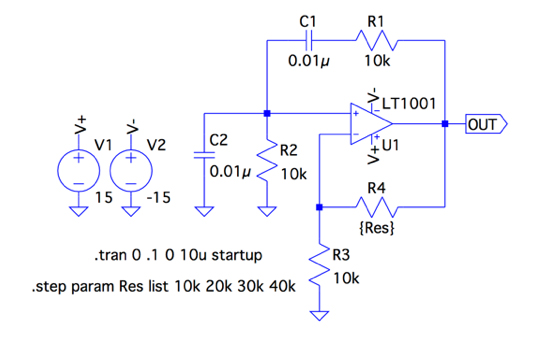
R4の抵抗値を変数にし,4種類の抵抗値でシミュレーションする
図5は,図4のシミュレーション結果です.10kΩのときは非反転増幅器のゲイン(G)は2倍ですので「|G(jω)β(jω)|<1」となり,発振は成長しません.20kΩのときは「|G(jω)β(jω)|=1」であり,正弦波の発振波形となります.30kΩ,40kΩのときは「|G(jω)β(jω)|>1」となり,正帰還量が多いため,発振は成長し続けやがて,OPアンプの最大出力電圧で制限がかかり波形は歪みます.
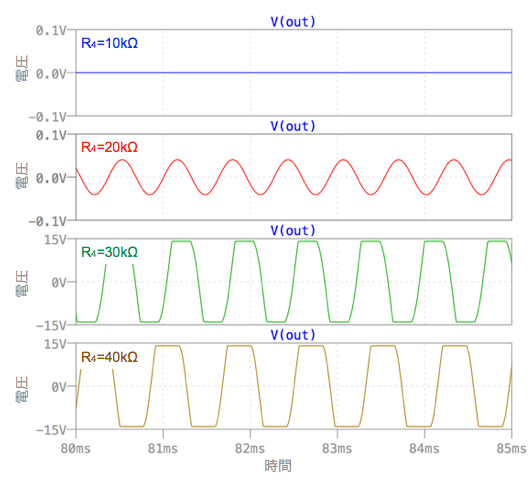
20kΩのとき正弦波の発振波形となる.
図4の回路で過渡解析の時間を2秒まで増やしたシミュレーション結果が図6です.このように長い時間でみると,発振は収束しています.原因は,先ほどの計算において,OPアンプを理想としているためです.非反転増幅器のゲインを微調整して,正弦波の発振を継続するのは意外と難しいため,回路の工夫が必要となります.この対策回路はいろいろなものがありますが,ここでは非反転増幅器のゲインを自動で調整する例について解説します.

長い時間でみると,発振は収束している.
●AGC付きウィーン・ブリッジ発振回路
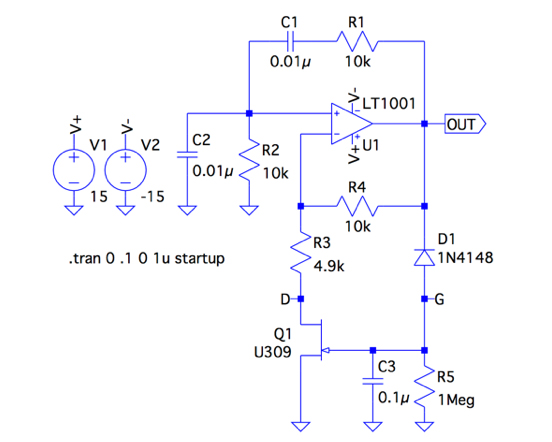
図7は,ウィーン・ブリッジ発振回路のゲインを,発振出力の振幅を検知して自動でコントロールするAGC(Auto Gain Control)付きウィーン・ブリッジ発振回路の例です.ここでは動作が理解しやすいシンプルなものを選びました.
図4と図7の回路を比較すると,図7は新たにQ1,D1,R5,C3を追加しています.Q1はNチャネルのJFET(Junction Field Effect Transistor)で,VGSが0Vのときドレイン電流が最大で,VGSの負電圧が大きくなるほど(VGS<0V)ドレイン電流は小さくなります.このドレイン電流の変化は,ドレイン-ソース間の抵抗値(RDS)の変化にみえます.したがって非反転増幅器のゲイン(G)は「1+R4/(R3+RDS)」となります.Q1のゲート電圧は,D1,R5,C3により,発振出力を半坡整流し平滑した負の電圧です.これにより,発振振幅が小さなときは,Q1のRDSは小さく,非反転増幅器のゲインは「G>3」となって発振が早く成長するようになり,反対に発振振幅が成長して大きくなると,RDSが大きくなり,非反転増幅器のゲインが下がりAGCとして動作します.
●AGC付きウィーン・ブリッジ発振回路の動作をシミュレーションで確かめる
図8は,図7のシミュレーション結果で,ウィーン・ブリッジ発振回路の発振出力とQ1のドレイン-ソース間の抵抗値とQ1のゲート電圧をプロットしました.発振出力振幅が小さいときは,Q1のゲート電圧は0V付近にあり,Q1は電流を流すことから,ドレイン-ソース間の抵抗RDSは約50Ωです.この状態の非反転増幅器のゲイン(G)は「1+10kΩ/4.95kΩ」の3.02倍で発振が成長します.発振出力振幅が安定したときは,RDSは約100Ωで,非反転増幅器のゲイン(G)は3倍となります.
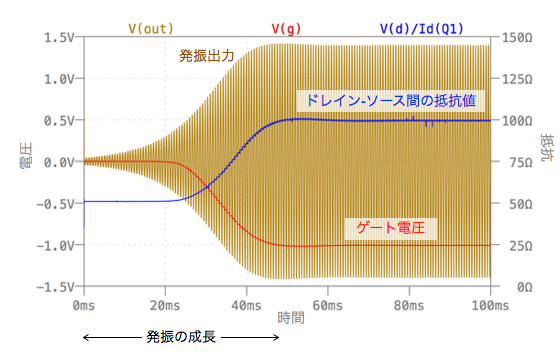
図9は,図8の発振出力の80msから100ms間をフーリエ変換した結果です.発振周波数は10kΩと0.01μFで設定した「f=1/(2π*10kΩ*0.01μF)=1.59kHz」であることが分かります.
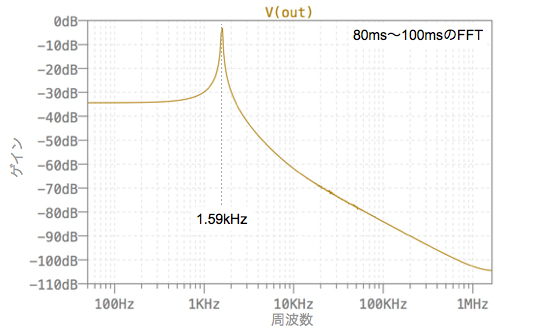
発振周波数は10kΩと0.01μFで設定した1.59kHzであることが分かる.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_036.zip
●データ・ファイル内容
Wein_Bridge_Oscillator.asc:図4の回路
Wein_Bridge_Oscillator_with_AGC.asc:図7の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










