トランスコンダクタンス・フィルタのカットオフ周波数はいくつ?

図1は,トランスコンダクタンス(Transconductance)・アンプを使用した1次のローパス・フィルタです.Q1,Q2のエミッタに接続された電流源の電流を520μAとし,Q9のベースに接続されたコンデンサ(C1)の容量値を160nFとしたとき,この回路のカットオフ周波数として,もっとも近いのは(A)~(D)のどれでしょうか.ただし,入力される信号は,小さく10mVrms以下とします.
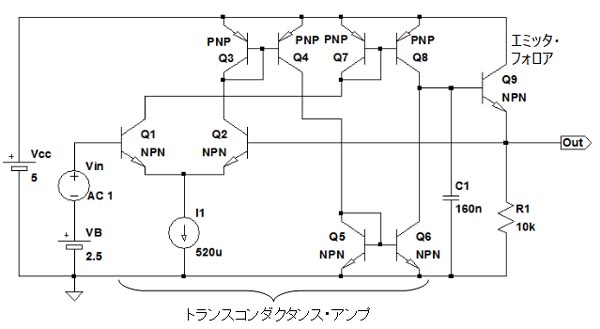
この回路のカットオフ周波数は?
図1の回路のカットオフ周波数(f)は,差動増幅回路の相互コンダクタンス(gm)とC1で決まり「f=gm/2*π*C」で表されます.また,差動増幅回路のgmはI1に比例します.I1からgmを求めればカットオフ周波数を求めることができます.
トランスコンダクタンス・アンプを使用したフィルタは電流によってカットオフ周波数を変えることができるため,電圧によって電流をコントロールする回路を追加し,VCF(Voltage-controlled filter)を構成することができます.VCFは,電子楽器のアナログ・シンセサイザーなど,いろいろなところで使用されています.
図1の差動増幅回路のgmは「gm=I1/2*VT=260u/26m=10m[S]」です.このgmの値を使用してカットオフ周波数を求めると「f=gm/2*π*C=10m/2*π*160n=9.95[kHz]」となります.この値に一番近いのは(C)の10kHzなので,正解は(C)ということになります.
●トランスコンダクタンス・フィルタの伝達関数を計算する
図2は,図1の回路をブロック図に書き換えたものです.図1では出力とトランスコンダクタンス・アンプの反転入力端子は直結されていますが,図2では汎用性を持たせるため,帰還経路にHという係数を挿入しています.
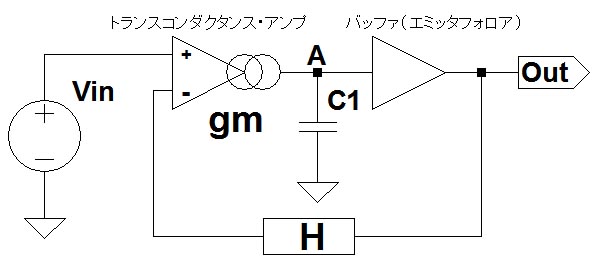
汎用性を持たせるため,帰還経路にHという係数を挿入.
図2でA点の電圧は,トランスコンダクタンス・アンプの出力電流と,C1のインピーダンスを掛け合わせたものです.また,トランスコンダクタンス・アンプの出力電流は+入力端子と-入力端子の差電圧にgmを掛けたものです.バッファのゲインが1倍のため,A点の電圧(VA)とOut端子の電圧(VOut)は同じになります.トランスコンダクタンス・アンプの反転入力端子には「VOut*H」という電圧が入力されます.これらの関係から式を立てると式1になります.
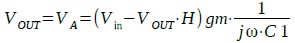 ・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・(1)
式1をVOutについて解くと,式2になります.
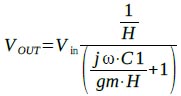 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
図1の回路でHは1なので,式2でH=1とすると式3になります.
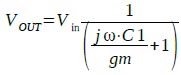 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3は,一次のローパスフィルタの伝達関数と同じ形なので,時定数(ωT)がC1/gmとなります.したがってカットオフ周波数(f)は式4になります.
 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
●回路の周波数特性をLTspiceで確認する
図3は,図1の回路の周波数特性をシミュレーションするための回路です.

10Hzから1MHzまでの周波数特性をシミュレーションする
図3の回路でQ3,Q4とQ5,Q6およびQ7,Q8はそれぞれカレント・ミラーを構成しています.差動対トランジスタQ2のコレクタ電流は,Q3,Q4のカレント・ミラーを経由し,Q5,Q6のカレント・ミラーによってA点に出力されます.また,Q1のコレクタ電流はQ7,Q8のカレント・ミラーによってA点に出力されます.したがって,入力からA点までのgmは式5で表すことができます.
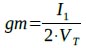 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式4に式5のgmを代入すると式6になります.
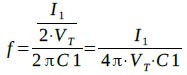 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
ただし,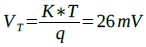 K:ボルツマン定数,T:絶対温度,q:電子電荷とする
K:ボルツマン定数,T:絶対温度,q:電子電荷とする
式6に図3の定数を代入すると,式7のようにカットオフ周波数は9.95kHzになります.
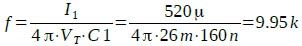 ・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・(7)
図4は,図3のシミュレーション結果です.カットオフ周波数が約9.5kHzとほぼ計算通りの値となっています.
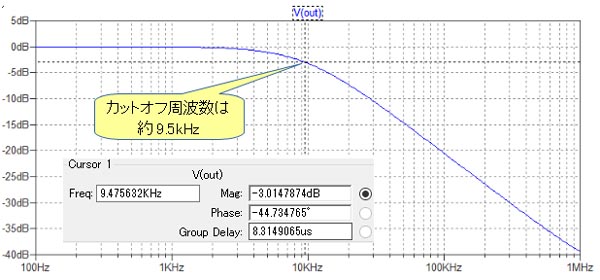
カットオフ周波数は約9.5kHzとほぼ計算通り.
式6で重要なのが,カットオフ周波数が電流I1で変化することです.図1の回路は,I1を可変することで,カットオフ周波数を可変することのできるフィルタになります.
図5は,図3の回路のI1を130μ,260μ,520μ,1.04m,2.04mと変化させたときの周波数特性です.電流値に応じてカットオフ周波数が変わっていることがわかります.
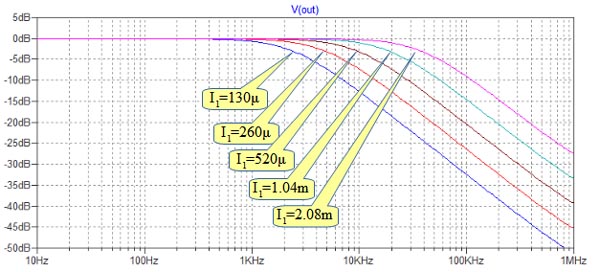
電流値に応じてカットオフ周波数が変わっていることがわかる.
●帰還量を変えたときの周波数特性をシミュレーションする
図6は,出力からトランスコンダクタンス・アンプの反転入力端子への帰還量を,R2,R3の抵抗分割によって変えたものです.帰還量は図2のHに相当するもので,式8のようにH=0.1となります.
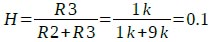 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
ここで,式2にH=0.1を代入すると式9になり,これが図6の伝達関数になります.
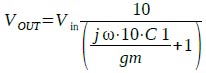 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
式9からわかるように,図6の回路は,図3の回路に比べ,全体のゲインが10倍になり,時定数(ωT)も10倍になっています.時定数が10倍になっているため,カットオフ周波数は1/10になります.図3の回路のカットオフ周波数が約9.5kHzだったため,図6の回路のカットオフ周波数は約950Hzに低下することになります.
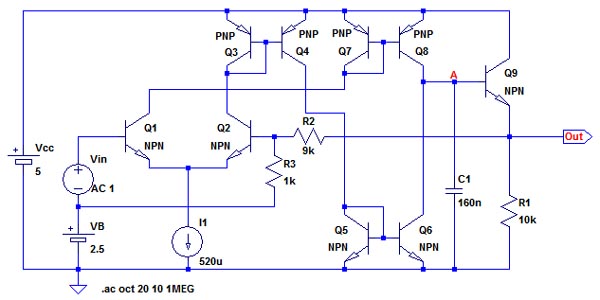
R2,R3の抵抗分割で帰還量を減らしている.
図7は,図6の回路のシミュレーション結果です.ほぼ計算通り,低域のゲインは20dB(10倍)となり,カットオフ周波数は,図4の約1/10の900Hzになっていることがわかります.
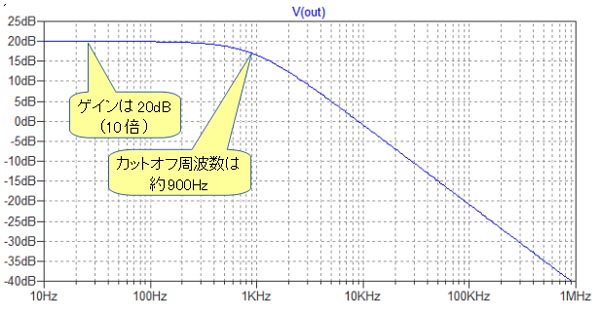
ほぼ計算通り,ゲイン10倍,カットオフ周波数1/10になっている.
図3の回路は,カットオフ周波数よりも高い周波数で大きな信号(100mVPP以上)が入力されると,Q1,Q2の差動トランジスタの入力許容範囲を越え,所望のフィルタ動作をしなくなります.そのため,入力に抵抗分割によるアッテネータを挿入して入力信号を減衰させ,帰還回路は図6のようにしてゲインを持たせることで,全体のゲインを1とするような使い方をすることがあります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_033.zip
●データ・ファイル内容
t-conductanceFil.asc:図3の回路
t-conductanceFil_step.asc:図5をシミュレーションするための回路
t-conductanceFil2.asc:図6回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










