温度による出力電圧の変化が最も小さい抵抗値はいくつ?

図1は,バンド・ギャップ・リファレンスと呼ばれる基準電圧源の回路図です.トランジスタQ1,Q2,Q3,Q4の特性は同じで,温度も等しく,また,抵抗の温度係数は無視できるものとします.この回路で周囲温度を-25℃から75℃に変えた場合,温度による出力電圧の変化(温度係数)が最も小さいR3の抵抗値は,(A)~(D)の中のどれでしょうか.
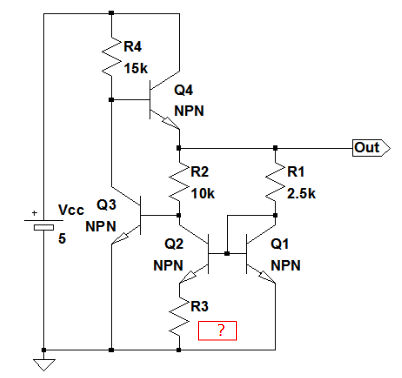
温度による出力電圧変化の小さいR3の抵抗値は?
図1の回路において,温度による出力電圧の変化が小さいのは,出力電圧を1.262Vにしたときです.R3を変えることで出力電圧が変わります.そのため,出力電圧が1.262Vに一番近くなるR3の値を選べばよいことになります.
図1の回路において,R1とR2の抵抗比が4:1なので,Q1のコレクタ電流はQ2のコレクタ電流の4倍になります.そのため,Q2のコレクタ電流(ICQ2)は「ICQ2=(VT*ln(4))/R3」で計算することができます.Q1の電流(ICQ1)は「ICQ1=4*ICQ2」となるので,出力電圧(VOUT)の概算値は式1で計算することができます.
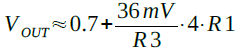 ・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1を使用して,温度による出力電圧の変化が小さい「VOUT=1.262V」になるR3の値を計算すると,式2のように640Ωになります.
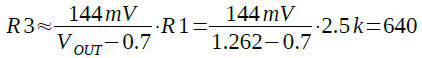 ・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・(2)
(A)~(D)でこの値に最も近いのは(B)の720Ωです.そのため,正解は(B)ということになります.
●バンド・ギャップ・リファレンス回路の動作
図1のバンド・ギャップ・リファレンス回路の動作はやや難解ですが,各トランジスタの役割とともに,順番に解説していきます.図2は,図1の回路の動作を理解しやすくするために,回路の一部を取り出し,書き換えたものです.Q4のかわりに電圧源V1が配置されています.Q3は単純なダイオードに書き換え,さらに「NPN 0.25」として,1/4サイズのトランジスタとしてあります.また,R3は解答で求めた720Ωにしました.
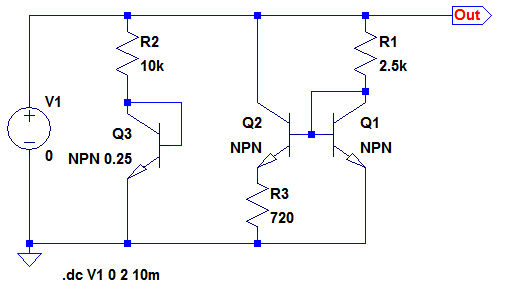
Q4はV1に置き換え,Q2,Q3の接続も変更してある.
図3は,図2でV1の値を変えたときのシミュレーションを行い,Q2のコレクタ電流とR2の電流をプロットしたものです.Q1とQ2はカレント・ミラーとして動作しますが,R3があることによって,Q1の電流が増えてもQ2のコレクタ電流がリニアに増加することはありません.そのため,図2の定数では,OUT端子の電圧が,1.23V(1.262Vの近似値)より低いときは,Q2のコレクタ電流がR2に流れる電流よりも大きくなっています.1.23Vを越えるとR2の電流のほうが大きくなります.
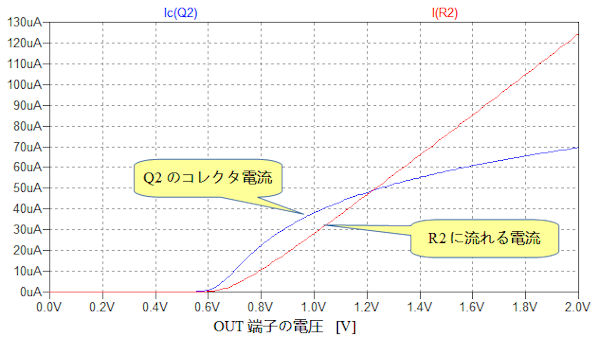
1.23V以下ではQ2のコレクタ電流のほうが多い.
●バンド・ギャップ・リファレンス回路の動作をLTspiceで確認する
図4は,図1の回路をシミュレーションするための回路図です.ここでも,R3は解答で求めた720Ωにしています.
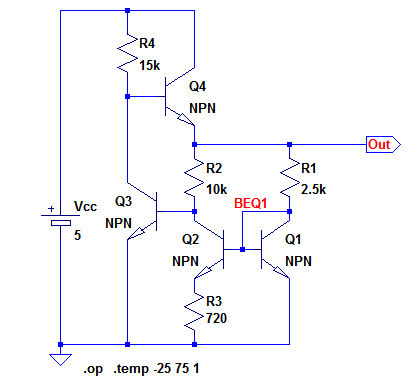
図4において,Q4はエミッタ・フォロアとして動作し,R1とR2に等しい電圧を供給します.Q3はR2の電流とQ2の電流が等しくなるように,Q4を介してOUT端子の電圧を制御する働きをしています.
OUT端子の電圧が低いときは図3のように,Q2のコレクタ電流のほうがR2の電流よりも大きいため,Q3のベース電圧が低くなります.すると,Q3のコレクタ電流が流れないので,Q4のベース電圧が高くなります.それによって,OUT端子の電圧が上昇します.
OUT端子の電圧が一定の電圧を越えるとR2の電流のほうが大きくなります.するとQ3のベース電圧が高くなり,Q3のコレクタ電流が増えます.それによって,Q4のベース電圧が下がり,OUT端子の電圧も下がります.このようにして,バンド・ギャップ・リファレンス回路のOUT端子の電圧は,「特定の電圧」で落ち着くことになります.
●バンド・ギャップ・リファレンス回路の出力電圧を求める式
次にバンド・ギャップ・リファレンス回路の出力電圧を求める式について解説します.「特定の電圧」に落ち着くのは,R2の電流とQ2の電流が等しくなったときです.ここで,Q1のベース・エミッタ間電圧(VBE)とQ3のVBEがほぼ等しいと仮定します.すると,R1とR2に加わる電圧は等しくなります.R2の抵抗値はR1の4倍に設定されているため,R1の電流はR2の電流の4倍になります.ベース電流を無視するとR1の電流とQ1のコレクタ電流は同じです.また,R2の電流とQ2のコレクタ電流も等しくなっています.そのため,Q1のコレクタ電流はQ2のコレクタ電流の4倍になります.Q1とQ2のVBEはそれぞれ式3,式4で表されます.
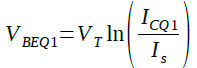 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
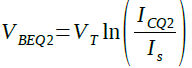 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
ただし,VT=K*T/q=26mV K:ボルツマン定数,T:絶対温度,q:電子電荷
Q2のコレクタ電流のほうが少ないため,VBEも小さくなり,Q1とQ2のVBEの差電圧(ΔVBE)がR3に加わる電圧となります.差電圧ΔVBEは式5で計算できます.
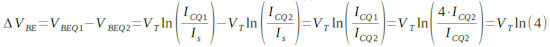 ・・・・・(5)
・・・・・(5)
Q2のコレクタ電流(≒エミッタ電流)は式5の結果を使い,式6のようになります.
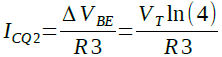 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
OUT端子の電圧(VOUT)はQ1のVBEとR1の電圧降下を足し合わせたものなので,式7で表されます.
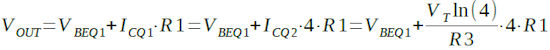 ・・・・・(7)
・・・・・(7)
VBEQ1を0.7Vとして式7を書き換えると式8のようになります.
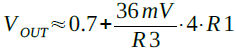 ・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式8は式1と同じです.なので,R3に720Ω,R1に2.5kΩを代入すると1.262Vの近似値が得られます.式7を見ると式の第一項はVBEで,マイナスの温度係数を持った電圧です.第二項はVTに比例した値でプラスの温度係数を持っています.この両者を適切な比率で加算すれば,「特定の電圧」で温度による出力電圧の変化(温度係数)を小さくできることが分かります.
図5は,図4のシミュレーション結果です.式7のようにマイナスの温度係数を持つVBEQ1とプラスの温度係数を持つR1の電圧を加算することで,温度による出力電圧(V(OUT))の変化(温度係数)が小さくなっていることがわかります.
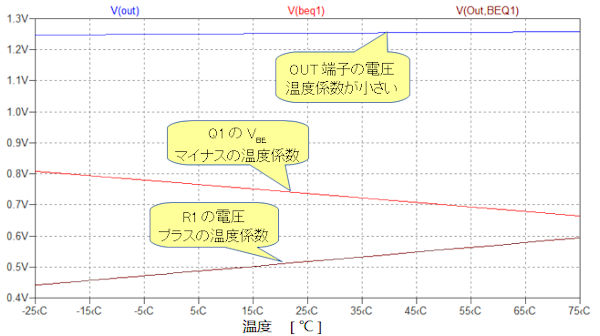
マイナスとプラスの温度係数の電圧の加算で温度係数が小さくなっていることがわかる.
●温度係数が最も小さくなる1.262Vとは
ヒントにも記載したように図1の回路で出力電圧の温度係数が最も小さくなるのは,OUT端子の電圧を1.262Vにしたときです.1.262Vの算出過程は省略しますが,25℃での温度係数が最も小さくなる電圧は,式9のようにシリコンの物理定数であるバンド・ギャップ電圧(1.205V)に,25℃での熱電圧VT(26mV)を2.2倍したものを加算したものになります.
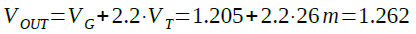 ・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・(9)
実際の設計ではこの電圧を目安に,最も温度係数が小さくなるように,R3の値などを微調整することになります.
●温度特性をシミュレーションする
図6は,図1の回路でR3の値を変えたときの温度特性をシミュレーションするための回路です.「.step」でR3の抵抗値を360Ω,720Ω,1440Ω,2880Ωと変化させています.
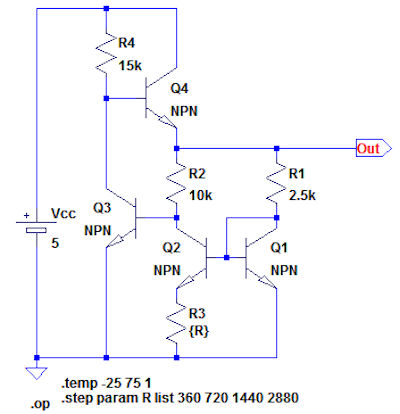
R3の抵抗値を360Ω,720Ω,1440Ω,2880Ωと変化させている
図7は,図6のシミュレーション結果です.R3の値を720Ωとしたとき,温度による出力電圧の変化が一番小さくなっています.
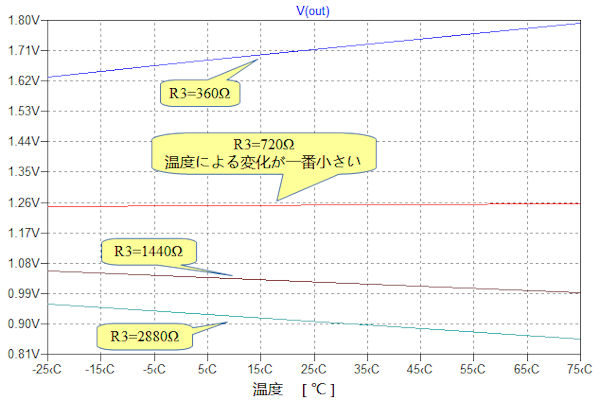
R3=720Ωのときが,温度による出力電圧の変化が小さい
図1の回路は電源電圧を変えるとQ3のコレクタ電流が変化します.Q3のコレクタ電流が変化することで,Q3のVBEも多少変化するため,出力電圧も若干変化してしまいます.そのため,電源電圧依存性を小さくする改良を加えたものなど,さまざまなバンド・ギャップ・リファレンスが考案され,使用されています.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_031.zip
●データ・ファイル内容
bandgap0.asc:図2の回路
bandgap1.asc:図4の回路
bandgap2.asc:図6の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










