ハウランド電流ポンプから負荷へ流れる電流はいくら?

図1は,ハウランド電流ポンプ(Howland Current Pump)と呼ばれる電圧制御電流源です.1個のOPアンプ(LT1001)と4個の抵抗から構成されています.抵抗の値は,R1,R2,R3,R4全て10kΩです.この回路は,入力電圧(VIN+)に応じた電流(IL)をグランウドに接続した100Ωの負荷抵抗(RL)へ流す働きをします.入力電圧(VIN+)が1Vのとき,負荷抵抗(RL)に流れる負荷電流(IL)は(a)~(d)のうちどれでしょうか.

1個のOPアンプと4個の抵抗から構成されている.
図1は「R2/R1」と「R4/R3」の抵抗比が同じであり,OPアンプの非反転端子と反転端子への帰還量は同じです.また,OPアンプの非反転端子と反転端子はバーチャル・ショートであり,その電圧はVOとなります.上記の条件においてR1に流れる電流をI1,R2に流れる電流をI2とすれば,負荷電流ILは「IL=I1+I2」として求められます.
電圧制御電流源の用途として,テスタを使用してデバイスを測定するときの正と負の電流源や測温抵抗体(RTD)への電流印加,また,直流信号の伝送規格である4~20mAのカレント・ループなどがあります.
図1の抵抗R1,R2,R3,R4をRとして,OPアンプの出力端子の電圧をVa,バーチャル・ショートの電圧をVOとすれば式1になります.
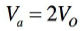 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また,負荷抵抗に流れる電流をIL,R1に流れる電流をI1,R2に流れる電流をI2とすれば式2になります.
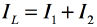 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
式2のI1とI2を図1の電圧と抵抗で表せば式3になります.
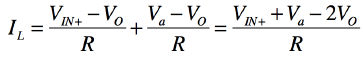 ・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・(3)
式3へ式1を代入すれば式4になります.
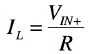 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4に「VIN+=1V」,「R=10kΩ」を代入すれば,ILは100μAとなり,解答は(c)となります.
●ハウランド電流ポンプは抵抗比を合わせることが重要
図1の回路で「R1=R2=R3=R4=R」とすれば,式4のように電圧を電流に変換するゲインは「1/R」となります.また,式4の負荷電流(IL)は,ハウランド電流ポンプの出力電圧VOの項がありません.したがって,入力電圧が一定であれば,出力電圧によって負荷電流が変化しない,定電流源となります.
ここで,図1を使い,出力電圧に依存しない電流源となる条件について考察します.図1において,非反転端子と反転端子はバーチャル・ショートですのでVaは式5となります.
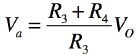 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
また,キルヒホッフの法則より式6の関係があります.
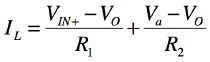 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式6へ式5を代入して整理すると,負荷電流(IL)は式7となります.
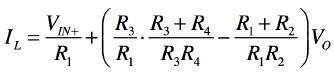 ・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・(7)
式7より,出力電圧VOに依存しない条件は,右辺第2項がゼロとなるときです.すなわち,右辺第2項の小括弧内をゼロとすればよくて,その条件は「R2/R1=R4/R3」になります.また,このときの負荷電流は「IL=VIN+/R1」となります.このようにハウランド電流ポンプは「R2/R1=R4/R3」となるように抵抗比をあわせることが重要です.
●ハウランド電流ポンプをLTspiceで確かめる
図2は,図1をシミュレーションする回路です.OPアンプの電源は±15V,入力電圧は-5Vから+5Vまで10mVステップで増加させ,負荷抵抗に流れる電流をシミュレーションします.また,負荷抵抗に依存しない(前述の出力電圧「VO=IL*RL」に依存しない)ことを確かめるために負荷抵抗を「.stepコマンド」で10Ω,100Ω,1kΩと変化させています.
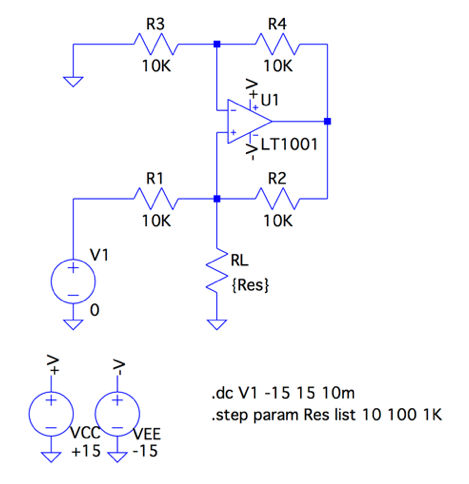
負荷抵抗RLを10Ω,100Ω,1kΩと変化させている.
図3が図2のシミュレーション結果です.まず,負荷電流が「V1=1V」のとき,100μAであり解答と同じであることが確かめられました.負荷抵抗を10Ω,100Ω,1kΩと変化させてもグラフは重なっており,負荷電流は変わりません.また,接地した負荷に対し正と負の電流を流しており,両方向の電圧制御電流源として動作することも分かります.
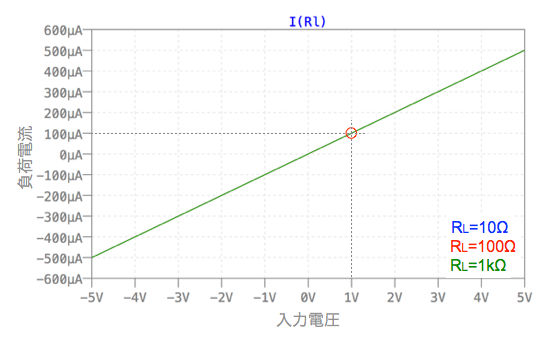
負荷電流が「V1=1V」のとき,100μAであることが確かめられる.
●改良型の電圧制御電流源
ハウランド電流ポンプは入力電圧(VIN+)とR1で負荷電流を制御していました.この場合,負荷電流を小さくするとき,小さなVIN+の電圧,あるいは,大きな値のR1が必要となります.R1を大きくするとR2,R3,R4も大きくなります.
図4は,ハウランド電流ポンプを改良した電圧制御電圧源で,ボルテージ・フォロワ回路をR2と負荷抵抗(RL)の間に入れ,負荷電流がR2側へ流れないようにした回路です.この変更により,R1,R2,R3,R4を大きな値にしなくてもよく,負荷電流は,抵抗R5で制御できるようになります.
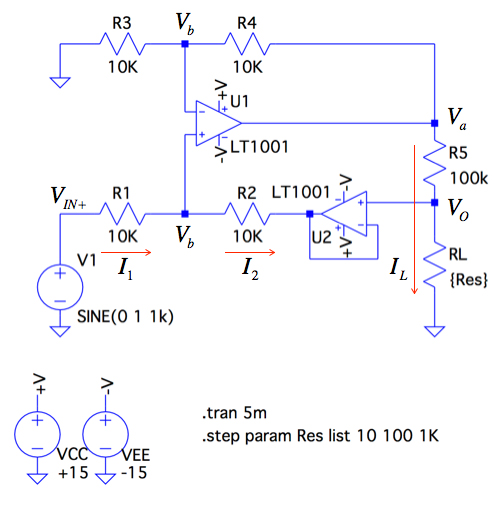
ボルテージ・フォロワ回路をR2と負荷抵抗(RL)の間に入れている.
図4の負荷電流(IL)が負荷抵抗に依存しない(出力電圧「VO=IL*RL」に依存しない)関係と,そのときの負荷電流を求めます.まず,図4は,式8~式11の関係があります.
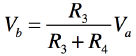 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
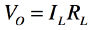 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
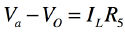 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
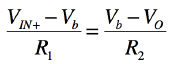 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
これらより,式12が求まります.
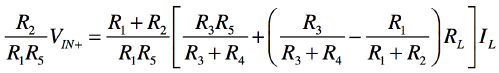 ・・・・・・・・(12)
・・・・・・・・(12)
式12より,負荷電流が負荷抵抗に依存しない電流源となるためには,右辺の小括弧内がゼロとなるように「R3/(R3+R4)=R1/(R1+R2)」の関係にする必要があります.小括弧内がゼロとするには「R2/R1=R4/R3」とすればよいことが分かります.このときの負荷電流は,式13となり,R5で制御できることが分かります.
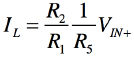 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
図5は,図4のシミュレーション結果です.図4では,V1へ振幅1V,周波数1kHzの正弦波を印加しています.また,図2と同様に負荷抵抗を「.stepコマンド」で10Ω,100Ω,1kΩと変化させ,過渡解析を用いました.
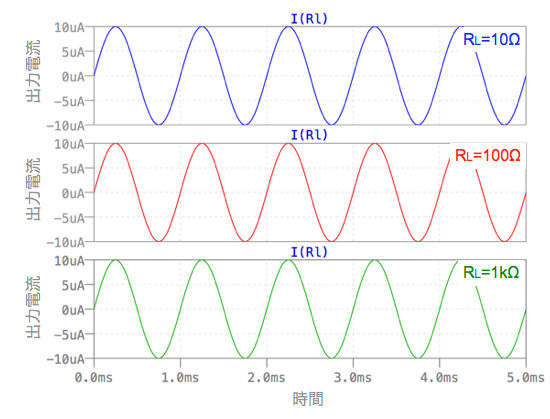
「R1=R2=R3=R4=10kΩ」,「R5=100kΩ」,「V1=1V」の条件では,式13より「IL=10μA」となります.図5のシミュレーション結果でも負荷電流のピーク値は,10μAとなっていることが確かめられました.また,接地した負荷に対し正と負の電流を流しており,両方向の電圧制御電流源として動作することも分かります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_030.zip
●データ・ファイル内容
Howland.asc:図2の回路
VOtgate_Controlled_Current_Source.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










