コルピッツ発振回路の発振周波数を表す式は?

図1は,ベース接地・トランジスタを使用したコルピッツ発振回路です.コイルL1のインダクタンスの値をL1とし,コンデンサC1,C2のキャパシタンスの値をC1,C2とすると,このコルピッツ発振回路の発振周波数を表す式として,もっとも適切なのは(A)~(D)のどれでしょうか.
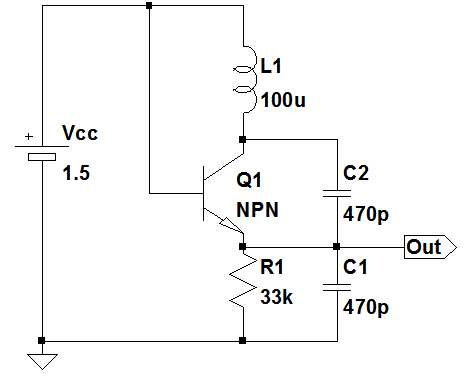
この回路の発振周波数を表す式は?
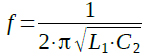
(B)
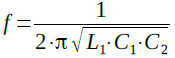
(C)
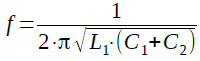
(D)
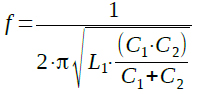
コルピッツ発振回路は,コイルとコンデンサから構成された並列共振回路の共振周波数で発振します.図1の回路において,電源は交流的にはグラウンドと等価として考えることができます.電源をグラウンドと考えたとき,どのように並列共振回路が構成されるかを考えれば,答えが分かります.
図1において電源を交流的なグラウンドと考えると,コンデンサC1の下側を電源に接続しても同じ動作をします.図2は,コイルとコンデンサから構成される並列共振回路を分かりやすくするため,C1の下側を電源に接続して,図1の回路を書き換えたものです.
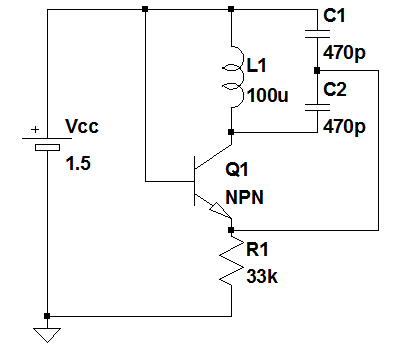
L1にはC1,C2を直列接続したものが並列に接続されている.
図2を見ると,コイルL1にはC1,C2を直列接続したものが並列に接続されています.C1とC2を直列接続したときの合成容量(C)は,式1で表されます.
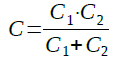 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
共振周波数(f)は,この合成容量を使って式2で計算することができます.
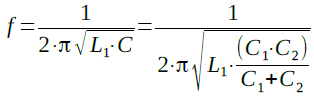 ・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・(2)
式2は,(D)と同じです.コルピッツ発振回路はこの共振周波数で発振するので,正解は(D)ということになります.なお,具体的な数値を入れて計算すると式3のように1.038MHzになります.
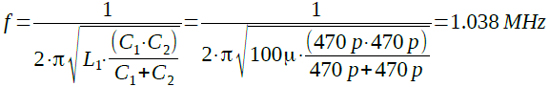 ・・・・・(3)
・・・・・(3)
●フィードバック回路の発振条件
コルピッツ発振回路の仕組みについて考える前に,一般的なフィードバック回路の発振条件について確認しておきます.図3は,一般的なフィードバック回路をブロック図で表したものです.
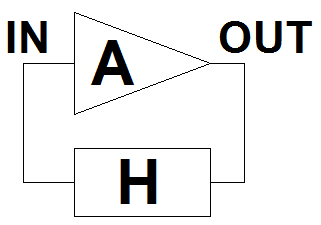
発振条件はA*H>1で,帰還信号の位相が入力と同位相であること.
このようなフィードバック回路が発振するためには二つの条件を満たしている必要があります.まず,帰還される信号(OUT*H)の位相が入力と同じ位相であり,かつ帰還される信号が入力した信号よりも大きいこと(帰還ゲインが1以上 A*H>1)です.
●コルピッツ発振回路の帰還ゲインの計算
コルピッツ発振回路が発振する仕組みを考えるために,図4のX印のところで回路を切断して動作を考えます.この回路ではトランジスタはベース接地増幅回路として動作し,入力はエミッタで出力はコレクタです.コレクタの出力をC2とC1で分圧し,その出力が再び入力のエミッタに帰還されていると考えることができます.
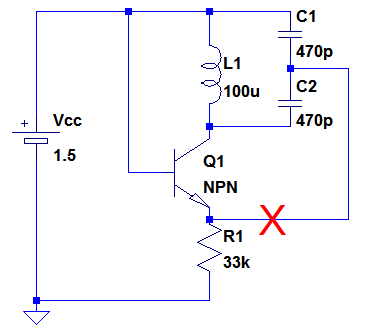
X印のところを切断して動作を考える.
図5は,図4の回路が先ほど示した発振条件を満たしているかを考えるための回路です.
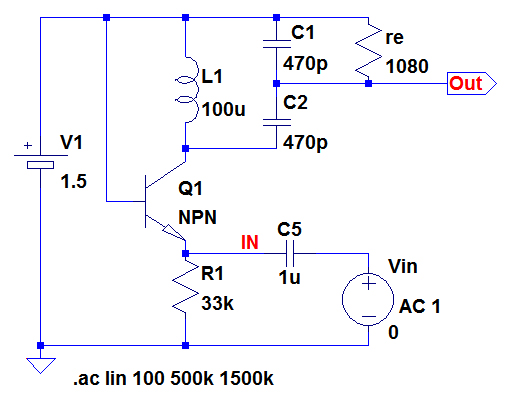
ループ切断前とゲインを合わせるため,reを挿入している.
図5は,図4の回路をX印のところで切断し,エミッタに入力信号を加えています.C1に並列に接続されている抵抗(re)はQ1のエミッタの入力抵抗です.回路を切断してもゲインが同一になるように,C1に並列に接続しています.図4においてトランジスタQ1のエミッタ電流(IE)は式4で計算できます.
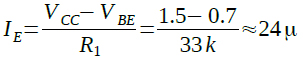 ・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・(4)
Q1のエミッタの入力抵抗reはこのエミッタ電流を使って式5ように1080Ωと計算できます.
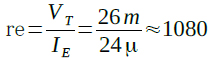 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
そのため,図5のreは1080Ωとしてあります.この回路のINからOUTまでのゲインが1以上で,位相が同一であれば,図4の回路は発振することになります.
図5の回路のゲインを手計算するためには,OUT端子の等価インピーダンスを求める必要があります.やや煩雑な計算が必要になります.そこで,ここでは図5の共振回路の部分を図6のように変形して簡易的にゲインを計算します.
図6の右のように変形すると,この回路の並列共振周波数でのインピーダンスは「4*re」となります.Out端子の電圧はC1,C2で分圧されるため,コイル両端の電圧の半分になります.そのためOut端子の並列共振周波数での等価インピーダンスは「2*re」と考えることができます.
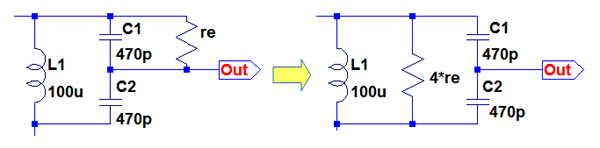
Out端子の並列共振周波数での等価インピーダンスは「2*re」.
ベース接地増幅回路のゲイン(G)はコレクタ電流をICとし,負荷抵抗をRLとすると式6で計算できます.
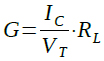 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
図5において,Out端子の並列共振周波数での等価インピーダンスは「2*re」であり,これが式6の負荷抵抗(RL)に相当します.式4においてhfeが十分大きく「IC=IE」とすると,式6は式7のように変形できます.
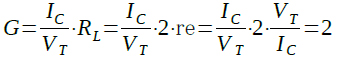 ・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・(7)
式7より,図5の回路は,2倍のゲインを持っていることが分かります.非常に面白いことに,このゲインはトランジスタの電流に依存しません.また,並列共振周波数では共振回路は純抵抗とみなせ,ベース接地増幅回路の出力信号は入力信号と同位相となることから,図4の回路は発振条件を満たしていることが分かります.
●コルピッツ発振回路のシミュレーション
図7は,図5の回路のシミュレーション結果です.位相が0度となっている周波数は1.038MHzでその時のゲインは6.3dBで約2倍のゲインとなっています.このシミュレーション結果からも図4の回路が発振条件を満たしていることが分かります.なお,位相が0度となる周波数とゲインが最大となる周波数が若干ずれています.これは入力抵抗(re)がC1側のみに接続されているためです.
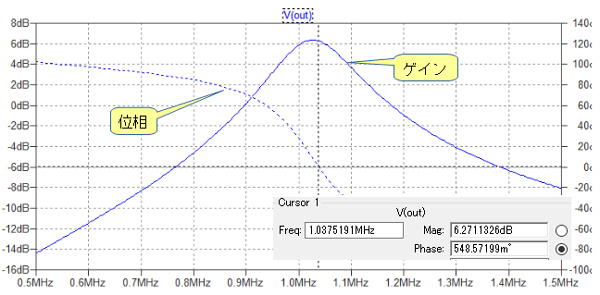
ゲインと位相が発振条件を満たしていることがわかる.
図8が共振回路を図6の右側の共振回路に変更した回路です.図6の右側の共振回路であれば,位相が0度となる周波数とゲインが最大となる周波数は一致します.
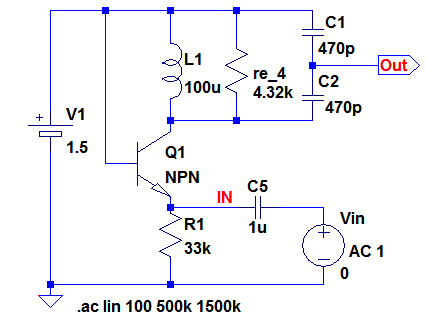
抵抗re_4の値は4*1080=4.32kとしてある.
図9は,図8のシミュレーション結果です.こちらは位相が0度となる周波数とゲインが最大となる周波数が一致しています.このように,図6の左側の回路と右側の回路は,厳密には若干異なった特性となりますが,その誤差は発振条件の概算を行う上では許容範囲内です.
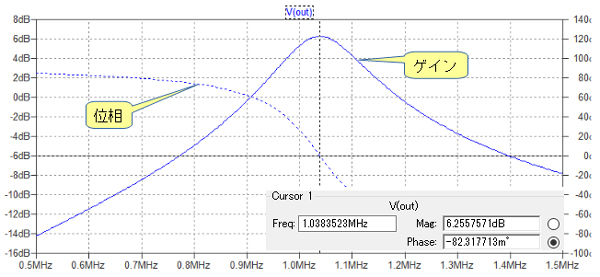
ゲイン最大と位相0度が同じ周波数になっている
図10は,図1のシミュレーション用の回路です.
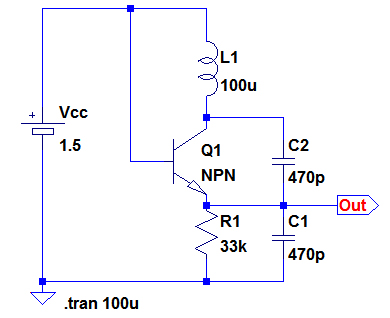
100μsecまでトランジェント解析を行う.
図11は,図10のシミュレーション結果です.上段が出力波形で下段はその出力波形の80μsec~100μsecをFFT解析したものです.40μsecあたりから発振が始まり,その発振周波数は1.037MHzであることが分かります.
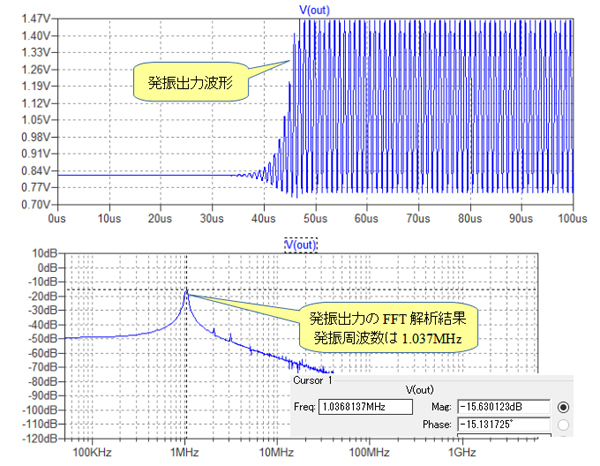
発振周波数は1.037MHzとなっている.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_029.zip
●データ・ファイル内容
Colpitts_Gain1.asc:図5の回路
Colpitts_Gain2.asc:図8の回路
Colpitts.asc:図10の回路
Colpitts2.asc:図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










