ギルバート型乗算回路の出力波形はどれ？
図1は，差動増幅回路が縦積みされたギルバート型乗算回路です．上側の差動回路の入力信号(IN1)は，1kHzで10mVPPの正弦波をV1で発生させています．下側の差動回路の入力信号(IN2)も，上段と同じ1kHzで10mVPPの正弦波をV2で発生させています．
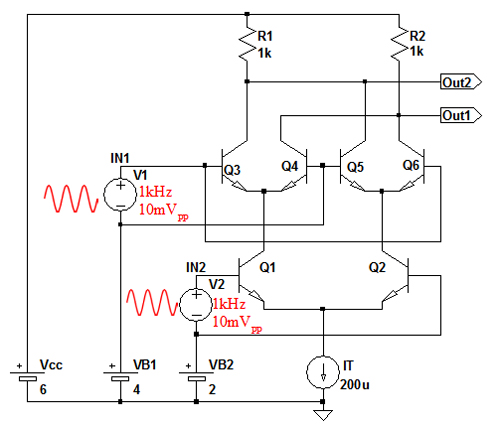
V1とV2共に1kHzで10mVPPの正弦波発生させている．
図2の(A)～(D)は，図1の回路の入出力波形を示しています．上段がOut1端子とOut2端子の差電圧出力で，中段がV1出力，下段がV2出力となっています．そこで，この回路の差動出力電圧の波形として適切なものは図2の(A)～(D)のどれしょうか．
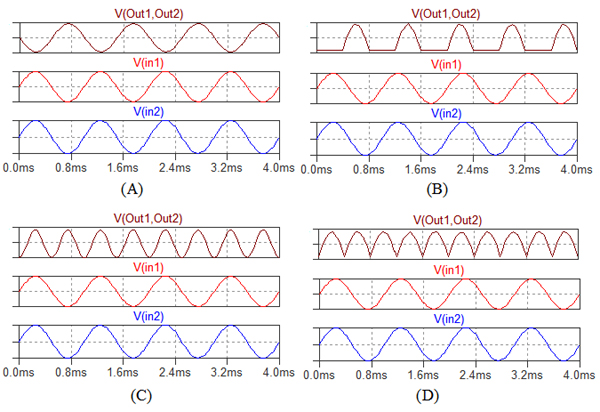
(A)～(D)の中で図1の差動出力電圧の波形として適切なものはどれか？
図1の回路はギルバート型乗算回路と呼ばれ，二つの入力信号の乗算を行うことができる回路です．入力信号が二つとも1kHzで10mVPPの正弦波であることを考えれば，出力波形がどのようになるかがわかります．
図1の回路は，入力信号が10mVPPと小さいので，リニアなV1とV2の乗算回路として働きます．その出力は，上側の差動に入力された信号と，下側の差動に入力された信号を乗算したものになります．
図1のV1とV2は共に1kHzで10mVPPの正弦波です．これを「A×sin(ωt)」とすると出力は二つの信号の乗算なので「A×sin(ωt)×A×sin(ωt)」となります．これに三角関数の公式の「sin(x)×sin(y)=(cos(x-y)+cos(x+y))/2」を適用すると「A×sin(ωt)×A×sin(ωt)=A2×(1-cos(2ωt))/2」となります．これは周波数が2倍の正弦波となることを意味します．出力が入力の2倍の周波数の正弦波となっているのは(C)なので正解は(C)ということになります．
●ギルバート型乗算回路で乗算ができる理由
図1の回路はQ1とQ2からなる差動回路の上にさらに「Q3，Q4」と「Q5，Q6」の差動回路が接続されています．入力電圧とそれぞれのトランジスタのコレクタ電流の関係式から，図1の回路が乗算回路として働く理由を考えてみます．
入力電圧(V2)とQ1とQ2のコレクタ電流IC1とIC2の関係はそれぞれ，式1，式2で表すことができます．
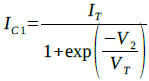・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
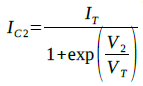・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
Q1のコレクタ電流(IC1)が「Q3，Q4」の差動回路のテール電流となるため，入力電圧(V1)とQ3，Q4のコレクタ電流IC3とIC4の関係はそれぞれ，式3，式4で表すことができます．
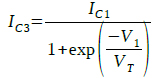・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
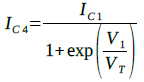・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
同様に，Q2のコレクタ電流(IC2)が「Q5，Q6」の差動回路のテール電流となるため，入力電圧(V1)とQ5，Q6のコレクタ電流IC5とIC6の関係はそれぞれ，式5，式6で表すことができます．
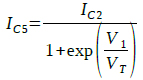・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
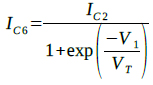・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
負荷抵抗(R1)に流れる電流はQ3とQ5のコレクタ電流を足したもので，負荷抵抗(R2)に流れる電流はQ4とQ6のコレクタ電流を足したものです．そのためOut1端子とOut2端子の差電圧出力(VOUT)は式7で表せます．
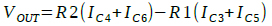・・・・・・・・・・・・・・・・・・・・・・・・(7)
式3のIC1に式1を代入すると，式3は式8のように変形できます．
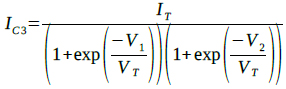・・・・・・・・・・・・・・・・・・・・・・・(8)
同様に式4，5，6は式9，10，11のように変形できます．
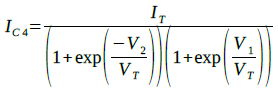・・・・・・・・・・・・・・・・・・・・・・・(9)
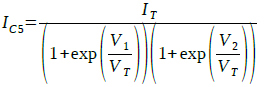・・・・・・・・・・・・・・・・・・・・・・・・(10)
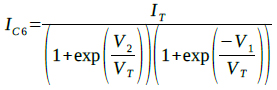・・・・・・・・・・・・・・・・・・・・・・・(11)
ここで「R1=R2=R」とし，式12のハイパボリック・タンジェントの公式を整理するために適用すると，式7は式13のように整理できます．
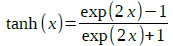・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
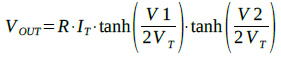・・・・・・・・・・・・・・・・・・・・・・・(13)
さらに，xが1よりも十分小さい領域ではthan(x)≒xと近似できるため，V1，V2が2VTよりも小さい領域では式(13)は式(14)のような近似式で表すことができます．
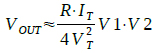・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(14)
以上，長々と計算してきましたが，式(14)からVOUTはV1とV2を掛け合わせたものに比例することになり，図1の回路が乗算回路として働くことがわかります．
●ギルバート型乗算回路のいろいろな使い方
ギルバート型乗算回路は，二つの入力の種類によってさまざまな使い方ができます．ここでは，代表的な次の四つの使い方を紹介し，シミュレーションで確認してみます．
・小振幅の正弦波と小振幅の正弦波
この入力条件では，リニアな乗算回路として動作し，周波数逓倍回路や周波数変換器として使われます．
・小振幅の正弦波と矩形波
この入力条件では，矩形波を入力された差動回路はスイッチング回路として動作し，同期検波回路や平衡変調器として使われます．
・矩形波と矩形波
この入力条件では，すべての差動回路がスイッチング回路として動作し，入力信号の位相差のみを取り出すことができるため，位相検波回路として使われます．
・小振幅の正弦波と直流電圧
この入力条件では，直流電圧によってゲインの変わる可変利得アンプとして使われます．
●小振幅の正弦波と小振幅の正弦波の乗算
図3は，図1と同じ回路で，小振幅の正弦波と小振幅の正弦波が入力の場合で，リニアな乗算回路として動作します．V1とV2はSINE(0 5m 1k)とし，10mVPPの正弦波としています．
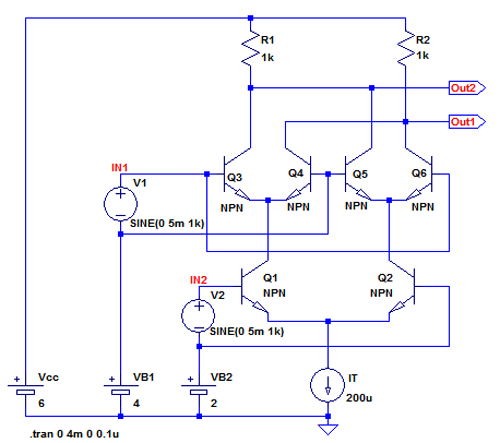
V1，V2はSINE(0 5m 1k)とし，10mVPPの正弦波としている
図4は図3のシミュレーション結果です．上段がOut1端子とOut2端子の差電圧出力です．入力信号の2倍の周波数のきれいな正弦波となっていることがわかります．
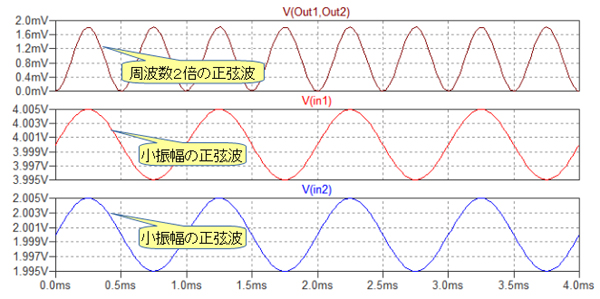
出力信号の周波数は入力信号の2倍となっている
●小振幅の正弦波と矩形波の乗算
図5は，小振幅の正弦波と矩形波の乗算を行う回路で，V1をPULSE(-100m 100m 0 1u 1u 499u 1m)としてV2と同じ周波数で200mVPPの矩形波としています．
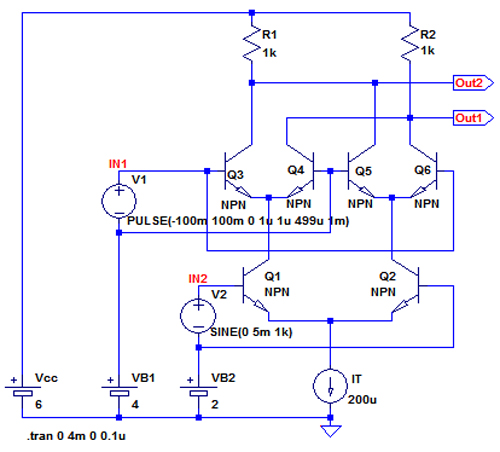
V1はV2と同じ周波数で200mVPPの矩形波となっている
図6がそのシミュレーション結果です．この回路は同期検波回路として働き，V2の正弦波信号を全波整流した出力が得られています．
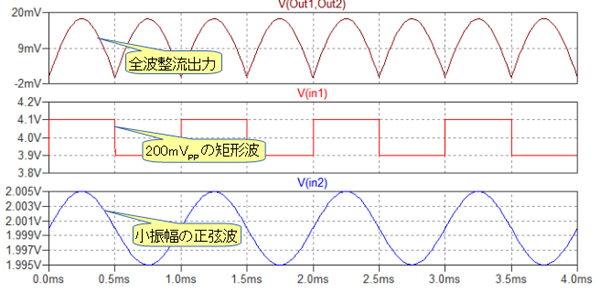
出力はV2の正弦波信号を全波整流したものとなっている
●矩形波と矩形波の乗算
図7は矩形波と矩形波の乗算を行う回路で，V1をPULSE(-100m 100m 0 1u 1u 499u 1m)として1kHzで200mVPPの矩形波とし，V2はPULSE(-100m 100m 100u 1u 1u 499u 1m)として同じ周波数で100μ秒だけ位相のずれた200mVPPの矩形波としています．
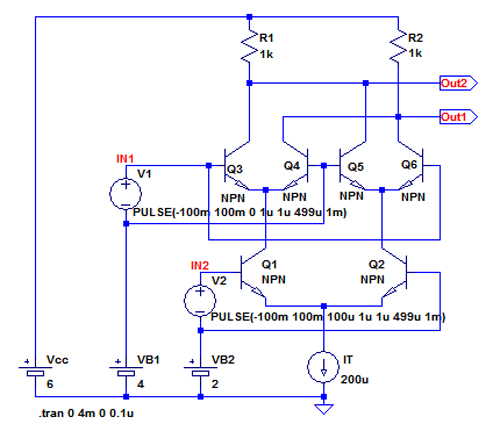
V1とV2は位相のずれた200mVPPの矩形波となっている
図8がそのシミュレーション結果です．この回路は位相検波回路として働き，V1とV2の位相差に比例したパルスが出力されます．
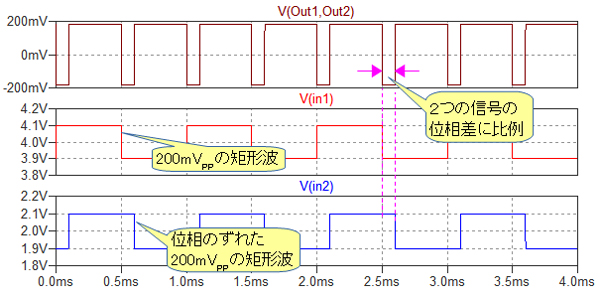
V1とV2の位相差に比例したパルスが出力される
●小振幅の正弦波と直流の乗算
図9は小振幅の正弦波と直流の乗算を行う回路で，V1をPWL(0 -100m 50m 100m)として-100mVから+100mVまで50m秒で変化させ，直流電圧に対する出力の変化のようすをシミュレーションしています．
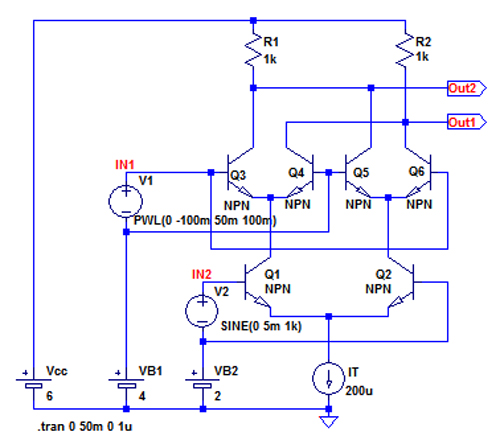
V1は-100mVから+100mVまで変化させている
図10がそのシミュレーション結果です．この回路は可変利得アンプとして働きます．V1が-100mVから0Vに近づくにつれゲインが小さくなり，V1が0Vの時，出力信号は0になります．V1が+側に増加すると再びゲインが増大しますが，V1=0Vを境に出力の位相が反転します．
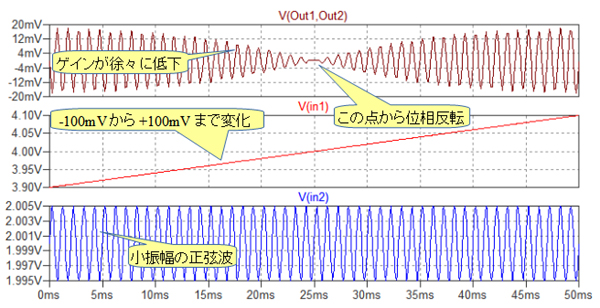
V1の変化によって，出力振幅が変化している
以上，ギルバート型乗算回路の使用例を簡単に紹介しました．この回路の応用範囲は非常に広く，入力ダイナミック・レンジ拡大やMOSトランジスタでの構成などさまざまな改良が行われています．現在も集積回路の主要構成要素として活用されています．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice2_021.zip
●データ・ファイル内容
Gilbert_multiplier_sine_sine.asc：図3の回路
Gilbert_multiplier_Pulse_sine.asc：図5の回路
Gilbert_multiplier_Pulse_Pulse.asc：図7の回路
Gilbert_multiplier_DCSWP_sine.asc：図9の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
