500kHzの進相補償を作るコンデンサ容量値は何pF?

図1はOPアンプ内部の出力抵抗が80ΩのLT1128を使用し,R1を1kΩ,R2を10kΩとした低周波のゲインが20dBの反転増幅器です.反転増幅器の出力には,負荷抵抗(RL)を2kΩ,負荷容量(CL)を100pFが接続されています.C1は負帰還を安定させるために使うコンデンサです.ここで,負帰還の安定性補償において,位相が遅れる周波数をポールと呼び,位相を進ませる周波数をゼロと呼びます.
図2は,図1のC1が無い状態でループ・ゲインと位相特性を調べました.この結果より位相余裕は27°しかありません.さらに位相余裕を増やすため,対策として2ndポールの500kHz付近へ進相補償をするゼロをC1によって作ります.この場合,ゼロが500kHzに最も近いC1の値は,次の(A)~(D)のうちどれでしょうか?
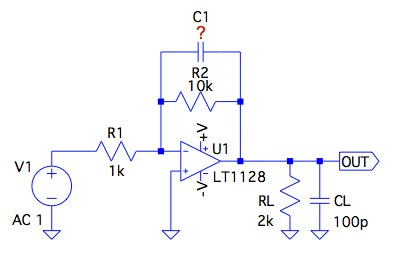
出力に負荷抵抗(RL)を2kΩ,負荷容量(CL)を100pFが接続され,ゲインは20dB.
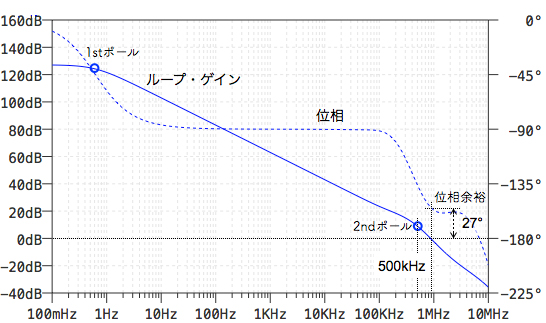
位相余裕が27°しかない.
図1の負帰還ループが閉じた状態をクローズ・ループと呼び,この場合のC1はロー・パス・フィルタのように高周波のゲインを小さくします.一方,負帰還ループを一巡するループ・ゲインと位相で考えると,C1はハイパス・フィルタのように高周波でループ・ゲインを大きくし,位相を進ませる働きがあります.
図1において進相補償のゼロをfzとします.fzはR1,R2,C1からなる帰還率β(s)で作ることができ,図1のゼロは「fz=1/2πC1R2」となります.「R2=10kΩ」ですので,問題の(A)~(D)の条件についてfzを調べると次のようになります.
(B)C1=22pF fz=723kHz
(C)C1=33pF fz=482kHz
(D)C1=47pF fz=339kHz
したがって,500kHzに最も近いゼロは,fz=482kHzであり,(C)の33pFです.
●負帰還の安定性評価はループ・ゲインと位相特性を使う
OPアンプを使った負帰還回路は,不安定になると出力が発振します.マイクとスピーカーを近づけるとハウリングが発生し「キーン」という音が聞こえるのと同じで,正帰還ループになるためです.ここでは,図1の反転増幅器の負帰還安定性について,負帰還を一巡するループ・ゲインと位相特性を用いて,正帰還にならないように位相をコントロールする補償をし,また補償後の効果について説明していきます.
負帰還の安定性は,回路のループを一巡するループ・ゲインと位相特性を用いて評価します.図3は,負帰還回路を一巡するループをOPアンプのオープン・ループ・ゲインA(s)と帰還率β(s)をブロック図で示しました.また,負帰還ループをOPアンプの反転端子で切り離して「va」,「vc」として,OPアンプ内部の-A(s)vaのオープン・ループ・ゲインを持った電圧源とROの接続点を「vb」とします.
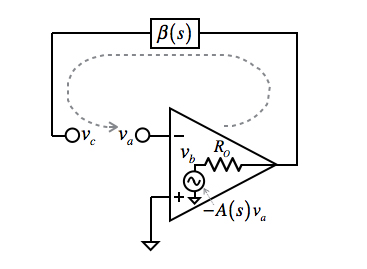
ループ・ゲインはva~vcを一巡する特性.
図3で負帰還が不安定になり発振するメカニズムを説明するとvaからvbを通りvcに至るまでの経路で位相が360°遅れ正帰還になるためです.位相が360°遅れる原因は次の三つとなります.
2.同様にvaからvbの経路で,OPアンプの高周波帯での周波数特性により更に位相が遅れます
3.vbからvcの経路につく容量でも位相が遅れます
図2の位相特性は,C1が無く,出力にRL,CLが付いた状態でvaからvcまでのループ・ゲインと位相を示したものです.位相余裕が27°ということは,vaから入力し,vcで同じ振幅値(0dB)となる条件において,位相の遅れが正帰還になるまで27°しか余裕がない状態です.
●進相補償のゼロは負帰還の抵抗とコンデンサで作る
図4は,図3の帰還率β(s)を図1のR1,R2,C1,RL,CLで表した回路です.帰還率β(s)なのでvbを入力として,vcを出力とすると,帰還率β(s)はC1により高周波でゲインが大きくなり位相が進むハイパス・フィルタと同じ役割です.この位相が進み始める周波数を,図2の位相が遅れる2ndポールの周波数(500kHz)へあわせることにより補償します.
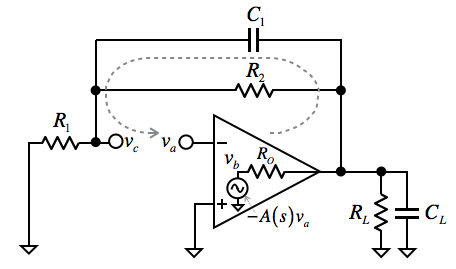
帰還率β(s)はvb~vcを一巡する特性.
図4のvbからvcまでの帰還率β(s)を計算すると式1となります.
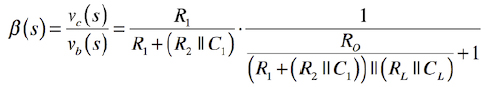 ・・・・・・・・・・(1)
・・・・・・・・・・(1)
ここで式1は複雑ですので,図1のゼロ周波数(500kHz)でのC1とCLのインピーダンスを求め,式1に代入して近似式を求めます.500kHzでのC1のインピーダンスをZC1,また,CLのインピーダンスをZCLとするとC1が33pFのインピーダンス(ZC1)は「1/(2π*500kHz*33pF」で9646Ωとなります.同様の計算でCLが100pFのインピーダンス(ZCL)は3183Ωとなります.また,図1のOPアンプ内部の出力抵抗(RO)は80Ωで,R1が1kΩ,R2が10kΩ,RLが2kΩです.これらの値を代入した式が式2です.
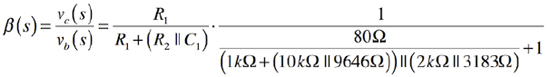 ・・・・・(2)
・・・・・(2)
さらに整理した式が式3となります.
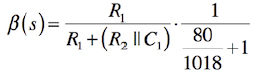 ・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3の右辺の「80/1018」は十分小さいため,近似式は式4となります.
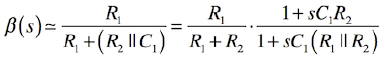 ・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・(4)
帰還率β(s)の位相を進ませるゼロの周波数は式4の分子なので,その周波数(fz)は式5となります.このときの帰還率β(s)のゲインは,1次ハイパス・フィルタと同じですので,低周波でのゲインから+3dBが見込めます.
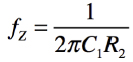 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
また,式4の分母は,新たに位相遅れするポールがあることを示しており,その周波数fpは式6となります.式6より,新たに生まれるポールの周波数は,ゼロの周波数より「(R1+R2)/R1」から11倍高い周波数ですので,ゼロの500kHz付近への影響は少ないです.
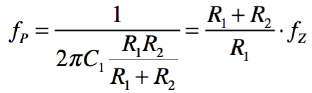 ・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・(6)
次に式5で求めた帰還率β(s)のゼロを,図5の図1の帰還率β(s)の等価回路を用いてLTspiceで確認します.図5のvbとvcは図4のvbとvcに対応します.C1の容量値は変数とし,問題の(A)~(D)の条件の他にC1が0pFの状態も参考のため入れました.
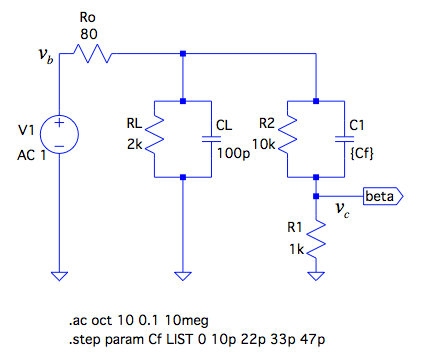
図5のvbとvcは図4のvbとvcに対応.
図6は,図5のシミュレーション結果となります.図6において,C1が0pFのときは,位相を進ませるゼロがなく,C1があることにより補償のゼロが作られていることが分かります.帰還率β(s)は高周波でゲインが上がり,位相も進んでいます.解答のC1が33pFを調べると,ゼロの周波数(fz=482kHz)で帰還率β(s)のゲインは,低周波のゲインから約+3dBであり,式4で作成したゼロと同じであることが確認できます.
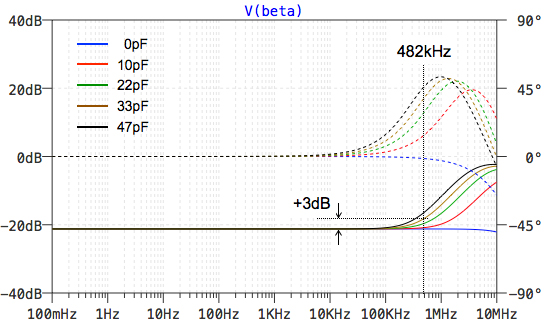
C1が0pFのときは,位相を進ませるゼロがなく,C1があることにより補償のゼロが作られていることが分かる.
●ループ・ゲインと位相のシミュレーション
ここまで帰還率β(s)で負帰還を安定させるゼロを作成しました.次に図1の回路が安定か否かを判別するループ・ゲインと位相のシミュレーションをおこないます.図4では説明のため反転端子でループを切断しましたが,OPアンプにはオフセット電圧やオフセット電流,入力バイアス電流などがあるため,図4のように回路図上で切断すると,OPアンプのオープン・ループ・ゲインが非常に大きいことから,出力が飽和してしまいます.この問題を回避し,ループ・ゲインと位相を調べる方法としてMiddlebrook法を用います.
図7は,図1のループ・ゲインと位相についてMiddlebrook法を用いて調べる回路です.二つの同じ回路を用意し破線で囲んだ理想素子を回路へ加えることによって,図7上段にある計算式にてループ・ゲインと位相特性が調べられます.ここでC1は,帰還率β(s)のシミュレーションと同様に変数とし,値を変化させました.
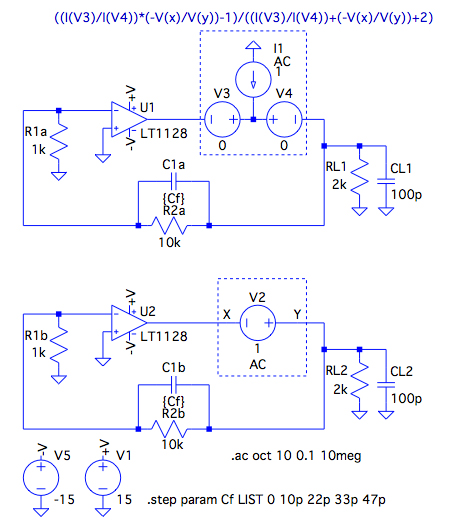
ループ・ゲインと位相について調べる.
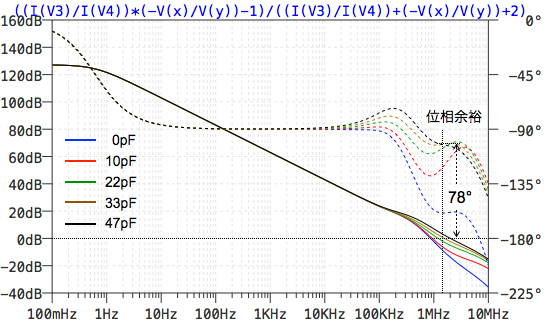
図8は,図7のシミュレーション結果です.C1により帰還率β(s)にゼロができるため,ループ・ゲインと位相も変化し,C1が33pFの場合は,位相余裕が78°まで増加していることが分かります.
Middlebrook法については,LTspiceのインストールディレクトリのEducationalフォルダに「LoopGain.asc」のファイル名でコメント付きの回路図がありますので,そちらも参考にしてください.Windows7の環境では,「C:\Program Files (x86)\LTC\LTspiceIV\examples\Educational」です.動画1では,LTspiceのMiddlebrook法の動作を解説しています.
●ゼロで補償した反転増幅器のシミュレーション
最後にゼロで補償した反転増幅器のゲイン周波数特性と時間応答のシミュレーションでその効果を調べます.図9は,図1の周波数特性を調べる回路で,C1を変数として変化させます.
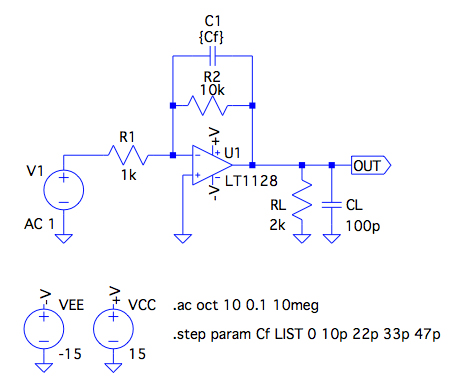
C1を変数として変化させる.
図10がその結果です.この回路のゲインは「C1とR2の合成インピーダンス÷R1」で求められます.低周波では,C1のインピーダンスが大きいため「R2/R1」の抵抗比であり,周波数が高くなるとC1のインピーダンスが小さくなるためゲインは下がります.これをゲイン伝達関数で示すと式7になります.
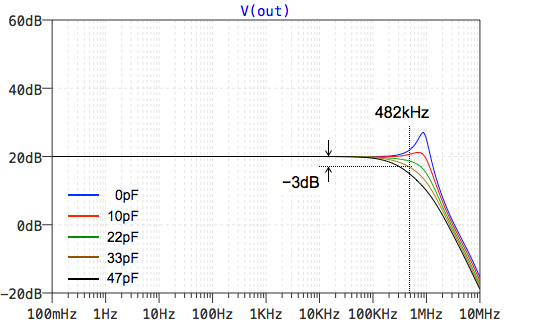
C1が33pFのシミュレーション結果で-3dBとなるカットオフ周波数が482kHzであることが分かる.
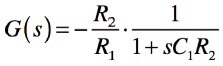 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7は,低周波のゲインは「R2/R1」で,カットオフ周波数「1/2πC1R2」の1次ロー・パス・フィルタの特性を示しており,ゲインが下がり始めるカットオフ周波数は式5と同じになります.図10のC1が33pFのシミュレーション結果でも低周波のゲインは「R2/R1=10(20dB)」で,-3dBとなるカットオフ周波数が482kHzであることが分かります.
図11は,図1の時間応答を調べる回路です.具体的には立上がりと立下がり時間が0.1μsの矩形波を入力し,出力の時間応答を調べます.C1は前述と同じように変数で値を変化させます.
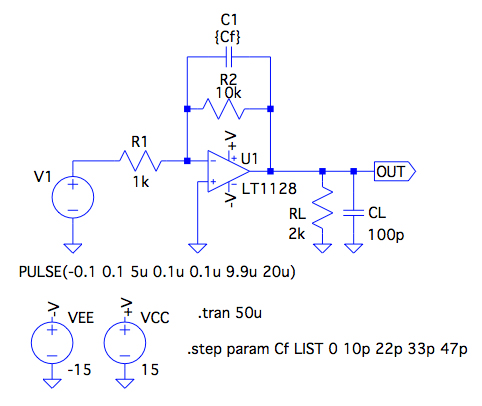
立上がりと立下がり時間が0.1μsの矩形波を入力し,出力の時間応答を調べえる.
図12がシミュレーション結果です.図12のC1が0pFでは出力の立上がり,立下がりでリンギングしており,発振の予兆がみえます.C1の値が大きくなると,リンギングは小さくなりゼロによる補償の効果が分かります.
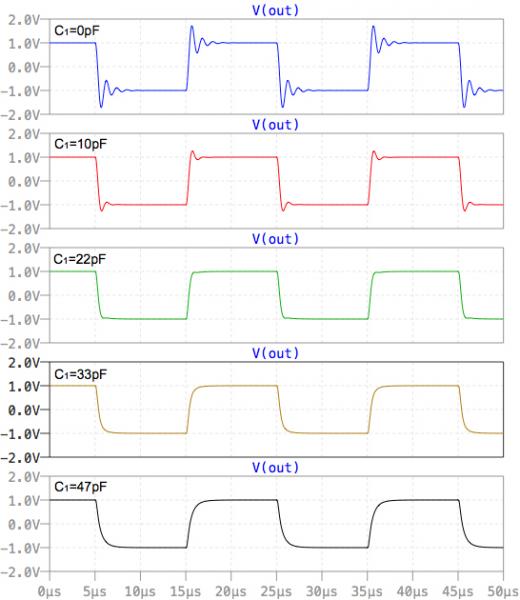
C1が0pFでは出力の立上がり,立下がりでリンギングしており,発振の予兆がみえる.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_012.zip
●データ・ファイル内容
LoopGain.asc:図7の回路
CloseLoop_ac.asc:図9の回路
CloseLoop_tran.asc:図11の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










