出力が大振幅の場合,波形がひずむ入力振幅は何V?

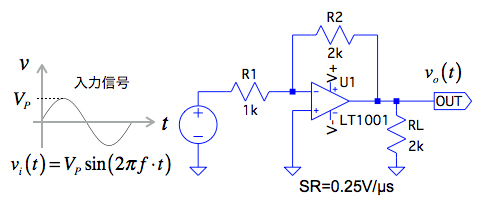
図1は,図2の最大出力応答周波数(最大無ひずみ出力と周波数)を持つOPアンプ(LT1001)を用いた反転増幅器です.最大出力応答周波数は,OPアンプのスルー・レート(SR)と関係があり,LT1001のSRは0.25V/μsです.回路定数は,OPアンプの電源を±15V,R1を1kΩ,R2を2kΩ,負荷抵抗(RL)を2kΩとして,周波数が10kHzの正弦波を入力へ印加します.この入力振幅(VP)の振幅値を0.5V,1V,2V,3Vと変更した場合,出力の波形がひずむ入力振幅値は次の何Vでしょうか.
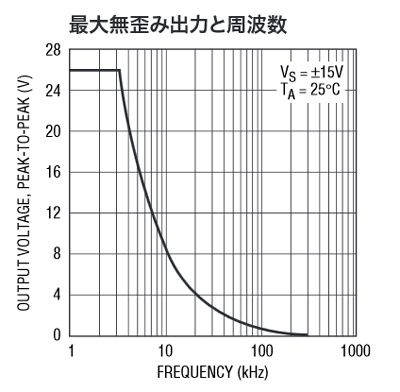
OPアンプを使った増幅器は,出力が大振幅のときの時間応答は,スルー・レートで制限されます.その関係を示した,最大出力応答周波数特性が,図2の「最大無ひずみ出力と周波数(Maximum Undistorted Output vs. Frequency)」です.
スルー・レートは,OPアンプの出力が「1μsあたり何V変化できるか」を示す規格で,単位は[V/μs]です.LT1001のスルー・レートは,その電気的特性の標準値で0.25V/μsですので,1μsあたり最大で0.25V変化できることになります.
図1の反転増幅器の出力電圧が大振幅時の周波数特性は,図2の「最大無ひずみ出力と周波数」で示されます.ここでは,この特性を最大出力応答周波数特性と呼ぶことにします.
図2の最大出力応答周波数は,出力が入力に追随する最大振幅の周波数特性を示しており,横軸が周波数,縦軸が出力波形の最大値‐最小値間(ピーク・ツー・ピーク値)の電圧です.問題の入力信号周波数は10kHzですので,図2より,増幅器の出力が入力に追随できる最大振幅が,ピーク・ツー・ピーク(P-P)値で8VP-Pであることが分かります.
図1の反転増幅器で,入力の正弦波信号の振幅(VP)が0.5V,1V,2V,3Vのとき,増幅された出力信号のP-P値の電圧を計算し,先ほど図2から求めた出力が入力に追随できる最大振幅8VP-P以内か,またはそうでないかを調べます.
入力信号の正弦波は,図1に記載している「vi(t)=VP*sin(2πf*t)」であり,振幅(VP)は,正弦波振幅の中心から正負に振れる片側の振幅値です.入力信号は正負に振れていることから,P-P値に直すと2倍になります.これよりVPが0.5V,1V,2V,3VのときP-P値に換算すると,それぞれ1V,2V,4V,6Vとなります.
図1の反転増幅器のゲイン(G)は「G=-1*(R2/R1)=-2」より,出力が反転した2倍のゲインなので,入力振幅がP-P値換算の1V,2V,4V,6Vを2倍のゲインで増幅すると,出力振幅のP-P値はそれぞれ2V,4V,8V,12Vになります.
図2より,周波数10kHzで出力が入力に追随できる最大振幅は8VP-Pなので,反転増幅器の出力が2VP-P,4VP-P,8VP-Pとなる振幅(VP) 0.5V,1V,2Vは,出力は入力に追随できることから波形がひずみません.一方,出力が12Vとなる振幅(VP) 3Vは,出力は入力に追随できず,出力波形がひずみます.ゆえに,解答は(D)の3Vとなります.
●最大出力応答周波数特性とスルー・レートの関係
図3は,図1と同じゲインが2倍の反転増幅器で,OPアンプのスルー・レートの違いによる最大出力応答周波数の具体的な波形二つと入力を示しています.OPアンプの違いは,スルー・レート(0.25V/μs)が小さいLT1001と,スルー・レートが大きい(無限大)理想OPアンプとなります.また,入力は問題よりも大きな4Vの振幅(8VP-P)で,周波数は10kHzです.
図3のスルー・レートが大きい理想OPアンプの場合,出力は入力に対し,反転した波形で追随し,出力波形のひずみはありません.一方,スルー・レートが小さいLT1001の出力は入力に追随できず,出力波形は三角波になります.この場合,出力振幅を小さくし,出力が入力に追随できる最大出力応答周波数特性に合わせる必要があります.LT1001の場合,図2より10kHzでは,出力振幅を8VP-P以内にします.このように最大出力応答周波数は,OPアンプのスルー・レートと強い相関があります.
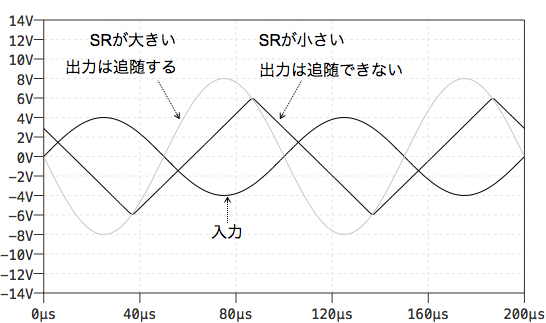
スルー・レートが小さいと出力は入力に追随できない
●スルー・レートとフルパワー・バンド幅の関係
スルー・レートは,出力の最大変化率を示すもので,具体的には矩形波を入力し,増幅器出力の時間応答から測定します.図4は,反転増幅器の出力波形例です.スルー・レートは,出力電圧の10%から90%に至る振幅をそれに要する時間で除算した傾きとなります.図3のスルー・レートが小さい出力波形は,入力に追随できずに三角波になっていますが,これは,図4のスルー・レートの同じ傾き(0.25V/μs)が出ています.
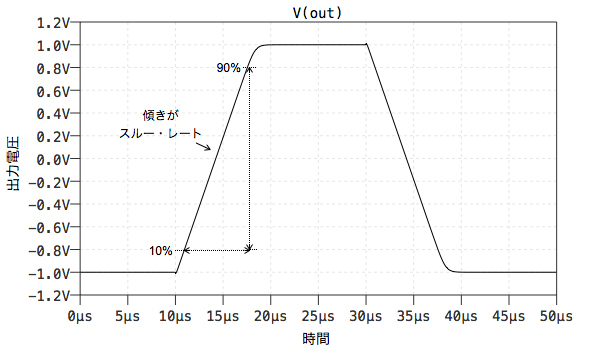
ここで, 出力における正弦波の最大変化率を調べ,スルー・レートとの関係を導きます.式1は,増幅器出力の正弦波を示す式です.
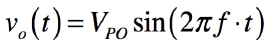 ・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・(1)
正弦波の最大変化率は式1を時間で微分することにより求められ,式2となります.
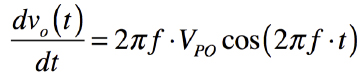 ・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・(2)
式2の中のコサインの最大値は「1」です.また,出力を時間で微分した傾はスルー・レートなので,スルー・レート(SR)と周波数(f)と出力振幅(VPO)には式3の関係となります.
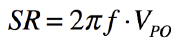 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
ここで式3を変形すると式4になります.
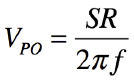 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式4を用いて,図1の条件と同じ,OPアンプのスルー・レートを0.25V/μs,周波数を10kHzとして,最大振幅を求めると,「VPO=0.25V/μs/2π*10kHz=4V」です.4VをP-P値へ換算すると8VP-Pで,図2のグラフから求まる値と同じになります.
また,式3のfをフルパワー・バンド幅(FPBW)と考えれば,式5のように表せます.
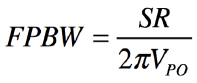 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
このように,図2が無くても,式3の三つのパラメータ(スルー・レート,周波数,出力振幅)のうち二つが分かれば,出力が入力に追随するための関係を導くことができます.
●LTspiceで出力波形を確認する
図5は,図1の回路で問題と同じように,OPアンプの電源を±15V,R1を1kΩ,R2を2kΩ,負荷抵抗(RL)を2kΩとし,入力に周波数が10kHzの正弦波を印加して, 反転増幅器の時間応答を調べる回路です.入力の信号源V1の振幅はVPという変数にして,「.stepコマンド」で0.5V,1V,2V,3Vを与え,4回のシミュレーションを実行します.
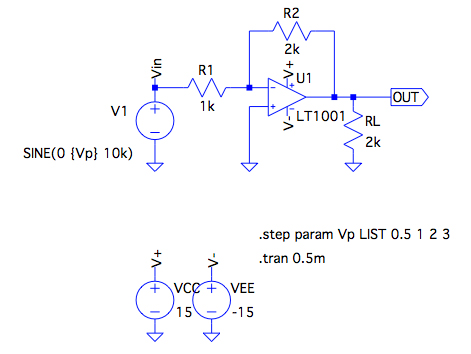
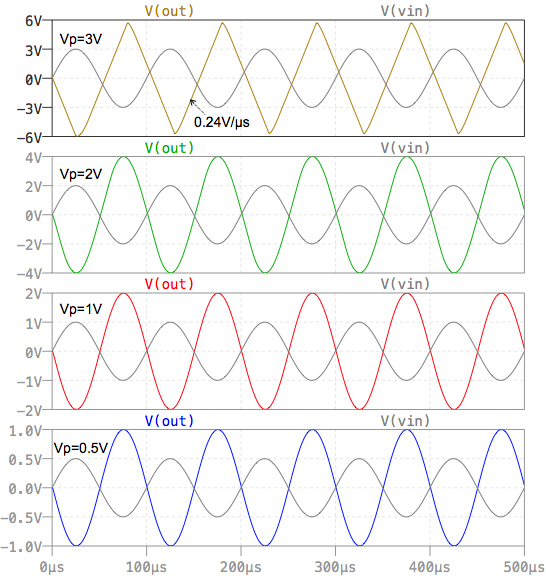
図6がそのシミュレーション結果です.0.5V,1V,2V,3Vの入力振幅ごとに色分けして,出力の時間応答をプロットしています.ここで灰色は入力信号を示しています.
図6のシミュレーション結果も振幅(VP)が0.5V,1V,2Vのときは,出力振幅(VPO)が2V,4V,8Vで正弦波です.振幅(VP)が3Vで,出力振幅(VPO)が12Vの時,出力電圧は三角波になり,スルー・レートの制限を受けていることがわかります.また,そのときの三角波の傾きは0.24V/μsで,スルー・レートに近い値となっています.
以上のように,出力が大振幅の場合,出力が入力に追随し波形のひずみを起こさないようにする値は,図2の最大出力応答周波数特性や式4,式5を用いて求められます.図2のグラフは,半導体メーカーによって呼び名が違う場合がありますので,大振幅の出力信号を扱う場合,最大出力応答周波数特性に注意しましょう.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_008.zip
●データ・ファイル内容
Inverting_Amplifier_Tran_LargeSignal.asc:図5の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










