抵抗比のゲインが正しく出力されない抵抗値は何Ω?

図1は,図2のオープン・ループ・ゲインの周波数特性を持つOPアンプ(LT1001)を用いた反転増幅器です.回路定数は,OPアンプの電源を±15V,R1を100Ω,負荷抵抗のRLを2kΩとして,入力に振幅が1mVで周波数が2kHzの正弦波を印加します.この反転増幅器のR2の抵抗値を100Ω,1kΩ,10kΩ,100kΩと変更した場合,R2/R1の抵抗比のゲインで正しく出力されない抵抗値は次の何Ωでしょうか.
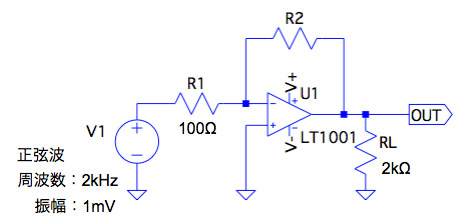
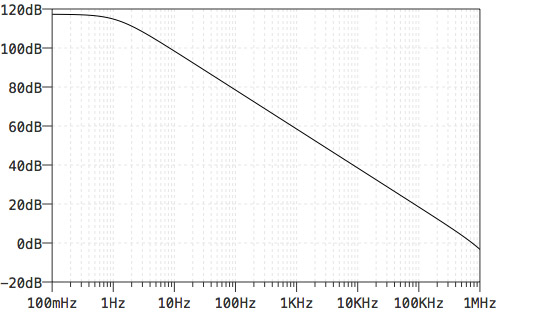
この回路の直流ゲインは,R1とR2の抵抗比「-1×(R2/R1)」で計算できます.「-1」は,反転増幅器出力の位相が180°(入力に対して反転)変わることを意味しています.また,抵抗比で設定する反転増幅器のゲインは,OPアンプのオープン・ループ・ゲインの周波数特性で制限される周波数帯があります.
図1の反転増幅器の周波数特性は,図2のOPアンプのオープン・ループ・ゲインの周波数特性と抵抗比のゲイン[dB]を用いて,難しい計算をしなくても簡単に予測できます.具体的な予測方法を図3に示します.図3は,図2に抵抗比の値や周波数特性を色分けしてプロットした図となります.
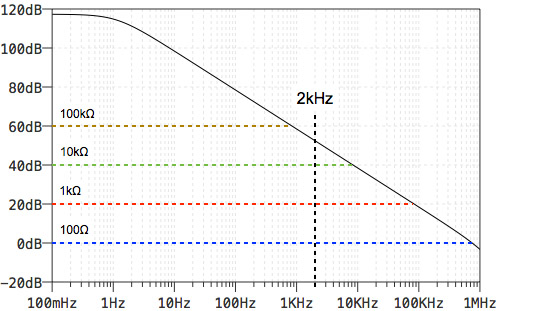
図2へ図1の抵抗比(R2/R1)で求まる周波数特性を色分けしてプロットした.
抵抗比のゲインは,周波数特性を持たないデシベルで表しますので,「-1×(R2/R1)」は,「20×log10(R2/R1)」で計算します.「20×log10(R2/R1)」にR1の値(100Ω)とR2の値(100Ω,1kΩ,10kΩ,100kΩ)を代入すると抵抗比のゲインは,100Ωが「0dB」,1kΩが「20dB」,10kΩが「40dB」,100kΩが「60dB」となります.
次に,デシベルで示した抵抗比のゲイン(0dB,20dB,40dB,60dB)を低周波(ここでは100mHz)の縦軸にプロットします.そのプロットした抵抗比のゲインからオペアンプのオープン・ループ・ゲインと交差するまで横に直線を記入します.抵抗比のゲイン別にできた,直線とオープン・ループ・ゲインの減衰カーブがR2の値を変更した反転増幅器の周波数特性の予測となります.
解答を導くため,問題にある入力周波数2kHzの目盛に縦に線を引きます.100Ω,1kΩ,10kΩは,抵抗比で設定したゲインが見込めます.しかし,100kΩは抵抗比のゲインから外れ,OPアンプのオープン・ループ・ゲインに制限される領域であり,ゲインが下がります.ゆえに,解答は(D)100kΩとなります.
●反転増幅器のゲインは二つの抵抗の比で設定
図4に示す反転増幅器は,OPアンプを使った基本的な増幅器の一つです.この増幅器の出力voは,入力viの極性を反転したものであることから反転増幅器と呼ばれています.
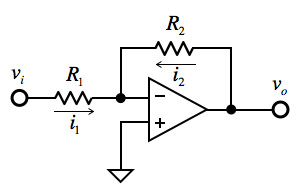
反転増幅器のゲインは,OPアンプを理想とし,また,負帰還があることから,次の二つの規則を用いて求められます.
規則1 OPアンプの二つの入力端子は電流が流れない
規則2 反転端子と非反転端子の電位差はゼロである
OPアンプの非反転端子(+端子)は,図4のようにグラウンドなので,規則2より反転端子(-端子)は「バーチャール・グラウンド」と呼ばれます.図4を用いて規則1,規則2を使い反転増幅器のゲインを計算すると,ゲインは二つの抵抗の比(R2/R1)で,極性が反転されることが分かります.
規則1より,R1に流れる電流は,R2に流れる電流と同じとなり, 式1となります.
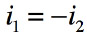 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
規則2より,反転端子はバーチャル・グラウンドなので,R1とR2に流れる電流は式2,式3となります.
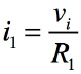 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
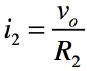 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式1に式2,式3を代入して式を整理すると,ゲインは式4となります.
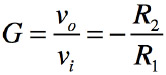 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
このように反転増幅器のゲインは,二つの抵抗の比(R2/R1)で設定でき,出力の極性は入力の反転となるためマイナス(-)が付きます.
●OPアンプのオープン・ループ・ゲインを考慮した反転増幅器
次に,問題のようにOPアンプのオープン・ループ・ゲインが有限で周波数特性をもつ場合を考えます.図5は,OPアンプが理想ではなくオープン・ループ・ゲインをA(s)で表しました.ここで,周波数領域の関数に変換する式は「s=jω」です.
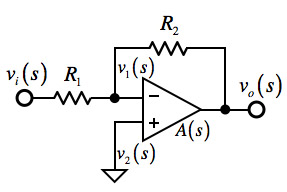
反転端子の電圧をv1(s),非反転端子の電圧をv2(s)とすれば,式5となります.
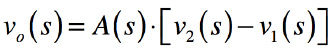 ・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・(5)
規則1より,R1,R2に流れる電流が等しいので,式6となります.
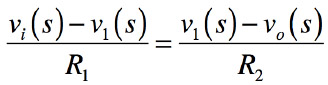 ・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・(6)
v2(s)は,グラウンドでありv2(s)=0,また式6へ式5を代入し整理すると,図5のゲインは,式7となります.
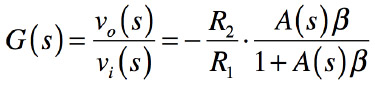 ・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・(7)
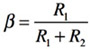 となります.
となります.
式7のA(s)βはループ・ゲインと呼びます.低周波のオープン・ループ・ゲインA(s)は大きく,したがって,ループ・ゲイン[A(s)β]が1より十分大きい「1<<A(s)β」のであれば,反転増幅器のゲインは,抵抗比(R2/R1)で近似できます.これが図3で予測した,抵抗比のゲイン(R2/R1)の横線にあたります.一方,高周波になるほどオープン・ループ・ゲインは小さくなり,ループ・ゲイン「1<<A(s)β」が成り立たなくなると反転増幅器のゲインは小さくなり,OPアンプ自体の周波数特性のゲインとなります.図3では,横線とオープン・ループ・ゲインが交差した点より高周波側がそれにあたります.
OPアンプのオープン・ループ・ゲインの周波数特性は,データシートに図2のようなグラフが記載されています.その図に図3のように作図すれば,反転増幅器のゲインが抵抗比で増幅する周波数領域か,否かが簡単に分かります.
●LTspiceで反転増幅器のゲインの周波数特性を確認する
図6は,図1のR2の値(100Ω,1kΩ,10kΩ,100kΩ)を変化させて,反転増幅器のゲインの周波数特性を調べる回路です.R2の値は{Rf}とし,Rfという名の変数としています.Rfは「.step」コマンドで,抵抗値100Ω,1kΩ,10kΩ,100kΩを与え,4回シミュレーションを行います.
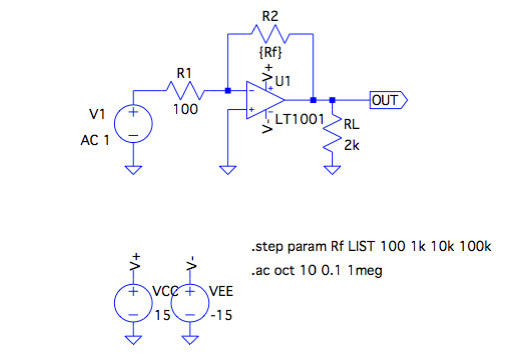
R2の抵抗値を変えて,反転増幅器のゲインの周波数特性を調べる.
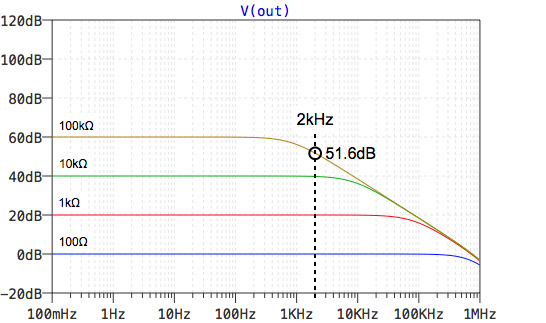
図7がそのシミュレーション結果です.図3で示した直線と同じように,抵抗比(R2/R1)のゲインが,低周波数領域で横一直線となり,高周波数領域でOPアンプのオープン・ループ・ゲインの周波数特性が現れています.図3のR2/R1の横一直線とオープン・ループ・ゲインが交差するあたりは,式7のオープン・ループ・ゲイン「A(s)」が徐々に変わるため,図7では滑らかにゲインが下がります.周波数2kHzのときのゲインをカーソルで調べると,100Ω,1kΩ,10kΩはR2/R1のゲインですが,100kΩのときは約51.6dB(380倍)であり,R2/R1のゲインではありません.
次に同じ回路を過渡解析で調べます.図8が過渡解析の回路で,図1と同様に,R2の抵抗値(100Ω,1kΩ,10kΩ,100kΩ)を変化させて,振幅が1mVで周波数が2kHzの正弦波を印加し,時間軸での応答を調べます.
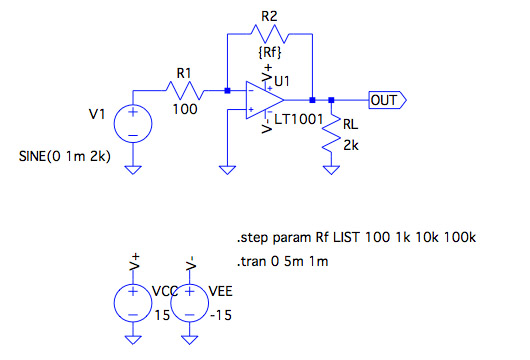
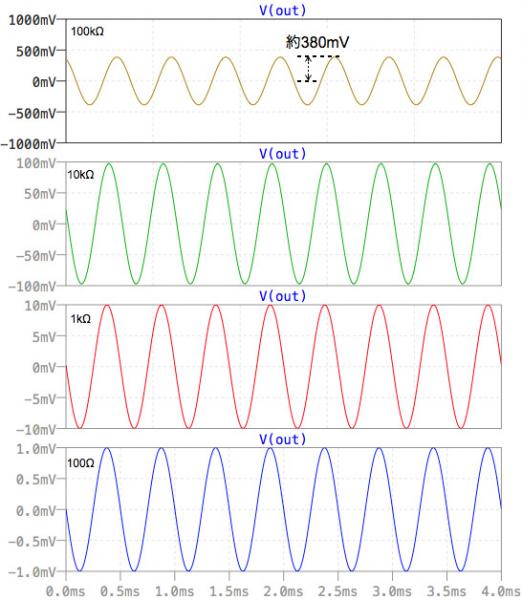
R2の抵抗値を変えて,時間軸での応答を調べる.
図9がそのシミュレーション結果です.四つの抵抗値ごとにプロットしています.縦軸の上限と下限はR2/R1のゲインで得られる出力電圧値としており,正弦波がフルスケールで振れていればR2/R1のゲインであることが一目でわかるようにしています.図9の過渡解析の結果でも100Ω,1kΩ,10kΩはR2/R1のゲインですが,100kΩのときは約380mVであり,図7の結果から得られた51.6dBであることがわかります.
最後に,問題のLT1001のような汎用OPアンプは電圧帰還型OPアンプと呼びます.電圧帰還型OPアンプは図7のシミュレーション結果のように,抵抗比で決まるゲインを大きくすると,帯域が狭くなる欠点があります.交流信号を増幅するときは注意しましょう.また,ゲインの計算で使用した規則1,規則2は,負帰還のOPアンプの回路計算でよく使用します.これらの規則を使うと回路の計算が楽になります.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_006.zip
●データ・ファイル内容
Inverting_Amplifier_AC.asc:図6の回路
Inverting_Amplifier_Tran.asc:図8の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










