トランジスタの相互コンダクタンスが10mSになるコレクタ電流は?

図1左は,トランジスタのベース・エミッタ間電圧(VBE)とコレクタ電流の関係をシミュレーションするための回路です.図1右は,図1左の結果となります.トランジスタを使って増幅回路を設計するときの重要なパラメータに相互コンダクタンス(gm)があります.図1のようにトランジスタのベースに直流電圧を加え,そこに微小電圧変化を与えたときのコレクタ電流(IC)の微小変化の割合が相互コンダクタンスです.図1左のトランジスタで相互コンダクタンスが10mSになるコレクタ電流の値は次の(A)~(D)のどれでしょうか.
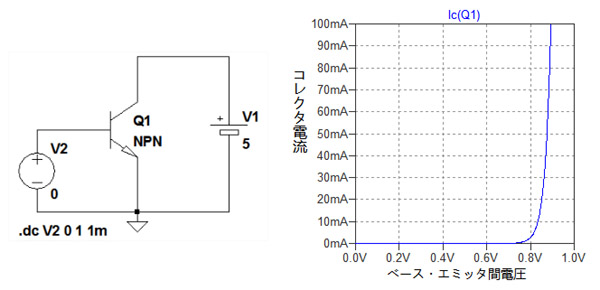
このトランジスタで相互コンダクタンスが10mSになるコレクタ電流の値はいくつか?
1Sは1mVの電圧変化に対して1mAの電流変化があることを表しています.図1右のグラフの曲線の傾きは,ベース・エミッタ間電圧(VBE)及びコレクタ電流(IC)によって変わります.この曲線の傾き(ΔIC/ΔVBE)が相互コンダクタンス(gm)です.
相互コンダクタンスの単位にはS(siemens:ジーメンス,シーメンスとも読まれる)を使用します.ドイツ人学者Ernst Werner von Siemens(エルンスト・ヴェルナー・フォン・ジーメンス)の名前に由来しています.また,コンダクタンス(G)は,電流の流れやすさを表し抵抗の逆数で,単位はSを使用します.
図1右のグラフから相互コンダクタンスとコレクタ電流の関係を読み取るのは大変でが,エミッタ接地トランジスタの相互コンダクタンス(gm)とコレクタ電流(IC)の関係はどんなトランジスタでも式1で表すことができます.
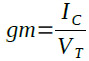 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
そこで,この式を使って(A)~(D)の相互コンダクタンスを求めてみます.ここでVTは熱電圧と呼ばれ,常温(27℃)で値が26mVとなります.式1に(A)~(D)のコレクタ電流値とVT値を代入すると,それぞれの相互コンダクタンスは,(A)が385μS,(B)が10mS,(C)が32.3mS,(D)が385mSとなります.相互コンダクタンスが10mSになるのは(B)ですから,正解は(B)ということになります.
●増幅回路の設計で相互コンダクタンスは重要
図1の相互コンダクタンスの値の検討をする前に,なぜ増幅回路の設計で相互コンダクタンスが重要なのかを簡単に説明します.一般的な増幅回路は小さな入力電圧を大きな出力電圧に変換する働きをします.その増幅素子としては,図2のように,入力された電圧に対して一定の割合で電流を出力するものが使用されます.その出力電流が負荷抵抗で再度電圧に変換され,出力になります.この素子の入力電圧を出力電流に変換する係数が相互コンダクタンス(gm)です.図2の回路で出力電圧(VOUT)は「IOUT*RL」で表されます.またIOUTは「gm*Vin」ですから,まとめるとVOUTは式2になります.
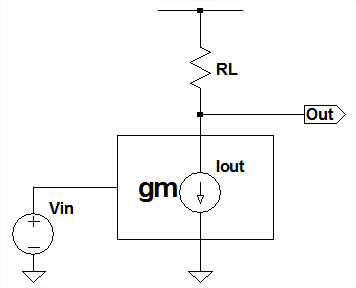
相互コンダクタンス(gm)を使うとゲインが簡単に計算できる.
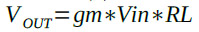 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
ゲイン(G)は,VOUTをVinで割ったものなので,式3で表すことができます.
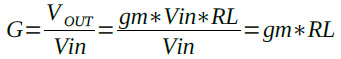 ・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・(3)
式3を使用することで,相互コンダクタンスがわかれば簡単にゲイン(G)を求めることができます.たとえば,RLが1kΩで相互コンダクタンスが10mSであれば,「G=1k*10m=10」と10倍のゲインになります.また,負荷抵抗とゲインが決まっている場合,相互コンダクタンスをいくつにすれば良いのか求めることができます.このように相互コンダクタンスを使うと増幅回路のゲイン設計を簡単に行うことができる非常に有用なパラメータです.
●VBEとICの関係からgmを求める
ここから,トランジスタの相互コンダクタンスが式1で求められる理由を解説していきたいと思います.まず最初にトランジスタのベース・エミッタ間電圧とコレクタ電流の関係を考えます.
トランジスタのベース・エミッタ間に電圧を加えると,コレクタ電流は指数関数的に増加していきます.そして,トランジスタのベース・エミッタ間電圧(VBE)とコレクタ電流(IC)の関係は式4で表すことができます.
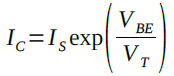 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
ここで,ISは逆方向飽和電流と呼ばれ,トランジスタの大きさなどによって異なり,それぞれ固有の値になります.またVTは,前述した熱電圧で,式5で表されます.
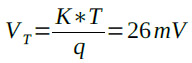 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
図3は,図1右のグラフの横軸を拡大したものです.ここで,ベース・エミッタ間電圧(VBE)が微小に変化したときのコレクタ電流(IC)の微小変化の割合が相互コンダクタンス(gm)です.つまり,コレクタ電流の曲線の傾きが相互コンダクタンスになり,その傾きは図3のようにベース・エミッタ間電圧及びコレクタ電流の大きさによって変わります.
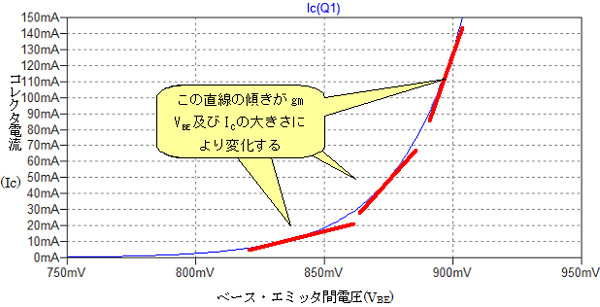
曲線の傾きが相互コンダクタンス(gm)を表している.
微分を使うと曲線の傾きを計算することが可能で,式5をベース・エミッタ間電圧で微分したものが相互コンダクタンスになります.式5をベース・エミッタ間電圧で微分すると式6のようになります.このようにして導出されたのが,式1です.
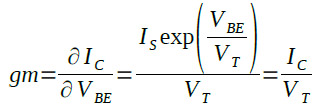 ・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・(6)
式6には各トランジスタ固有の値であるIS(逆方向飽和電流)の項が入っていません.したがって,小さな小信号用トランジスタでも,大きなパワー・トランジスタでも,相互コンダクタンス(gm)は同じ計算結果になります.また,式6で注目すべきポイントは相互コンダクタンスがコレクタ電流(IC)に比例していることです.これはコレクタ電流を変えることで,相互コンダクタンスを任意に変えることができることを意味しており,トランジスタを使った回路設計では,コレクタ電流をいくつに設定するかということが非常に重要になります.
一般的な回路設計で定数設定を行う場合は,必要な相互コンダクタンスから設定すべきコレクタ電流を求める場面が多くなります.その場合は式1を変形した式7を使用することになります.
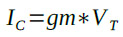 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
●LTspiceで相互コンダクタンスを確認する
図4は,相互コンダクタンスの値をグラフ化するため,図1のグラフをベース・エミッタ間電圧で微分したものです.画面上部の「Ic(Q1)」を右クリックし,「d(Ic(Q1)」に書き換えることで,横軸で微分した結果が表示され,縦軸の単位が自動的にΩ-1に変わります.Ω-1はSと同様に使われる相互コンダクタンスの単位です.
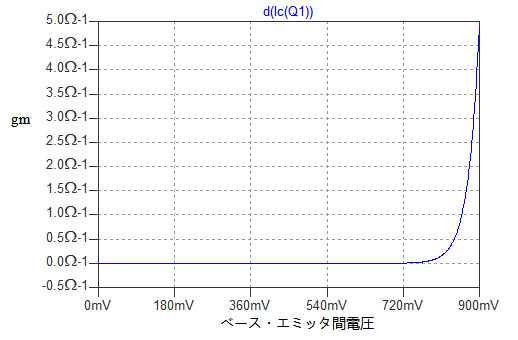
「Ic(Q1)」を右クリックし,「d(Ic(Q1))」に書き換える.
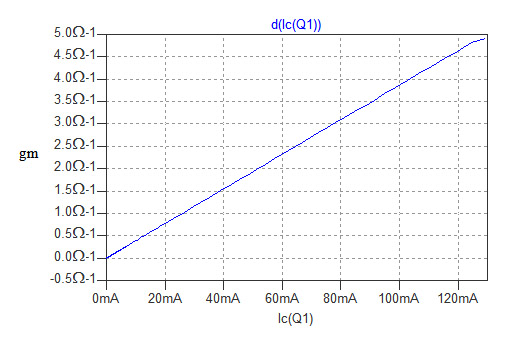
図4では,コレクタ電流と相互コンダクタンスの関係がわからないため,横軸をコレクタ電流に変更します.横軸の数字が表示されていところで左クリックし,「Quantity Plotted」をV2から「Ic(Q1)」に書き換えます.すると図5のようなグラフが表示されます.
横軸の数字が表示されていところで左クリックし,「Quantity Plotted」を変更する.
これで,コレクタ電流と相互コンダクタンスのグラフを表示できました.相互コンダクタンス(gm)がコレクタ電流(IC)に比例していることがよくわかります.ただこのグラフでは電流の小さなときの相互コンダクタンスの値が読みずらいため,縦軸,横軸ともに,対数表示に変更したのが図6です.対数表示にするときは,各軸の数字が表示されていところで左クリックし,「Logarithmic」にチェックを入れます.また,見やすいように横軸の範囲を1u~100m,縦軸の範囲を1e-5~10に変更してあります.
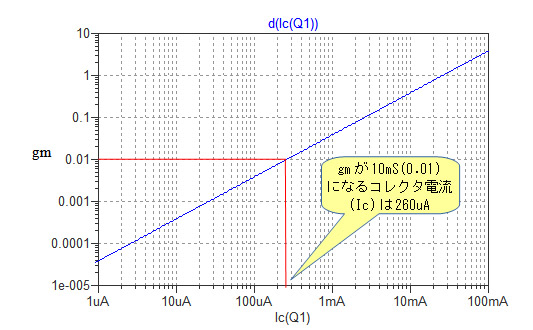
各軸の数字が表示されていところで左クリックし,「Logarithmic」にチェックを入れる
図6から,相互コンダクタンスが10mSになるコレクタ電流の値は260uAとなっていることが読み取れます.これは式1で計算した結果と一致しています.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_005.zip
●データ・ファイル内容
gm1.asc:図1の回路
gm2.asc:図3~図6をシミュレーションするための回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










