矩形波がひずまないのはベッセルとチェビシェフどっち？
図1の回路(a)と(b)は，Sallen-Key2次バターワース・ローパス・フィルタ（LPF）です．二つの回路の違いは，抵抗とコンデンサの値の違いにより特性が変わります．回路(a)がベッセル特性で，回路(b)がチェビシェフ特性になります．この特性の違いにより群遅延（Group Delay）周波数特性に差があります．そこで，この両方の回路に矩形波を入力した場合，出力の波形がひずまないのはどちらでしょうか．
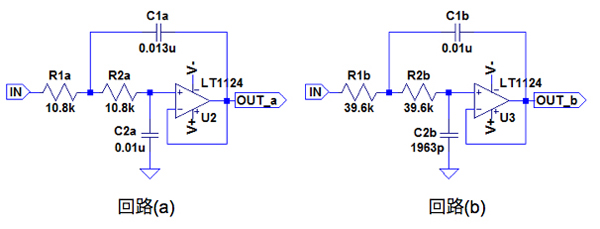
回路(a)がベッセル特性，回路(b)がチェビシェフ特性．
回路(a)
回路(a)は，ベッセル特性のLPFで通過域の群遅延が平坦となる特徴を持ったLPFです．矩形波は振幅と周波数が違う正弦波を合成したもので，群遅延が一定であれば異なる周波数の正弦波を合成しても「うなり（Beat）」はありません．一方，回路(b)は，通過域で2dBのピークを持ったチェビシェフ特性のLPFで，遮断域での減衰はベッセル特性より優れていますが，通過域での群遅延は，平坦でなくうなりが発生し，オーバーシュートやアンダーシュートした応答になります．従って矩形波を入力した場合，出力の波形がひずまないのは，回路(a)となります．
●フィルタ設計は周波数軸と時間軸を考慮する
今回は，フィルタの「ベッセル(Bessel)特性」，「チェビシェフ(Chebyshev)特性」，「バターワース(Butterworth)特性」のゲイン周波数特性や群遅延周波数特性，時間応答のシミュレーションを解説します．通常，フィルタ設計は周波数軸上での特性を考慮しながら回路を作っていくのが一般的です．しかし，時間軸上の出力応答に注意することも大切です．これは，デジタル信号の重畳された雑音をフィルタ回路で取り除くような場合，通過後の波形がひずむことがあるからです．このひずみの原因はフィルタの通過域で群遅延周波数特性が平坦でないことが原因です．
●フィルタ特性は，ベッセル，チェビシェフ，バターワース
フィルタ特性は大きく分けると，ベッセル特性，チェビシェフ特性，バターワース特性に分けられます．本メルマガでも何度か解説した，バターワース特性は，使いやすいフィルタ特性で，通過域でのゲイン周波数特性が平坦です．今回の回路(a)のベッセル特性は，遮断域での減衰は他の二つより劣りますが，通過域の群遅延周波数特性が平坦です．また，回路(b)のチェビシェフ特性は，通過域のゲイン周波数特性は波打ちますが，遮断域での減衰は他の二つより優れています．これから，この三つのフィルタの周波数軸上のゲイン周波数特性と時間軸上の群遅延周波数特性の出力応答を解説します．
●群遅延は「うなり」を評価
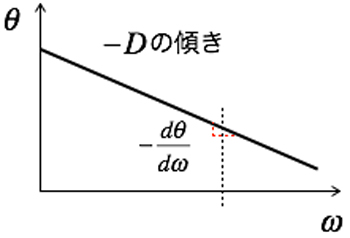
まず，群遅延から説明をしていきます．図2は，矩形波が「遅延D」の回路を通過し，Dだけ遅れた波形を示しています．矩形波はフーリエ変換すると「基本波，2次高調波，3次高調波，…，無限次数の高調波」に分けられ，正弦波の集まりということが分かります．「遅延D」を通過後の波形も，その基本波と高調波が同じ時間だけ遅れれば，無限次数まで正弦波の合成は図2左側の波形と同じになり，波形のひずみはありません．しかし，高調波の遅れ時間に差があると，合成後の波形は，うなりが発生し，オーバーシュートやアンダーシュートした波形になります．これを評価するものが群遅延です．
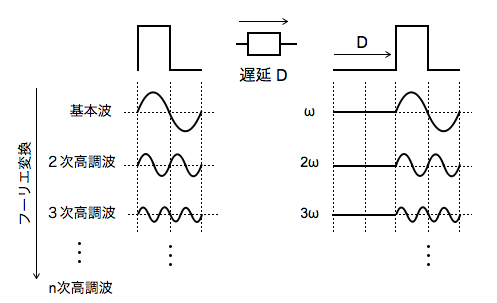
具体的に，図2のフーリエ変換した正弦波の1周期で「遅延D」の入力と出力で考えると，式1が図2の左側の波形，式2が右側の波形となります．式2から式3が求められ，正弦波の位相差（θ）は式4で表させます．
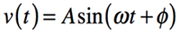・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
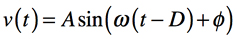・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
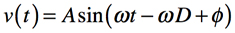・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
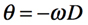・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
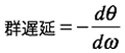・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
次にベッセル特性やチェビシェフ特性，バターワース特性のフィルタを具体的にSallen-Key2次LPFを用いて回路へ実装します．
●ベッセル特性フィルタ
図1の回路(a)のベッセル特性は，最大遅延平坦特性とも呼ばれ，遮断域での減衰はバターワース特性やチェビシェフ特性より劣ります．しかし，通過域の群遅延が平坦であるのが特徴です．ここではベッセル特性の伝達関数とSallen-Key2次LPFの伝達関数から「R1＝R2＝1Ω」とした基準LPFを作ります．次にベッセル特性の伝達関数の絶対値から「ゲイン＝-3.01dB」となる周波数を求め，これらの結果から「遮断周波数＝1kHz」で，「ゲイン＝-3.01dB」として，その時に「C2＝0.01μF」となるスケーリングで具体的な回路を作ります．
図4(a)は，ベッセル特性の基準LPF回路です．図4(a)のC1とC2は，式6の2次ベッセル特性の伝達関数と式7のSallen-Key2次LPFの伝達関数（「R1＝R2＝1Ω」，「ゲインH＝1」）から求めます．その手順は，「式6＝式7」とすると「2/C1＝3」より「C1＝2/3[F]」となり，「1/C1C2＝3」より「C2＝1/2[F]」となります．
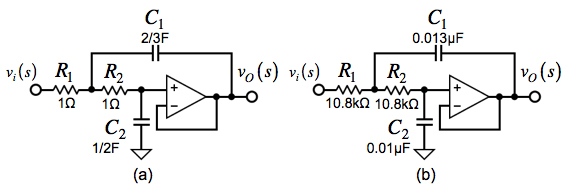
(a) 「R1＝R2＝1Ω」としたベッセル特性の基準LPF回路．
(b) 「遮断周波数＝1kHz」で，「ゲイン＝-3.01dB」，「C2＝0.01μF」とし，残りの素子をスケーリングした回路．
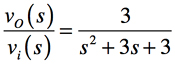・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)
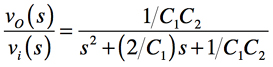・・・・・・・・・・・・・・・・・・・・・・・・(7)
次に式6から「ゲイン＝-3.01dB」になる周波数を求めます．式6を「s＝jω」と置換し，整理したものが式8です．「ゲイン＝-3.01dB」になる周波数を探すため，式8の絶対値をとり「|vo(jω)/vi(jω)|」の「ゲイン＝-3.01dB（1/√2）」としたのが式9です．式9からωCを求めると，式10となります．
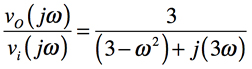・・・・・・・・・・・・・・・・・・・・・・・・・(8)
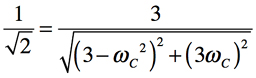・・・・・・・・・・・・・・・・・・・・・・・・・(9)
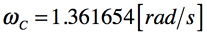・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
以上の結果より，図4(a)を「遮断周波数＝1kHz」で，「ゲイン＝-3.01dB」の時に「C2＝0.01μF」とする周波数スケーリング係数は「kf＝2π(1000)×(1/1.361654)」となり，インピーダンス・スケーリング係数は「km＝（1/(0.01μF×kf)×(1/2)＝10.8×103」となります．
図4(b)は，上で求めたスケーリング係数を使用して，「遮断周波数＝1kHz」で，「ゲイン＝-3.01dB」の時に「C2＝0.01μF」となるように他の素子をスケーリングしたLPF回路です．
●チェビシェフ特性フィルタ
図1の回路(b)のチェビシェフ特性は，振幅波状特性とも呼ばれています．通過域でゲインが波打ちますが，遮断域での減衰が優れるのが特徴です．フィルタの文献などには通過域で波打つゲインのピークの値に対応した素子値が載っています．
図5(a)は，2dBのゲイン・ピークを持ち，「R1＝R2＝1Ω」としたチェビシェフ特性の基準LPF回路です．図5(a)を「遮断周波数＝1kHz」で，その時に「C1＝0.01μF」となる周波数スケーリング係数は「kf＝2π(1000)」となり，インピーダンス・スケーリング係数は「km＝（1/(0.01μF×kf)×(2.4881)＝39.6×103」になります．
図5(b)は，上で求めたスケーリング係数を使用し，「遮断周波数＝1kHz」の時に「C1＝0.01μF」となるように他の素子をスケーリングしたLPF回路となります．ここでチェビシェフ特性の遮断周波数のゲインは，波打つ周波数特性の終端が0dBとなります．
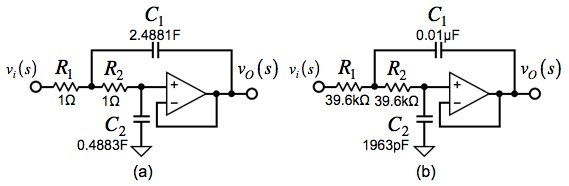
(a) 「R1＝R2＝1Ω」としたチェビシェフ特性の基準LPF回路．
(b) 「遮断周波数＝1kHz｝，「C1＝0.01μF」とし，残りの素子をスケーリングした回路．
●バターワース特性フィルタ
「正しく周波数変換とスケーリングした回路はどっち？」で解説した，バターワース特性は，最大振幅平坦特性とも呼ばれています．通過域でのゲイン周波数特性が平坦であるのが特徴です．
図6(a)は,「R1＝R2＝1Ω」,「遮断周波数（ωC)=1rad/s」で，「ゲイン＝-3.01dB」としたバターワース特性の基準LPF回路です．図6(a)を「遮断周波数＝1kHz」で，その時に「C2＝0.01μF」となる周波数スケーリング係数は「kf＝2π(1000)」で，インピーダンス・スケーリング係数は「km＝（1/(0.01μF×kf)×(0.707)＝11.2×103」となります．
図6(b)は，上で求めたスケーリング係数を使用し，「遮断周波数＝1kHz」で，「ゲイン＝-3.01dB」の時に「C2＝0.01μF」となるように他の素子をスケーリングしたLPF回路です．
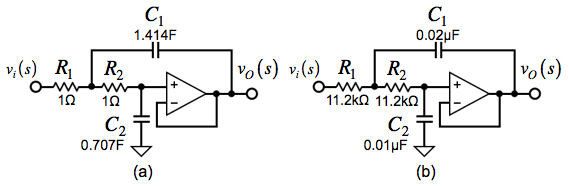
(a) 「R1＝R2＝1Ω」としたバターワース特性の基準LPF回路．
(b) 「遮断周波数＝1kHz｝，「C2＝0.01μF」とし，残りの素子をスケーリングした回路．
●ゲイン周波数特性と群遅延周波数特性をシミュレーションする
図7は，ac解析でゲイン周波数特性と群遅延周波数特性をシミュレーションする回路です．図7(a)がベッセル特性[図1の回路(a)]，図7(b)がチェビシェフ特性[図1の回路(b)]，図7(c)がバターワース特性のSallen-Key2次LPF回路となります．全ての回路の特性は，前述した「遮断周波数＝1kHz」のLPF回路となります．
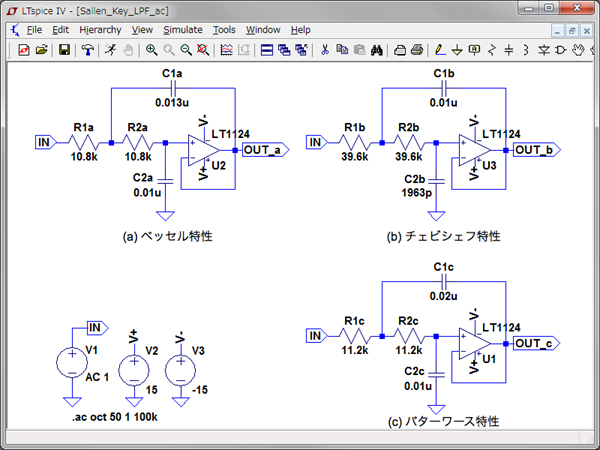
(a)がベッセル特性，(b)がチェビシェフ特性，(c)がバターワース特性．
●ゲイン周波数特性のシミュレーション
図8は，図7のゲイン周波数シミュレーション結果です．通過域のゲインが遮断周波数近くまで0dBとなっているのは，図8(c)のバターワース特性です．図8(a)のベッセル特性は，バターワース特性よりも低い周波数で減衰し始めます．図8(b)のチェビシェフ特性は，通過域でゲインが波打ち，その最大値は2dBであることが分かります．また，遮断周波数（ここでは1kHz）のゲインは，波打つ周波数特性の終端が0dBとなることも分かりました．遮断域での減衰は，他の二つより一番優れています．三つの特性とも遮断周波数より十分高い領域の減衰率は-40dB/decで同じになります．
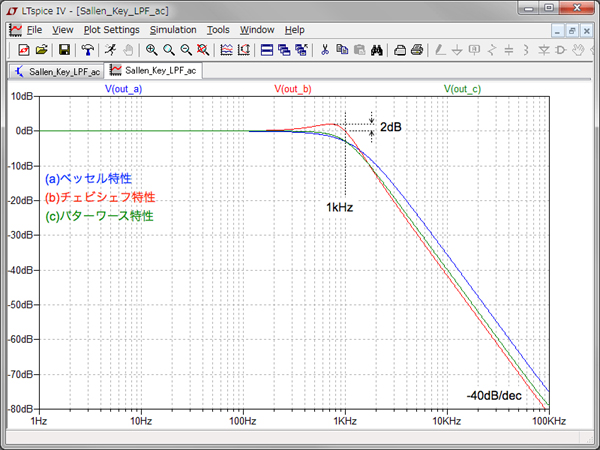
●群遅延周波数特性のシミュレーション
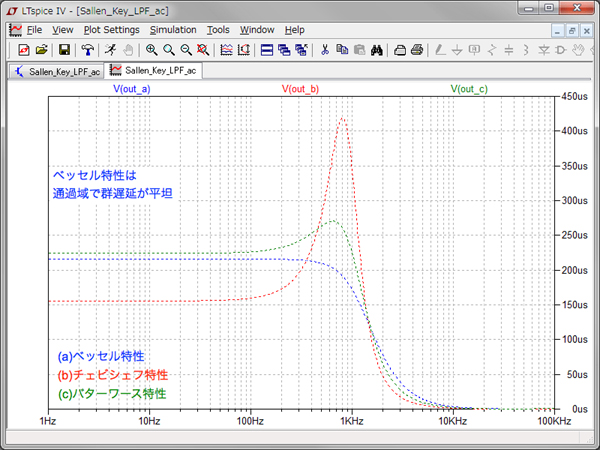
図9は，群遅延周波数特性のシミュレーション結果です．群遅延は，LTspiceの位相特性を示す右側のY軸上で右クリックし，「Representation」を「Group Delay」へ切り替えることにより表示できます．三つの特性を比較すると，通過域での群遅延が平坦なのは図9(a)のベッセル特性です．図9(b)のチェビシェフ特性と図9(c)のバターワース特性は遮断周波近くで群遅延がピークを持つ特性となります．この群遅延周波数特性の時間応答を次で比較します．
●時間応答のシミュレーション
図10は，図10(a)のベッセル特性[図1の回路(a)]，図10(b)のチェビシェフ特性[図1の回路(b)]，図10(c)のバターワース特性の時間応答をシミュレーション(過渡解析)する回路です．入力波形は±1Vの振幅で，立ち上がりと立ち下がり時間は1μsで，周波数を100Hzの矩形波としました．
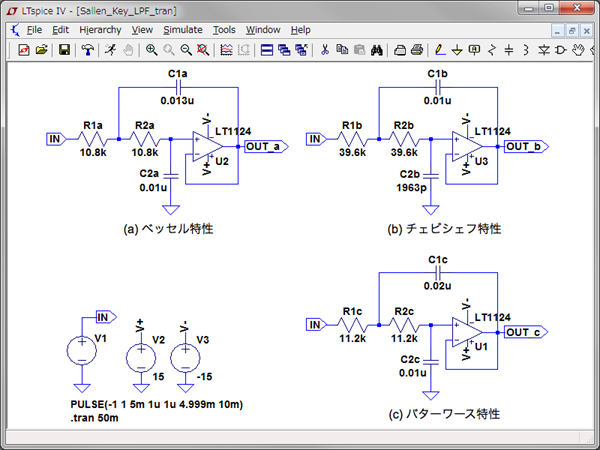
(a)がベッセル特性，(b)がチェビシェフ特性，(c)がバターワース特性．
図11は，図10のシミュレーション結果です．図11(a)がベッセル特性，図11(b)がチェビシェフ特性，図11(c)がバターワース特性です．図9に示した群遅延周波数特性と一緒に比較すると，図9(a)のベッセル特性は，通過域で群遅延が平坦であるため，図11(a)の時間応答はオーバーシュートやアンダーシュートが最も少ない特性であることがわかります．図9(b)のチェビシェフ特性，図9(c)バターワース特性の群遅延は，遮断周波数付近でピークを持つ特性のため，図11の時間応答は立ち上がりと立ち下がりの箇所でうなりが発生し，オーバーシュートやアンダーシュートした応答になります．
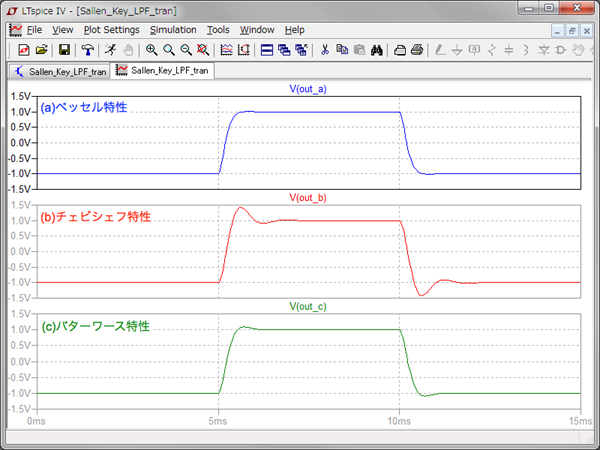
フィルタの設計は，図8の周波数軸上での通過域，遮断周波数，遮断域の特性を考えながら設計するのが一般的です．しかし，図11で示した時間応答も大切です．群遅延での評価，また過渡解析での評価も入れながら設計を進めるといいでしょう．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice041.zip
●データ・ファイル内容
Sallen_Key_LPF_ac.asc：図7の回路
Sallen_Key_LPF_tran.asc：図10の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
