コイルを使わずにバターワース特性が得られる回路はどっち？

■問題

平賀　公久　Kimihisa Hiraga

　図1の回路(a)と(b)は，図1上段（左）の遮断周波数(ω_C)を1rad/sに正規化したR-R型2次バターワース・ローパス・フィルタ（LPF）の特性をコイルを使用せずに実現した回路です．
　実現するには，Bruton変換で，コイルを抵抗に置き換え[図1上段（右）]て，D素子をGICのFDNRで実装しました．また，遮断周波数(f_C)を1kHzとするため，全てのコンデンサを0.01μFへ変更し，抵抗をスケーリングしています．
　回路(a)と(b)の違いは，回路(a)のC_Z5aと回路(b)のR_Z5bになり，その他の受動素子，OPアンプは同一です．この場合，遮断周波数(f_C)が1kHzの「FDNR2次バターワースLPF回路」は，回路(a)と(b)のどちらでしょうか．

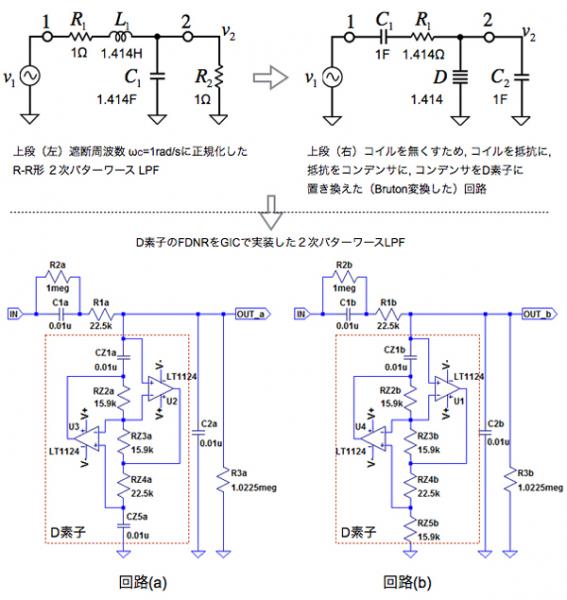
図1上段（左）　遮断周波数(ω_C)を1rad/sに正規化したR-R型2次バターワースLPF
図1上段（右）　Bruton変換で，コイルを無くした回路図
図1　問題のFDNR2次バターワースLPF回路(a)と(b)

■解答

回路(a)
　今回のポイントは，コイルを使わずにフィルタを構成するため，Bruton変換で，「コイルを抵抗」，「抵抗をコンデンサ」，「コンデンサをD素子」に置き換えます．このとき変換されたD素子は，負の抵抗のような「世の中に存在しない素子」を示します．このD素子は，FDNR（Frequency Dependent Negative Resistor：周波数依存型負性抵抗）と呼ばれ，GIC（Generalized Impedance Converter：一般化インピーダンス変換器）を用いて実現します．
　赤破線で囲ったD素子のインピーダンスは，1/s²C（s＝jω）とするため，GICの入力インピーダンスを調整します．ここでGICの入力インピーダンスは「Z_IN＝(Z₁Z₃Z₅)/(Z₂Z₄)」で表されます．このZ₁を「C_Z1a，C_Z1b」，Z₂ を「R_Z2a，R_Z2b」，Z₃を「R_Z3a，R_Z3b」，Z₄を「R_Z4a，R_Z4b」，Z₅を「C_Z5a，R_Z5b」としたとき，1/s²Cのインピーダンスを得るには，Z_INの分子項（Z₁Z₃Z₅）には，二つのコンデンサ(C＝1/sC)が必要となります．そこで，これを満たしているのは回路(a)となります．

■解説

　今回は，「バターワース特性を得られる回路はどっち？」の続編となります．バターワース特性やスケーリングについては，前回の解説をご参照ください．

●コイルを使わずにフィルタを構成する
　コイルとコンデンサで構成する「はしご型フィルタ」は，受動素子だけで作製でき，電源がいらないフィルタとして高周波回路で現在も使われています．しかし，はしご型フィルタを低周波で使用する場合，受動素子の値が大きくなります．特にコイルは素子の値を大きくすると，巻き数が増えて物理的に大きくなり，また巻線の直列抵抗が増えることからQ値（Quality Factor）が低下するので実用的ではありません．
　低周波へ応用するには，コイルを回路で実現したり，また，今回紹介する，FDNRのD素子のように，世の中に存在しない素子を回路で実現する手法があります．この手法の一つがGICです．これらを使用して，はしご型フィルタの特性を実現できる回路が作れます．
　コイルを使わずにフィルタを構成するため，まず，抵抗やコイル，コンデンサを図2のように1/sを乗じて変換することをBruton変換といいます．「抵抗をコンデンサ」，「コイルを抵抗」，そして，「コンデンサをD素子」に変換する方法です．

図2　抵抗やコイル，コンデンサをBruton変換した結果
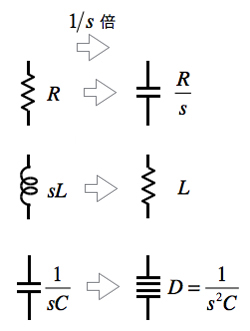
「抵抗をコンデンサ」，「コイルを抵抗」，「コンデンサをD素子」に変換する．

　具体的な例が図3で，図3(a)は「R-R型2次バターワースLPF」であり，各素子へ1/sを乗じると図3(b)の「FDNR2次バターワースLPF」になります．このように回路を変換しても図3(a)と(b)のフィルタの伝達関数(v₂/v₁)は，式1で変わりません．Bruton変換でできたD素子は，1/s²Cの項を持つFDNRで，これが回路で実現できれば図3(a)と(b)の周波数特性は同じになります．このような，FDNRの概念はL. T. Brutonにより発表されました．

図3　Bruton変換前の回路と変換後の回路
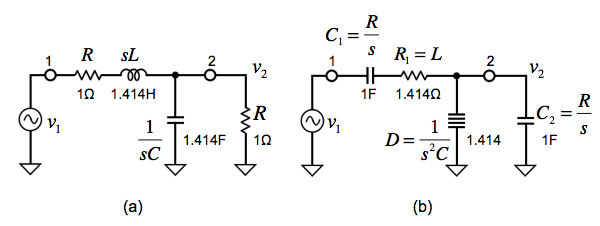
(a)　R-R型2次バターワースLPF回路
(b)　(a)をBruton変換したFDNR2次バターワースLPF回路

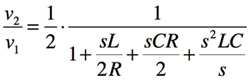・・・・・・・・・・・・・・・・・・・・・・・・(1)

●D素子は2個のOPアンプと5個の受動素子で構成
　GICは，A．Antoniouが発表した，一般化インピーダンス変換器です．図4の回路がGICで，2個のOPアンプと5個の受動素子で構成しています．GICは，端子AとGND間のインピーダンスを5個の受動素子の組み合わせで変化させます．GICは，フィルタ回路において信号ラインとGND間に接続される素子の代わりに使用でき，ここでは，図3(b)にあるD素子を回路で作成しています．

図4　A．Antoniouが発表したGIC
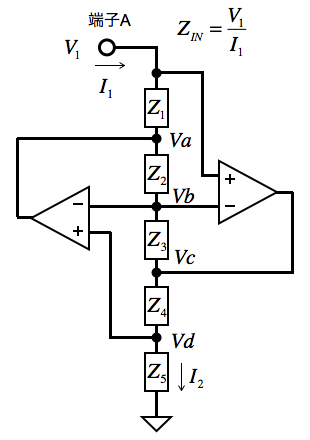
2個のOPアンプと5個の受動素子で構成．

　次に図4のGICの端子Aからみた入力インピーダンスを求めます．OPアンプは理想と考え，非反転端子と反転端子がバーチャル・ショートであること，また，Z₁からZ₅まで流れる電流は等しいとして，式2～式6が成り立ち，整理をすると式7で表せます．

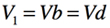・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

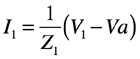・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

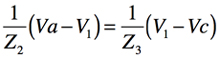・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

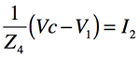・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

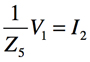・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

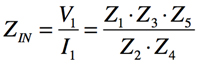・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

●GICを使用してFDNRを実現
　Bruton変換した図3(b)の「C₁が1F」，「R₁が1.414Ω」，「C₂が1F」は，そのままの値で，D素子の1/s²(1.414)を図4のGICを使用して作ります．D素子は，1/s²の項がつくことから，その入力インピーダンスを表すZ_INの分子項（Z₁Z₃Z₅）には，二つのコンデンサ(C＝1/sC)が必要となります．
　ここでは，図5のようにZ₁とZ₅はコンデンサ（C_Z1，C_Z5），残りの3個の素子を抵抗(R_Z2，R_Z3，R_Z4)としました．この場合，図4の端子Aからみた入力インピーダンスは，式7より（1/s² C_Z1C_Z5）×（R_Z3 /R_Z2R_Z4）の値を持つD素子へインピーダンス変換されます．全てのコンデンサを0.01μFを使うことが前提なので，図5のコンデンサは図3(b)のC₁，C₂に合わせて「C_Z1＝C_Z5＝1F」にします．
　またD素子の1/s²(1.414)を作るため，抵抗は，R_Z2を1Ω，R_Z3を1Ω，R_Z4を1.414Ωとしました．まとめると式8となります．このようにしてD素子が実現できました．

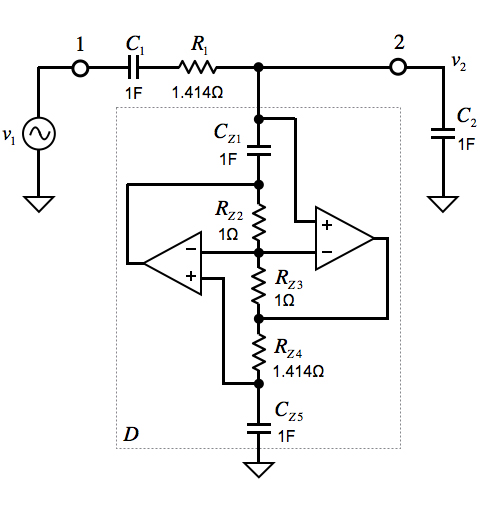
図5　図3(b)のD素子をFDNRを使用したFDNR2次バターワースLPF回路
遮断周波数 ω_C＝1rad/sで正規化されている．

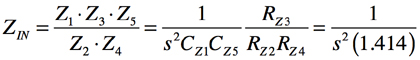・・・・・・・・・・・・・(8)

●FDNRを実現したら次はスケーリング
　図5は，遮断周波数（ω_C）を1rad/s(ω_C＝2πf_C)で正規化された回路です．これを元に全てのコンデンサを0.01μFとし，遮断周波数（f_C）を1kHzになるようスケーリングします．具体的には遮断周波数「ω_C＝1rad/s」を「f_C＝1kHz」とする周波数スケーリング係数は，「k_f＝2π(1000)＝6.28×10³」です．また，全てのコンデンサを0.01μFとしたときのインピーダンス・スケーリング係数は，「k_m＝1/(k_f×0.01×10^-6)＝15.9×10³」となります．
　したがって，図5の回路をスケーリングすると，R₁とR_Z4は「1.414Ω×k_m＝22.5kΩ」，R_Z2とR_Z3は「1Ω×k_m＝15.9kΩ」となり，図6になります．

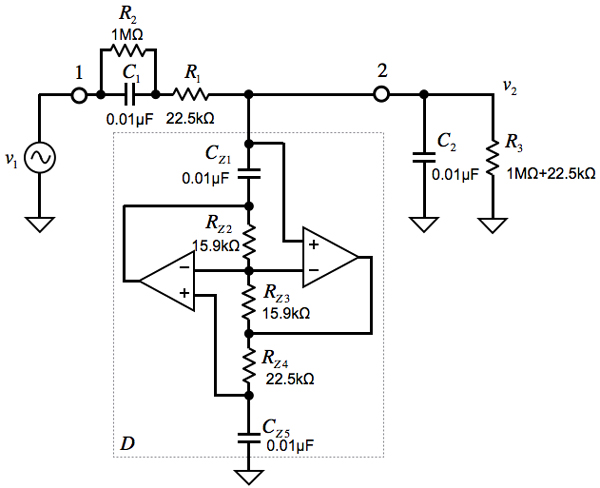
図6　図5を遮断周波数(f_C)を1kHz，全てのコンデンサを0.01μFとしてスケーリングした回路

　図6には，図5にないR₂とR₃を新たに入れています．これはBruton変換したC₁のコンデンサは，直流を通さないためLPFになりません．その対策でC₁と並列にR₂を入れています．また，R₃はR₂を追加したとき，端子2のフィルタの出力において，直流でのゲインが-6.02dB(1/2倍)となるように選び，「R₁+R₂＝1MΩ+22.5kΩ」とします．R₁とR₂の値が小さいとフィルタ特性が変わりますので，シミュレーションで確かめながら値を決めるのがいいでしょう．

●FDNR2次バターワースLPFの特性をLTspiceで確かめる
　図7(1)は，図1上段(左)のR-R型2次バターワースLPFの回路です．図7(2)と(3)は，図1の回路(a)と(b)の周波数特性を調べる回路です．図7(1)はBruton変換前の回路で，周波数特性を比較するために入れました．シミュレーションはAC解析を実行し，図7(1)，(2)，(3)の出力のゲイン周波数特性をシミュレーションします．

図7　(1)～(3)の周波数特性をシミュレーションする回路
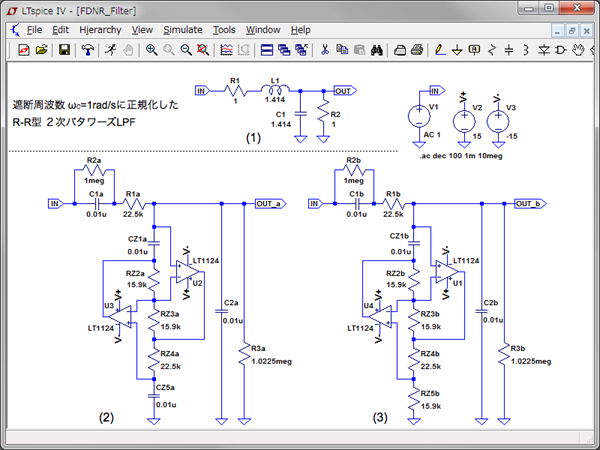
(1)　遮断周波数ω_C＝1rad/sに正規化したR-R型2次バターワースLPF回路
(2)　図1回路(a)の回路
(3)　図1回路(b)の回路

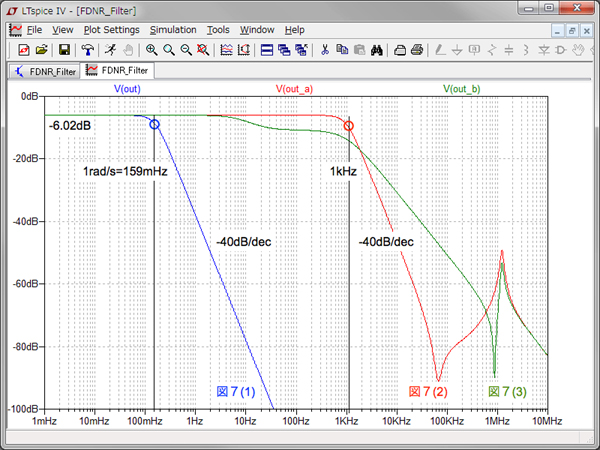
　図8は，図7のシミュレーション結果です．青線で示した図7(1)のゲイン周波数特性は，R-R型2次バターワースLPFの周波数特性です．低周波から遮断周波数手前までは，-6.02dBの平坦なゲインで，遮断周波数は「1rad/s＝159mHz」にあります．遮断周波数より高い周波数では，-40dB/decの減衰となります．
　赤線で示した図7(2)は，全てのコンデンサを0.01μFとして，遮断周波数を1kHzとしたFDNR2次バターワースLPFのゲイン周波数特性です．図7(1)の青線が周波数軸上で右側へシフトしています．100kHz以上でゲイン周波数特性が波打っているのはOPアンプによる影響です．
　緑線で示した図7(3)は，図1の回路(b)で，GICにコンデンサは1個（C_Z1b）ですのでD素子にならず，特性がずれているのがわかります．

図8　図7のシミュレーション結果

　今回は，R-R型2次バターワースLPFを例にしましたが，さらに高次のフィルタでも応用できます．電源が必要ないLCフィルタの利点は失われますが，低周波用途の回路で大きな値のコイルを使わずに，はしご型フィルタが実現できるので魅力的な回路です．遮断周波数をω_Cヘ正規化したフィルタの設計表も多くの文献で公開されています．それらを元に「Bruton変換」，「FDNRの実現」，「スケーリング」の手順で設計できますので，ぜひ一度試してください．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice037.zip

●データ・ファイル内容
FDNR_Filter.asc：図7の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください