バターワース特性を得られる回路はどっち？

■問題

平賀　公久　Kimihisa Hiraga

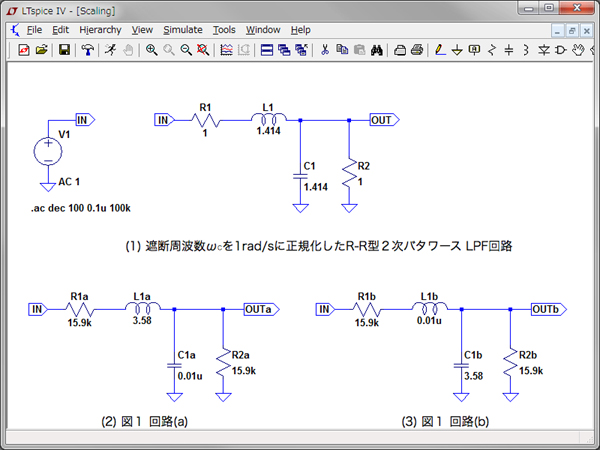
　図1下段の回路(a)と(b)は，図1上段の遮断周波数(ω_C)を1rad/sに正規化した「R-R型2次バターワース（Butterworth）ローパス・フィルタ（LPF）」を元に，R₁とR₂を15.9kΩへ変更し，かつ遮断周波数(f_C)を1kHzとするため，L（コイル）とC（コンデンサ）の値をスケーリングしました．回路(a)と(b)の違いはLとCの値が入れ替わっています．R-R型2次バターワースLPFの特性を変えずにR₁とR₂が15.9kΩの条件で，遮断周波数(f_C)が1kHzとなる回路はどちらでしょうか．

図1　問題のR-R型2次バターワースLPF回路
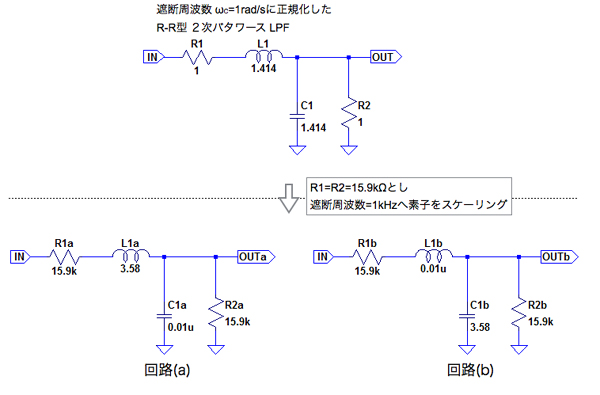
基準となる遮断周波数(ω_C)が1rad/sのR-R型2次バターワースLPF（上段）を元に
回路(a)と(b)は，R₁とR₂が15.9kΩで，LとCの値が入れ替わっている．

■解答

回路(a)
　インピーダンス・スケーリングの係数（k_m）は，R₁とR₂の抵抗値を1Ωから15.9kΩにすることから，「k_m=15.9×10³」です．また，遮断周波数を1rad/sから1kHzとする周波数スケーリングの係数(k_f)は，「k_f=2π(1000)」です．この二つの係数から，スケーリング後のL（L_SCALE）は「L_SCALE=(k_m/k_f)L_NOR=3.58H」（L_NORはスケーリング前のL）となります．スケーリング後のC(C_SCALE)は，「C_SCALE=(1/k_mk_f)C_NOR=0.01μF」（C_NORは，スケーリング前のC）となります．この数値から，回路(a)がR-R型2次バターワースLPFの特性を変えずにR₁とR₂が15.8kΩ，遮断周波数(f_C)が1kHzを得られる回路となります．

■解説

●R-R型，はしご型，バターワース特性について
　まず，図1のコイル(L)とコンデンサ(C)で構成される「はしご型」のフィルタは古くから使われている回路です．また，入力と出力が抵抗(R)で終端されている回路は，「R-R型」と呼ばれ，整合周波数で最大電力が供給されます．バターワース特性のはしご型フィルタ設計では，遮断周波数（ω_C）は1rad/sを基準として，素子値の値を算出し，インピーダンス・スケーリングと周波数スケーリングを行います．
　この素子値は，次数が高くなると計算が大変なので，フィルタに関する文献などに掲載されている「バターワース・フィルタの素子値表」などを使って値を算出していくのが一般的です．
　次に，バターワース特性とは，英国の技術者Stephen Butterworth（スティーブン・バターワース）が1930年に論文で発表した「バターワース・フィルタ」の特性です．フィルタの特性は，遮断周波数を境に，通過域と遮断域があります．LPFを例にとると，遮断周波数より低い周波数は通過（通過域）させ，また，遮断周波数より高い周波数では減衰（遮断域）させます．この通過域や遮断域の特性によりバターワース特性と呼ばれています．同じように「チェビシェフ特性」や「ベッセル特性」など発明者の名前が付いているフィルタ特性があります．
　図2は，図1上段のシミュレーション結果です．バターワース特性として直流の場合，コイルは短絡で，コンデンサは開放となります．その時，入出力にある二つの同じ値の抵抗(R-R型)により，ゲインは分圧され－6.02dB（1/2倍）になり，通過域のゲイン周波数特性は平坦になります．遮断周波数によるゲインの減衰は，直流時の減衰から－3.01dBとなります．遮断周波数より高い遮断域では－20×n[dB/dec]（nは次数）で－40dB/decの減衰特性となります．ここでは示しませんが，チェビシェフ特性は通過域でのゲインが波打ち，遮断域での減衰はバターワース特性より急峻です．

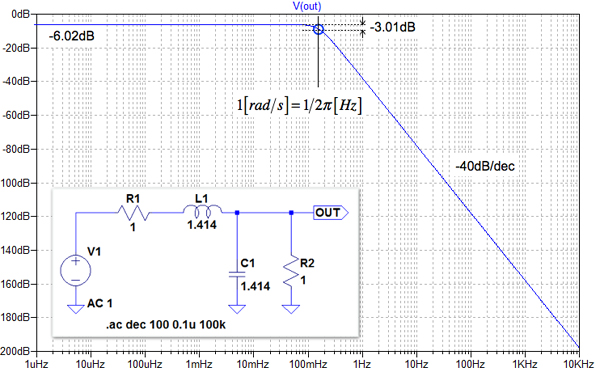
図2　図1上段で遮断周波数(ω_C)を1rad/sに正規化したスケーリング前のR-R型2次バターワースLPFを
シミュレーションした結果

●伝達関数を計算し，バターワース特性を確かめる
　図3は，図1上段のR-R型2次バターワースLPFから，伝達関数でバターワース特性を導くため，コイル(L)とコンデンサ(C)の値を求める式や端子を示した図です．図1上段と同じように，遮断周波数（ω_C）は1rad/sを基準としています．Rが1で，ω_Cが1rad/sの時，LとCは1.414となります．LとCの分子にある√2は2次のバターワース特性からくるものです．

図3　R-R型2次バターワースLPFの回路
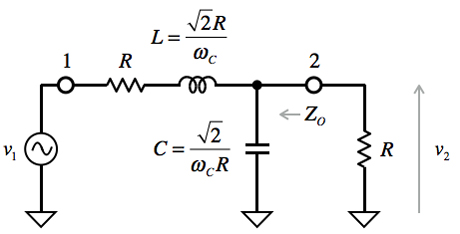
伝達関数でバターワース特性を導くため，LとCの値を求める式や端子を示した．

　また，図2で周波数特性をシミュレーションした通り，図1のバターワース特性の通過域のゲイン周波数特性は－6.02dB（1/2倍）で平坦です．遮断周波数でゲインの減衰は，－6.02dBからさらに－3.01dB減衰し，遮断域では－20×n[dB/dec]（nは次数）の減衰特性でした．
　これらの特性から，伝達関数を計算し，バターワース特性を確かめてみます．回路の計算は，「鳳（ホウ）テブナンの法則」を用います．端子2に接続されているRを外し，そのときの端子2の開放電圧(v’)と端子2からみたインピーダンス(Z_O)を求めます．その後，端子2のRを接続したときの電圧の関係「v₂=R/(Z_O+R)×v’」より伝達関数「(v₂/v₁)」を求めます．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

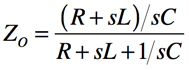・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

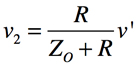・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

(1)式，(2)式を(3)式へ代入します．

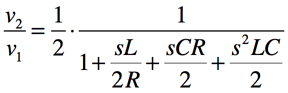・・・・・・・・・・・・・・・・・・・・・・・(4)

　ここで，図3のコイルとコンデンサの素子値である「L=√2R/ω_C」と「C=√2/ω_CR」を式4へ代入します．その絶対値をとると，ゲインの周波数特性を表す式5が得られます．これがLPFのゲイン周波数特性を示しており，ωをスイープさせるとω_Cを境にゲインが変わる特性であることがわかります．

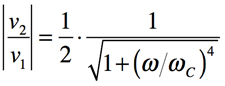・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　式5より，ω_Cを境にした三つの状態は，「通過域（ω<<ω_C）」，「遮断周波数（ω=ω_C）」，「減衰域（ω>>ω_C）」となり，この状態のゲインを調べます．

1）通過域（ω<<ω_C）のとき
　式5において，「1>>(ω/ω_C)⁴」の場合，分母の近似は1であり，そのゲインは，
|v₂/v₁|dB=20log₁₀(1/2)=－6.02dB
低周波のゲインは－6.02dBです．

2）遮断周波数（ω=ω_C）のとき
|v₂/v₁|=1/2×1/√2となり，
|v₂/v₁|dB=20log₁₀(1/2)－20log₁₀(1/√2)
　　　　　=－6.02dB－3.01dB
通過域のゲインである－6.02dBより，さらに－3.01dB減衰したところが遮断周波数です．

3）遮断周波数より高い周波数（ω>>ω_C）のとき
|v₂/v₁|dB=20log₁₀(1/2)－20log₁₀(ω/ω_C)²
　　　　　=-6.02dB－40log₁₀(ω/ω_C)
遮断周波数より高い周波数では－40dB/decの傾きで減衰します．

　式5から1），2），3）のように，図2のシミュレーションと同じ値を計算からも導き出せます．また，式5の「R-R型」のゲイン（1/2倍）を取り除き，遮断周波数に関する項をまとめると式6になります．式6が，通過域のゲインが1倍で，n次バターワース特性を示した伝達関数です．LPFの伝達関数が式6の形になるのがバターワース特性となります．

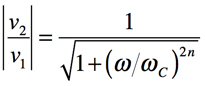・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

●インピーダンス・スケーリングと周波数スケーリングについて
　フィルタのスケーリングは，インピーダンス・スケーリングと周波数スケーリングがあり，これらを使って元となる遮断周波数(ω_C)を1rad/sに正規化した回路から所望の回路へ変えていきます．スケーリングの方法としては，次のA)，B)，C)が挙げられます．

A)　インピーダンス・スケーリングのみ使用
　フィルタの特性と遮断周波数を変えずに，コンデンサを1μFへ変更したい．他の素子をインピーダンス・スケーリングする．

B)　周波数スケーリングのみ使用
　フィルタの特性を変えずに，遮断周波数を10Hzにしたい．インピーダンスが周波数に依存する素子を周波数スケーリングする．

C)　インピーダンスと周波数のスケーリング両方を使用
　フィルタの特性を変えずに，抵抗を15.9kΩへ変更し，さらに遮断周波数を1kHzにしたい．他の素子をインピーダンス・スケーリング，周波数スケーリングする等です．

　今回の問題で使用したスケーリングは，C）になります．C）のインピーダンスと周波数のスケーリング両方を使用する方法が三つの中でよく使用されます．ここではA)，B)，C)の三つの方法を順にシミュレーションで確認していきます．
　図4にインピーダンス・スケーリング，周波数スケーリング，またインピーダンスと周波数の両方をスケーリングする一覧を載せました．「R_SCALE」，「L_SCALE」，「C_SCALE」はスケーリング後の値です．「R_NOR」，「L_NOR」，「C_NOR」はスケーリング前の値となります．またk_mはインピーダンス・スケーリングの係数で，k_fは周波数スケーリングの係数です．
　インピーダンス・スケーリングは素子のインピーダンスR，|Z_L|（コイルの絶対値），|Z_C|（コンデンサの絶対値）をk_m倍へ変化させることです．周波数スケーリングは，「|Z_L|＝ωL，|Z_C|=1/ω_C」のインピーダンスを変えずにk_f倍だけωを変化させることであり，k_f倍の周波数の変化分を素子値で調整していると考えればわかりやすいでしょう．

図4　インピーダンス・スケーリング，周波数スケーリングの式
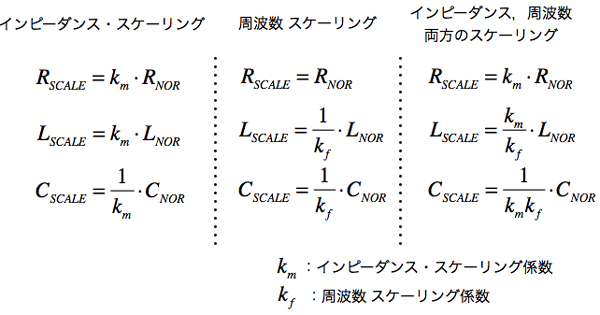
　　　k_mはインピーダンス・スケーリングの係数，k_fは周波数スケーリングの係数

●インピーダンス・スケーリングを使用した場合
　インピーダンス・スケーリングのみを使用した解説をします．遮断周波数（ω_C）を1rad/sに正規化したR-R型2次バターワースLPFの定数（R₁=R₂=1，L₁=C₁=1.414）を元にインピーダンス・スケーリングし，その結果をシミュレーションで確かめます．元となる回路のコンデンサは1.414Fなので，図4の式を使用して求めたインピーダンス・スケーリング係数は「k_m=C_NOR/C_SCALE=1.414F/1μF=1.414×10⁶」です．このk_mを用いてR_SCALEとL_SCALEを同じようにインピーダンス・スケーリングすると，R_SCALE =1.414MΩ，L_SCALE=2MHとなります．
　図5は，インピーダンス・スケーリングをシミュレーションする回路です．図5(1)は，図5(2)と比較するのための回路で，遮断周波数（ω_C）を1rad/sに正規化したR-R型2次バターワースLPF回路です．図5(2)は，インピーダンス・スケーリングで求めた素子値を代入した回路です．

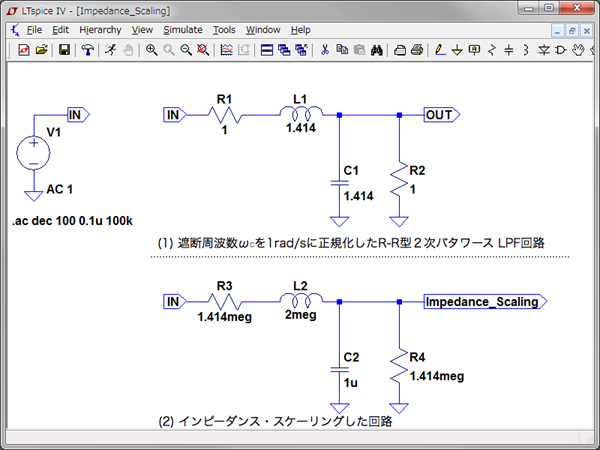
図5　フィルタの特性を変えずに，コンデンサを1μFへ変更し，他の素子をインピーダンス・
スケーリングしたシミュレーション回路

　図6は図5のシミュレーション結果で，二つの回路のゲイン周波数特性は重なっており，バターワース特性のゲイン周波数特性を変えずに，コンデンサを1μFへ変更できています．

図6　図5のシミュレーション結果
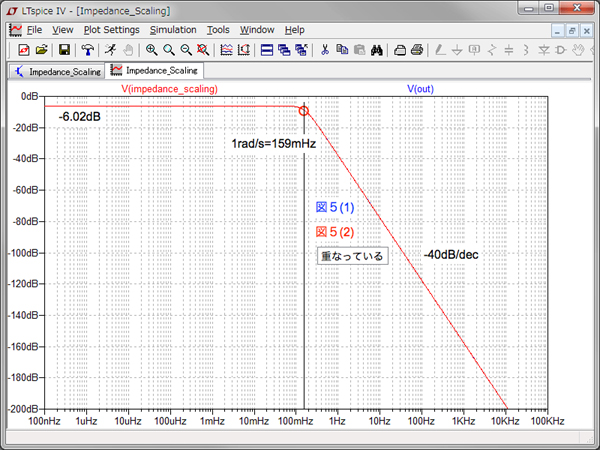
二つの回路のゲイン周波数特性は重なっている．

●周波数スケーリングを使用した場合
　次に，周波数スケーリングのみを使用した解説をします．遮断周波数(ω_C)を1rad/sに正規化したR-R型2次バターワースLPFの定数（R₁=R₂=1， L₁=C₁=1.414）を元に周波数スケーリングし，その結果をシミュレーションで確かめます．
　元となる回路の遮断周波数(ω_C)1rad/sを10Hzにするために「ω_C=2πf_C」の関係より，周波数スケーリング係数は「k_f=2π(10)」となります．このk_fを使って図4の周波数スケーリングの式よりR_SCALE，L_SCALE，C_SCALEを求めると，抵抗値は周波数に依存しないので，R_SCALEの値は変わりません．L_SCALEの値は22.5mHとなり，C_SCALEの値は22.5mFとなります．
　図7は，周波数スケーリングをシミュレーション回路です．図7(1)は，図7(2)と比較するための回路で，遮断周波数（ω_C）を1rad/sに正規化したR-R型2次バターワースLPF回路です．図7(2)は周波数スケーリングで求めた素子値を代入した回路です．

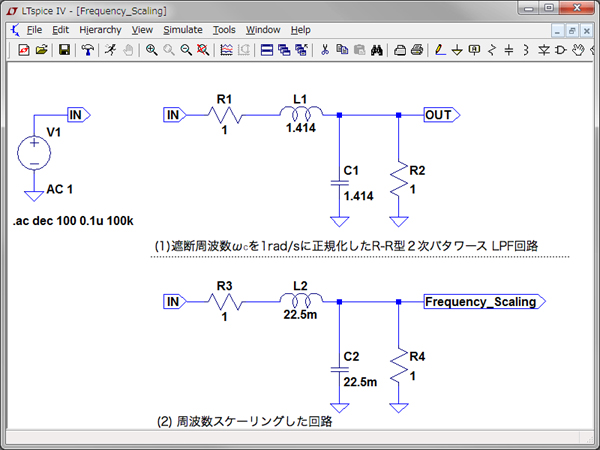
図7　フィルタの特性を変えずに，遮断周波数を10Hzにする，各素子を周波数スケーリングした
シミュレーション回路

　図8は図7のシミュレーション結果で，バターワース特性の通過域のゲインは，－6.02dBで，遮断域の減衰も－40dB/decのままで，遮断周波数を10Hzへ移動できています．

図8　図7のシミュレーション結果
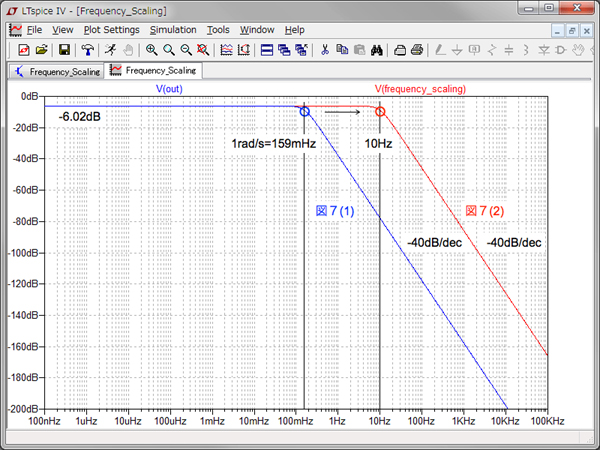
遮断周波数を10Hzへ移動できている．

●インピーダンスと周波数のスケーリング両方を使用した場合
　最後に，インピーダンスと周波数の両方を使用したスケーリングを解説します．この方法で図1のスケーリングを行っています．遮断周波数(ω_C)は，1rad/sに正規化したR-R型2次バターワースLPFの定数（R₁=R₂=1，L₁=C₁=1.414）を元にインピーダンス，周波数を両方スケーリングし，その結果をシミュレーションで確かめます．
　図9は，インピーダンスと周波数のスケーリング両方をシミュレーションする回路です．図9(1)は，図1上段の回路で，図9(2)(3)と比較するための回路です．遮断周波数(ω_C)が1rad/sに正規化したR-R型2次バターワースLPF回路となります．図9(2)は，図1回路(a)と同じで，解答に示した素子値を代入した回路です．図9(3)は，図1回路(b)でLとCのスケーリングの値を入れ違えた回路です．

図9　フィルタの特性を変えずに，抵抗を15.9kΩへ変更し，更に遮断周波数を1kHzにし，
他の素子をインピーダンス・スケーリング，周波数スケーリングするシミュレーション回路

　図10は図9のシミュレーション結果で，図9(2)は，バターワース特性の通過域のゲインが－6.02dBで，遮断域の減衰が－40dB/decのまま，抵抗（R）を15.9kΩへ変更し，遮断周波数を1kHzへ移動できました．LとCを入れ替えた図9(3)は，適切なスケーリングでないためにフィルタの特性や遮断周波数が目的から大きく外れていることがわかります．

図10　図9のシミュレーション結果
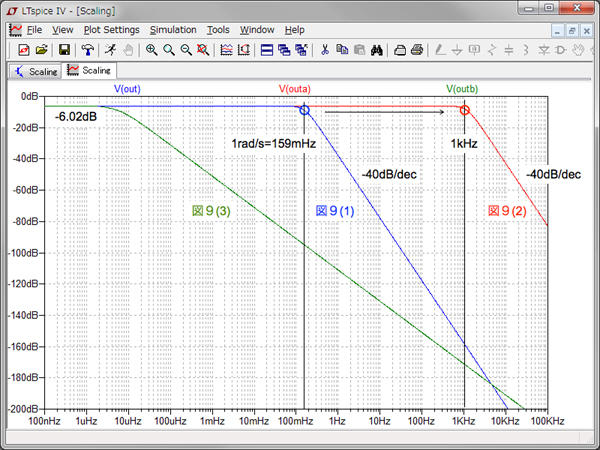
図9(2)[回路(a)]は，バターワース特性のまま，遮断周波数を1kHzへ移動できた．
図9(3)[回路(b)]は，適切なスケーリングでないため，フィルタの特性や遮断周波数が目的から外れている．

　今回は，コイルやコンデンサの受動部品の値を変更し，2次バターワースLPFの特性を得る，インピーダンスと周波数のスケーリングを解説しました．はしご型フィルタは，抵抗やコイル，コンデンサの受動部品で構成する他に，FDNR(Frequency Dependent Negative Resistance) やGyrator（ジャイレータ）を使用して，コイルを等価的に作り，2次バターワースLPFの特性を得る方法もあります．このような設計において，遮断周波数(ω_C)を正規化した値を元に，インピーダンスと周波数スケーリングを使い，回路を仕上げていくのは便利です．次回（LTspice電子回路マラソン037）は，オペアンプでFDNRを構成し，コイルを使用せず，R-R型2次バターワースLPFの特性を実現するスケーリングを解説します．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice035.zip

●データ・ファイル内容
Impedance_Scaling.asc：図5の回路
Frequency_Scaling.asc：図7の回路
Scaling.asc：図9の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください