全波整流出力が得られる回路はどっち？

■問題

小川　敦　Atsushi Ogawa

　図1の回路(a)と(b)は，OPアンプを使用した整流回路です．回路(a)と(b)の回路形式は全く同じですが，定数が一部異なります．回路(a)のR3は10kΩで，回路(b)のR3は20kΩとなっています．OPアンプの電源は±2.5Vで，入力信号は信号電圧が2Vppで1kHzの正弦波を加えます．この条件で出力に，全波整流波形が出力されるのは回路(a)と(b)のどちらの回路でしょうか．

図1　問題の整流回路
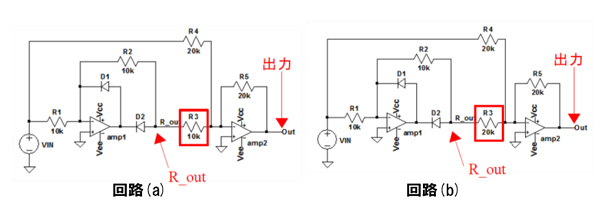
回路(a)はR3が10kΩで，回路(b)はR3が20kΩ．

■解答

回路(a)
　回路(a)と(b)ともにR_outには入力信号と位相が反転した半波整流波形が出力されます．この半波整流出力を2倍したものと，入力信号を加算すると，出力には全波整流波形が出力されます．回路(a)のR_outのゲインは，「R5/R3=2」なので半波整流波形は2倍されます．回路(b)のR_outは，「R5/R3=1」なのでゲインは1倍です．したがって，全波整流波形が出力されるのは回路(a)になります．

■解説

●整流回路は，交流電源から直流電源を作る
　回路の解説をする前に，まず，半波整流波形と全波整流波形について解説します．整流回路は，交流電源から直流電源を作る時に使用します．オーディオ用回路などで信号の大きさを知りたい時にも使用されます．信号を整流してからコンデンサで平滑して直流信号に変換することで，信号の大きさに比例した直流電圧が得られます．
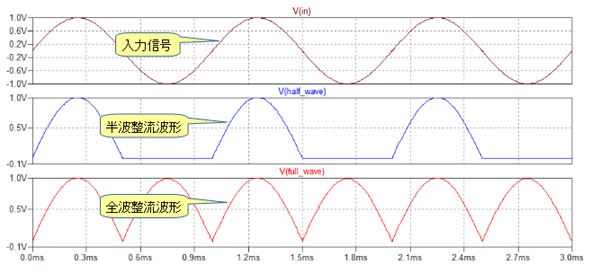
　図2の半波整流波形と全波整流波形を比べるとわかるように，半波整流波形のリップル電圧の周波数が入力信号と同じなのに対し，全波整流波形はリップル電圧の周波数が入力信号の2倍になっています．これは，全波整流の場合はコンデンサで平滑する時に，半波整流よりも小さい時定数で平滑化できることを意味します．そのため，すばやい応答が必要な時には全波整流を選択することになります．

図2　半波整流波形と全波整流波形

●整流回路にOPアンプを使用する理由
　次に，整流回路にOPアンプを使用する理由について解説します．図3はダイオードを使用した単純な整流回路です．入力信号は1kHzの正弦波とし，LTspiceの「.stepコマンド」で振幅を0.4Vppと2Vppに変化させています．

図3　ダイオードによる半波整流回路

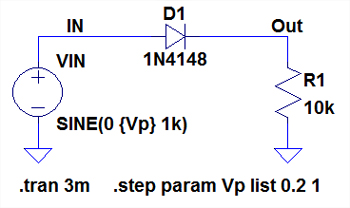
　図4はこの回路をLTspiceでシミュレーションしたものです．図4の上段が入力信号の波形で，下段が，出力信号[V(out)]の電圧波形です．入力信号がダイオードの順方向電圧以上にならないと出力電圧が現れないため，振幅が0.4Vppの時は整流波形が出力されず，2Vppの時も振幅の小さい整流波形になっています．

図4　図3の回路のシミュレーション結果
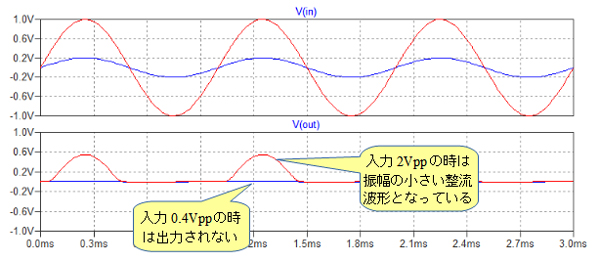
入力信号が小さい時はV(out)に整流波形が出力されない．

　この問題を解決するために考えられたのが，図5のOPアンプを使用した整流回路です．この回路は反転アンプとなっており，入力信号が負の時，出力は位相の反転した正の出力が現れます．その時のゲインは「R2/R1」で決まります．入力信号が正の時，出力はGNDレベルになります．

図5　OPアンプを使用した半波整流回路

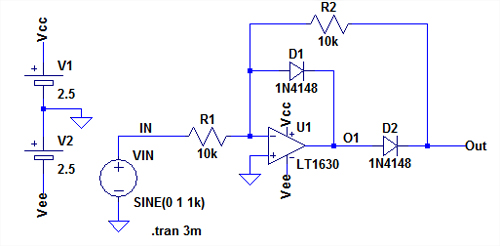
　図6は，図5のシミュレーション結果です．下段の出力信号[V(out)]は綺麗な半波整流波形になっていることがわかります．上段のV(o1)はOPアンプの出力をモニタしたものです．V(o1)はOPアンプの出力なので，入力信号が負の時は，V(out)にD2の順方向電圧を加えた電圧となっており，入力信号が正の時は，GNDからD1の順方向電圧だけ下がった電圧になります．もし，D1が無いと，入力信号が正の時にOPアンプに負帰還がかからず，V(out)に入力信号がそのままスルーして出力され綺麗な半波整流波形になりません．

図6　図5のシミュレーション結果
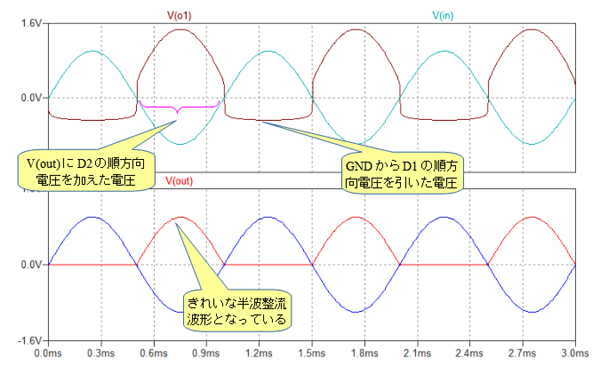
V(out)はきれいな半波整流波形となっている．

●半波整流回路から全波整流回路へ
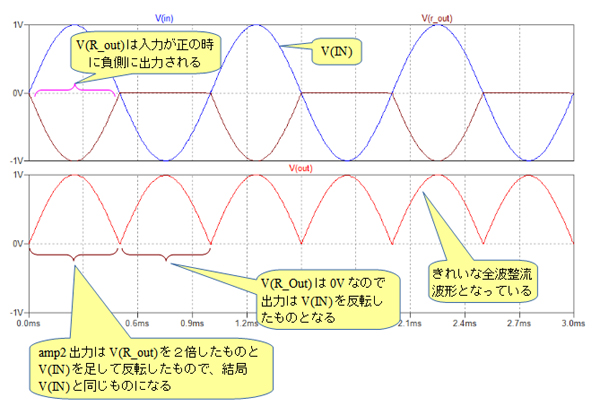
　図7は，回路(a)のシミュレーション用の回路です．amp2は，反転アンプを利用した加算回路を構成しています．ダイオードD1とD2の向きが図5とは逆になっています.これは，amp2により位相が反転してしまうため，R_outの出力を負側の半波整流波形とするためです．

図7　回路(a)のシミュレーション用回路
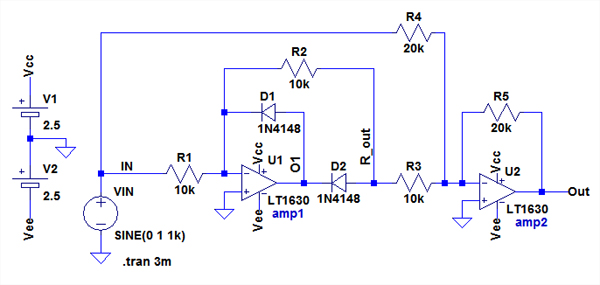
anp2による反転アンプがあるため，出力が正方向となるよう，ダイオードD1とD2の向きは図4とは逆向きにしている．

　図8は，図7のシミュレーション結果です．図8の下段のV(out)は，きれいな全波整流波形となっています．入力信号が正の時，V(R_out)はamp1により入力信号を反転した波形となります（式1）．また，V(R_out)はamp2で2倍（R5/R3=2）に増幅され，反転して出力されます．一方，V(IN)は，amp2で1倍（R5/R4=1）で増幅され，反転して出力されます．つまり，amp2の出力[V(Out)]には2倍のV(R_out)とV(IN)が加算され，反転して出力されることになります．式2からわかるように，V(Out)はV(IN)と同じ正の信号が出力されます．

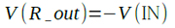・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

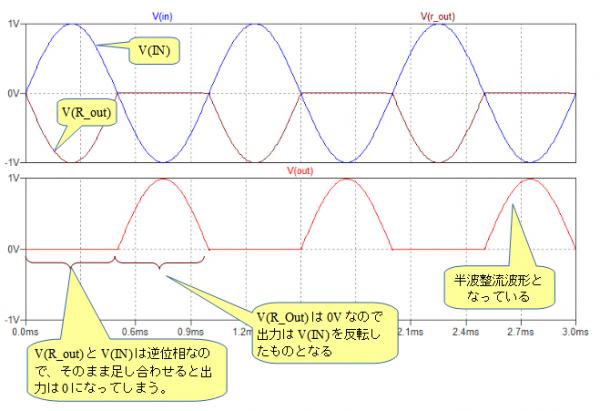
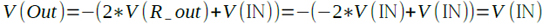・・・・・(2)

　次に，入力信号が負の時，V(R_out)はGNDレベルとなっています．この時amp2出力[V(out)]にはR4に加えられた入力信号V(IN)を反転した波形が出力されます．このようにしてV(out)は全波整流された波形になります．

図8　図7のシミュレーション結果
出力はきれいな全波整流波形となっている．

●ゲイン1で加算すると半波整流に
　図9は，回路(b)のシミュレーション用の回路です．図10は，そのシミュレーション結果です．V(out)は，半波整流波形となっています．入力信号が正の時は，V(IN)とV(R_out)が逆位相で同じ振幅のためamp2で加算すると0になってしまいます(式3）．入力信号が負の時は図8と同様のV(IN)を反転したものがV(Out)に出力されます．

図9　回路(b)シミュレーション用の回路
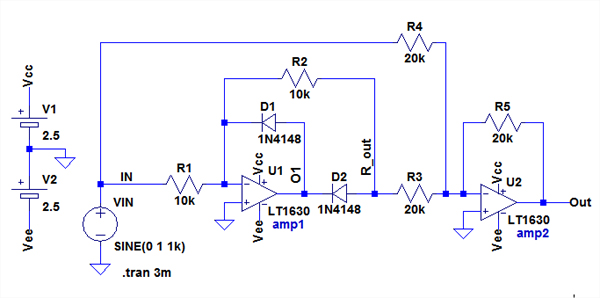
図8との違いはR3が20kΩになっている．

図10　回路(b)のシミュレーション結果
出力は全波整流波形では無く，半波整流波形となっている．

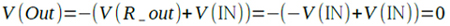・・・・・・・・・・・・(3)

　この回路形式で全波整流波形を得るには，入力信号と2倍の振幅で逆位相の半波整流波形を加算する必要があります．R3が20kΩでも，R2を20kΩとしてV(R_out)の振幅を2倍にすればV(Out)を全波整流波形とすることができます．ただし，振幅が2倍になることから，入力信号が大きい時に半波整流波形がクリップ（飽和）してしまう点に注意が必要となります．

●回路が簡単な単電源の全波整流回路
　回路(a)と(b)は，OPアンプを±電源（両電源）で使用した回路でしたが，OPアンプを単電源で利用して，GND基準の全波整流出力を得たいという用途も，いろいろな回路で考えられます．最後にその中の一つを紹介します．OPアンプを単電源で利用する場合，OPアンプは入出力レール・トゥ・レールのものが必須となります．また，大きな入力信号が扱えない(0.6Vpp程度まで)ことや周波数が高いと上手く動作しない，精度が低いといった欠点があります．しかし，回路は比較的簡単になります．
　図11が単電源で動作する全波整流回路です．入力信号は，回路(a)と(b)の1/10の0.2Vppの正弦波で，amp2で10倍にしています．回路の初段は反転アンプで，入力信号が負の時はV(IN)を反転した出力がR_outに出力されます．入力信号が正の時はOPアンプは負電圧が出力できないため飽和し，V(IN)がそのままR_outに出力されます．OPアンプは0Vを出力していますが，D1があるため，V(R_out)はV(IN)と同じになります．このようにしてV(R_out)に全波整流波形が出力されます．amp2はゲイン10倍の非反転アンプです．

図11　単電源で動作する全波整流回路
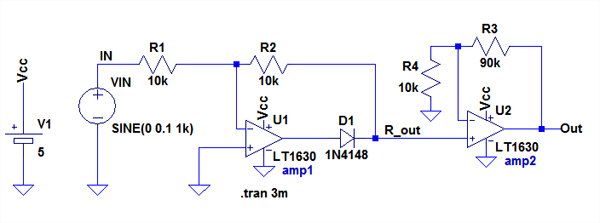
入出力レール・トゥ・レールのOPアンプが必須で大きな入力電圧は扱えない．

　図12が図11のシミュレーション結果です．入力信号が正の時と負の時で出力振幅が，OPアンプが飽和することにより，多少異なってしまっていますが，一応GND基準の全波整流波形が得られています．

図12　図11のシミュレーション結果
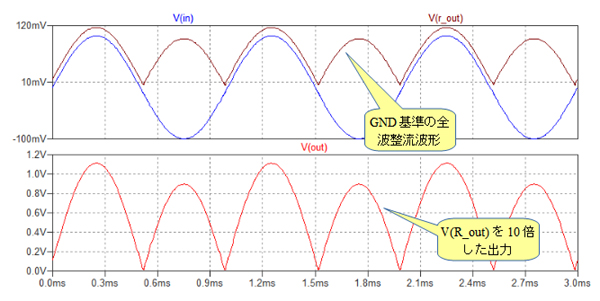
入力信号の正負で出力振幅が異なってしまっているがGND基準の全波整流波形が得られている．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice034.zip

●データ・ファイル内容
diode_recti.asc：図3の回路
Half-wave_recti.asc：図5の回路
Full-wave_recti_A.asc：図7の回路
Full-wave_recti_B.asc：図9の回路
Full-wave_recti_2.asc：図11の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください