正しい波形が観察できるプローブの回路はどっち？
図1の回路(a)と(b)は，10:1のパッシブ・プローブをオシロスコープに接続した状態の簡易等価回路です．回路(a)のコンデンサ（C1）は10pFで，回路(b)のコンデンサ（C1）は9pFとなっています．このプローブで2kHz，1VPPの矩形波を観察した時，正しい波形が観察できるのはどちらでしょう？
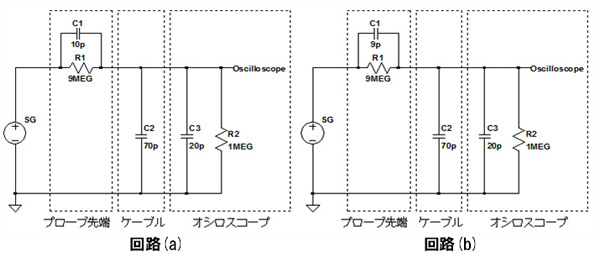
回路(a)のC1は10pFで，回路(b)のC1は9pFとなっている
回路(a)
10:1のパッシブ・プローブは，どんな周波数でも入力信号を1/10にしてオシロスコープに伝える必要があります．そのためには，図1において，C1/(C1+C2+C3)=R2/(R1+R2)が成り立つような定数となっている必要があります．
回路(b)はC1（9pF）が適正値より小さく，高い周波数で分圧比が大きくなり，高域が減衰する特性になるため，肩の丸まった波形になってしまいます．
回路(a)のC1（10pF）は，C1/(C1+C2+C3)=R2/(R1+R2)が成り立つ適切な値になっているため，周波数特性はフラットになり，プローブ先端の入力と相似した波形がオシロスコープの入力に加わります．つまり，正しい波形が観察できるのは回路(a)のプローブです．
●10:1プローブを使う理由
オシロスコープを使って信号を観察する時に使用されるパッシブ・プローブは10:1のものがよく使用されます．これは観察すべき回路への影響を小さくするために，プローブの入力インピーダンスをできるだけ大きくするためです．10:1のアッテネータ（減衰器）を挿入することで，プローブの入力抵抗はオシロスコープの入力抵抗の10倍になり，入力容量は，オシロスコープの入力容量にケーブル容量を加えたものの1/10の容量にすることができます．ただし，プローブについている周波数特性調整用トリマの調整を怠ると，正しい波形観察ができないため，測定前にかならず調整する必要があります．
●周波数特性がフラットになる抵抗とコンデンサの値を求める
図1でR2はオシロスコープの入力抵抗，C3はオシロスコープの入力容量，C2はケーブルの容量です．このように，10:1のパッシブ・プローブ回路は，C1，R1とR2，C3，C2とで分圧回路を構成しており，どんな周波数でも同じ分圧比（周波数特性がフラット）になっている必要があります．これらの素子の値をどのように選べば周波数特性がフラットになるかを考えてみます．まず，直流での分圧比KDCはR1，R2だけで決まり，式1になります．
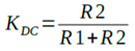・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また，R1とR2のインピーダンスが無視できるような高い周波数での分圧比はC1，C2，C3で決まり，式2のようになります．
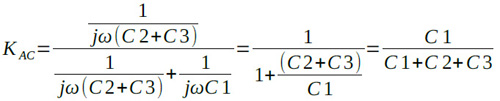・・・・・・・・・(2)
ここでKDC=KACとなるように定数を設定すれば，直流でも高い周波数でも分圧比は同じになり，分圧比の周波数特性をフラットにすることができます．つまり，周波数特性がフラットになる条件は式3になります．
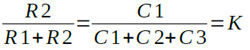・・・・・・・・・・・・・・・・・・・・・・・・・(3)
図1において，R1=9MΩ，R2=1MΩですから，式3より，Kは0.1となります．式3を変形してC1について解いたものが，式4になります．数値を代入すると，C1は10pFにすればよいことが分かります．
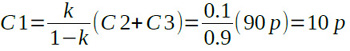・・・・・・・・・・・・・・・・・・・(4)
この時プローブの入力抵抗RINはR1とR2が直列になるので，式5のように10MΩとなり，入力容量CINはC1と(C2+C3)が直列になるので，式6のように9pFとなります．
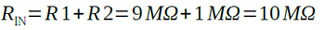・・・・・・・・・・・・・・・・・・・・(5)
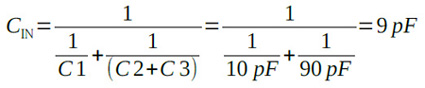・・・・・・・・・・・・・・(6)
●図1の波形をシミュレーションしてみる
それでは，図1の回路の波形をシミュレーションしてみます．図2は，比較しやすいように，回路(a)と(b)を一つにまとめた，シミュレーション用の回路図です．図3がそのシミュレーション結果です．回路(a)の出力V(a)は綺麗な矩形波になっていますが，回路(b)の出力V(b)は角の丸まった波形となっています．
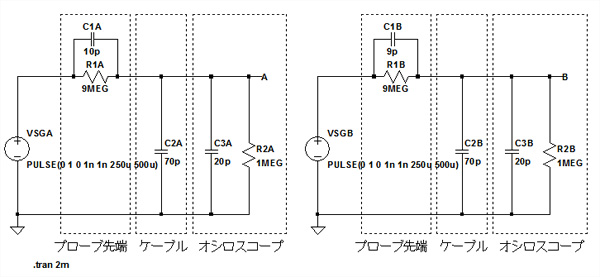
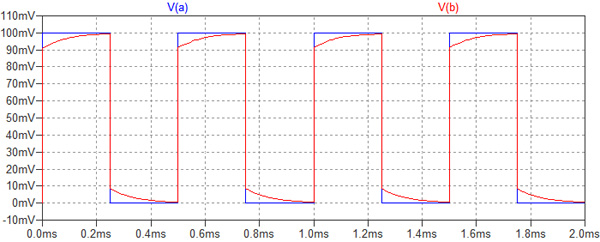
回路(a)の出力V(a)は綺麗な矩形波．回路(b)の出力V(b)は角の丸まった波形
●C1の値を変化させてシミュレーションしてみる
次にC1を周波数調整用トリマとした場合を想定し，C1を7pFから13pFまで変えて，2kHzの波形と周波数特性がどのように変化するかを確認してみます．C1の値は，変数を使用するため，{C}と入力します．次に「.step param C 7p 13p 1p」としてCを7pFから13pFまで1pFおきに変化させて解析を行います．図4が過渡解析用の回路図で，図5がそのシミュレーション結果です．
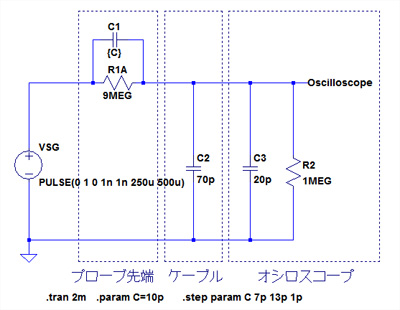
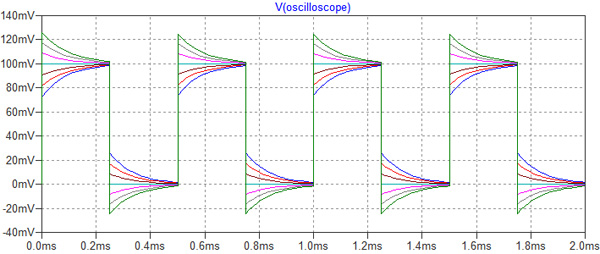
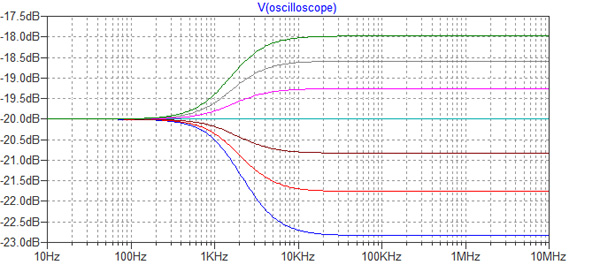
図6が周波数特性解析用の回路図で，図7はそのシミュレーション結果になります．C1を変化させることで周波数特性が変化し，出力波形がかなり変化することがわかります．
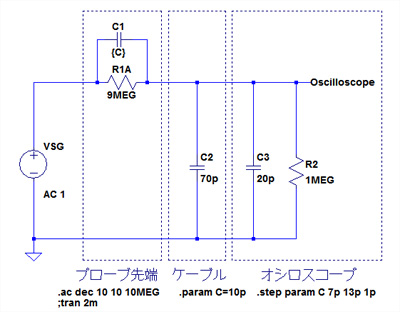
プローブによっては，周波数特性調整用のトリマがプローブ先端ではなく，オシロスコープとの接続コネクタ部分についているものもよくあります．このようなプローブでは図8のように，C1は固定コンデンサとし，オシロスコープの入力側に周波数特性調整用のトリマ・コンデンサ（C4）を接続しています．
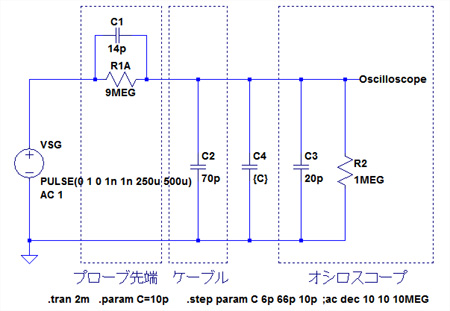
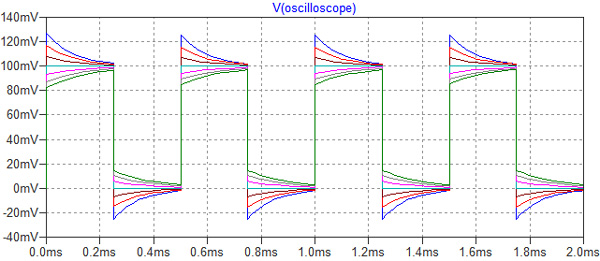
図9は，C4を6pから66pまで10pおきに変化させた時の出力波形のシミュレーション結果です．図5と同様に波形が変化していることがわかります．
●ケーブルの抵抗が波形に与える影響をシミュレーション
ここまでは，ケーブル部分を単純なコンデンサとした等価回路でシミュレーションしてきました．実はパッシブ・プローブに使用されているケーブルは，アンテナ配線に使用される同軸ケーブルとは異なる，特殊なものが使われています．同軸ケーブルを使用して信号を伝送する場合は，入出力インピーダンスをケーブルの特性インピーダンスに合わせる必要があります．しかしながら，パッシブ・プローブは，入力インピーダンスをできるだけ高くする必要があり，インピーダンスを合わせることができません．そのような状況で通常の同軸ケーブルを使用すると，信号の反射が発生し，正確な波形観察ができなくなってしまいます．
そのため，パッシブ・プローブでは芯線に故意に抵抗の大きな線材を使用することで，信号の反射を防ぐような工夫をしています．LTspiceにはこのようなシミュレーションに使用可能な「Lossy transmission line」が用意されているので，これを使用して芯線の抵抗値による波形の違いをシミュレーションしてみます．
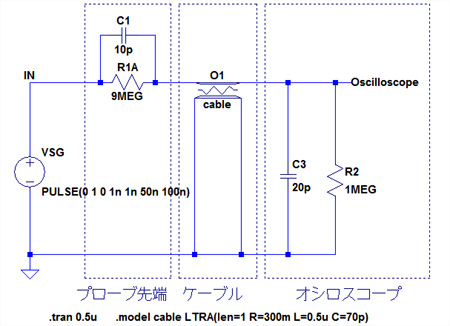
図10はケーブル部分を「Lossy transmission line」に置き換えたものです．LTspiceでは「ltline」という名前で登録されており，シンボル選択画面から選択することが可能です．また，「ltline」を使用する場合はモデルを定義する必要があります．ここでは「cable」というモデルを定義しています．「.model cable LTRA(len=1 R=300 L=0.5u C=70p)」各パラメータの意味は次のようになっています．
R＝単位長さあたりの抵抗値
L＝単位長さあたりのインダクタンス
C＝単位長さあたりのキャパシタンス
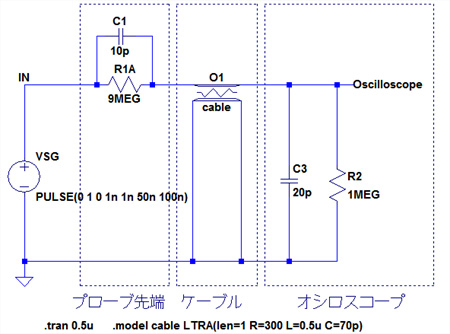
今回ここで定義した数値は実在のケーブルのものではなく，シミュレーション用に設定したものです．単位長さあたりの抵抗値は300Ωとしています．信号として10MHzの矩形波を入力してトランジェント解析を行った結果が，図11になります．出力波形は，ほぼ矩形波となっています．
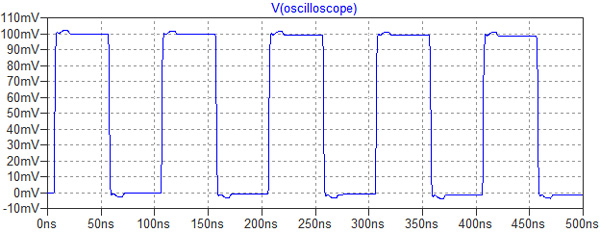
図12は芯線の抵抗が小さい時をシミュレーションするための回路で，R=300mΩとしています．図13がそのシミュレーション結果です．比較のために入力波形も表示していますが，出力波形は反射の影響がひどく，入力波形とはまったく異なる波形になってしまっています．
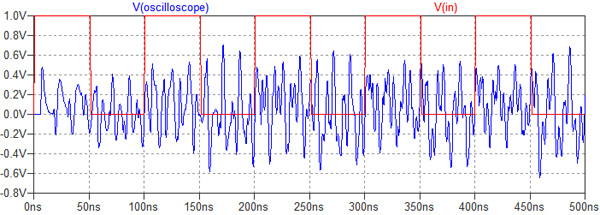
普段何気なく使っているパッシブ・プローブですが，正確な波形を観察するために，色々な工夫が盛り込まれていることがわかります．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice024.zip
●データ・ファイル内容
probe_A_B_Tran.asc：図2の回路
probe_Tran_step.asc：図4の回路
probe_Ac_step.asc：図6の回路
probe2_Tran_step.asc：図8の回路
probe_LTLINE.asc：図10の回路
probe_LTLINE_R300m.asc：図12の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
