入力と同時に積分を開始する回路はどっち?

図1は,直流オープン・ループ・ゲインが80dB, 1st poleが10HzのOPアンプを用いた積分器です.回路(a)は,反転端子と出力端子の間がコンデンサ(C1)のみとなります.回路(b)は,抵抗と直列のコンデンサ(R3,C2)で構成しています.この回路(a)と(b)で,ステップ入力の立ち上がりと同時に積分を開始する回路はどちらでしょうか?OPアンプは,直流オープン・ループ・ゲインや周波数特性以外は理想とします.
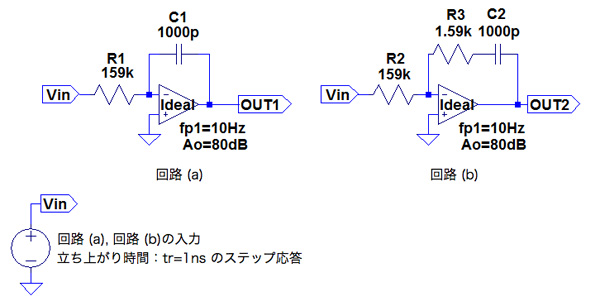
回路(a)の反転端子と出力端子間はC1のコンデンサのみで構成した積分器
回路(b)の反転端子と出力端子間はC2のコンデンサとR3の抵抗で構成した積分器
回路(b)
図2は,回路(a)と(b)のステップ応答を示したグラフです.回路(a)の伝達関数は,理想積分器の項「-1/sCR」と1次遅れ系の項「1/(1+sτ/Ao)」の積です.その高周波応答は,理想積分の応答から1次遅れ系の分だけ遅れた青線のステップ応答となります.ここで,τは,1st poleの10Hzから求まる値(1/2πfp1)で,Aoは,OPアンプの直流オープン・ループ・ゲインです.回路(b)は,理想積分器の項と1次遅れ系の項を抵抗(R3)でゼロ補償した積となり赤線のステップ応答になります.
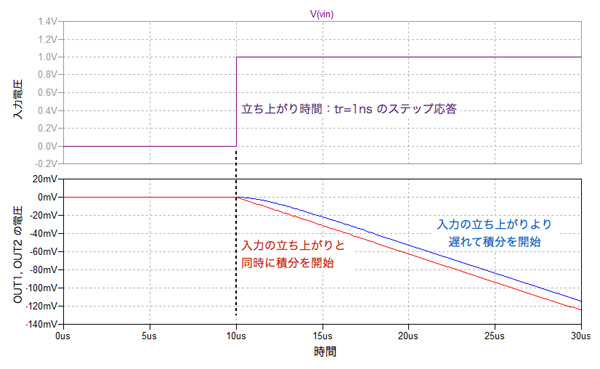
回路(a)が青線のステップ応答,回路(b)が赤線のステップ応答
●アナログ・コンピュータで使用された積分器
積分器は,入力信号の積分に比例した出力信号を得られる回路です.その用途は広くOPアンプの歴史を振り返ればアナログ・コンピュータの積分器として使われました.また身近な回路例では,アクティブ・フィルタやサンプル・ホールド回路の中でも使われています.積分器の誤差はOPアンプの入力オフセット電圧,入力オフセット電流,入力バイアス電流等によるものがあります.ここでは,OPアンプのオープン・ループ・ゲインとその周波数特性による積分器の高周波応答の誤差について考えていきます.
積分器は,図3に示すブロック図で表せば入力信号の積分に比例した出力を得るものです.時間軸は式1,周波数軸は式2となり式中のKは積分器の比例定数です.式1と式2の右辺第二項は初期値です.通常は初期値を0として扱うのが一般的です.
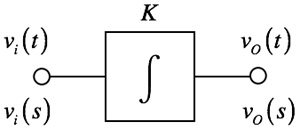
入力信号の積分に比例した出力を得る
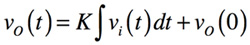 ・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・(1)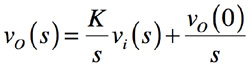 ・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・(2)OPアンプを使った積分器は図4に示すもので,反転端子と出力端子間の帰還容量を使った回路です.図4のクローズ・ループ伝達関数は式3であり,「1<<A(s)β(s)」が成り立てば「K=-1/CR」の積分比例定数を持つ積分器となります.
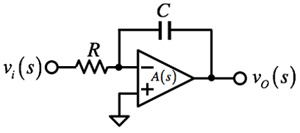
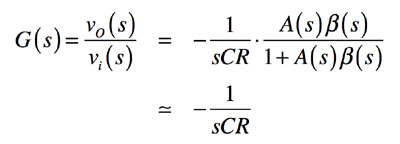 ・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・(3)
●OPアンプの周波数特性が低周波に1st poleを持つ1次遅れ系の場合を調べる
図4は,回路(a)と同じであり,使われているOPアンプのオープン・ループ・ゲイン周波数特性が低周波に1st poleを持つ場合の積分器伝達関数を計算し,それを逆ラプラス変換して回路(a)の時間軸での高周波応答を調べます.時間軸での高周波応答は高い周波数成分まで含んだステップ応答を用います.
OPアンプのオープン・ループ・ゲインは,直流利得を「Ao」,1st poleを「-1/τ」として,
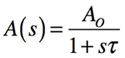 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
また,図4の帰還率は,
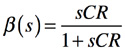 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
式3のA(s)とβ(s)へ式4,式5を代入して整理すると式6が得られます.
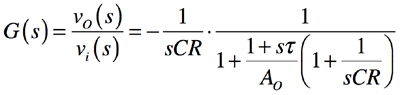 ・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・(6)
高周波応答を考えるので式7の近似を用います.またOPアンプの直流オープン・ループ・ゲインが1より十分大きいとすれば式8の近似もできます.
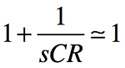 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
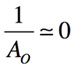 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
式6へ式7と式8の近似を用いると,
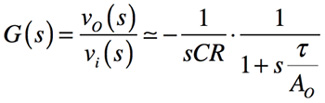 ・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・(9)
式9は理想積分器の項「-1/sCR」と1次遅れ系の項「1/(1+sτ/Ao)」の積であることから,図5に示す縦続接続した回路と等価であることがわかります.よって回路(a)の高周波応答は理想積分の応答から図5の1次遅れ系の項だけ遅れ,そのステップ応答はステップ入力の立ち上がり時間より遅れて積分を開始します.
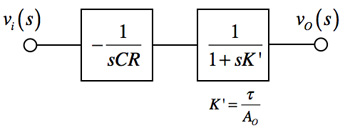
1/(1+sK’)の逆ラプラス変換をし,時間軸での出力端子の遅れ時間を計算すると,
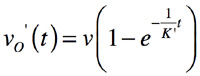 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
ここで,
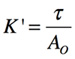 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
このように式11で求まる値だけ時間軸での遅れが発生します.また式12を用いて高周波領域の利得が1となる周波数fTとK’の関係を調べると
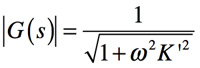 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
「1<<ω2K‘2」であること,また,「1st pole=10Hz」と「Ao=80dB」の1次遅れ系の利得「|G(s)|=1」となる周波数は,「fT=100kHz」であることから,
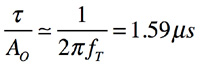 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(13)
以上より,回路(a)のステップ応答は積分器の抵抗とコンデンに関係なくOPアンプのオープン・ループ・ゲインと1st pole周波数に起因する遅れがあり,理想積分から1.59μs遅れた積分出力になります.
●回路(a)の遅れを補償する回路(b)を計算する
回路(b)の積分器伝達関数は上記と同じように近似を用いて式を整理すると,
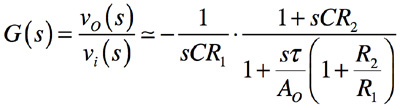 ・・・・・・・・・・・・・・(14)
・・・・・・・・・・・・・・(14)
式14の右辺分子にある「1+sCR2」の「R2」をその分母と同じになるよう式15のように選べば分母と分子が打ち消され理想積分の-1/sCR1になると期待できます.
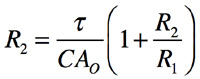 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(15)
「R2」で整理し,
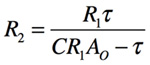 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(16)
τは低周波(10Hz)にある1st poleであり,「τ=1/(2π×10Hz) = 0.0159s」です.また「CR1Ao>>τ」と近似できますので,高周波応答を補償する抵抗R2は式17が目安となり,
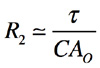 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(17)
「R2=1.59kΩ」が導き出されます.
●LTspiceで回路(a)と(b)のステップ応答を確かめる
図6は回路(a)と(b)の高周波応答を調べる回路です.比較のために直流オープン・ループ・ゲインが80dBで無限大周波数まで一定(周波数による減衰がない)の理想積分器[回路(c)]も用意しました.
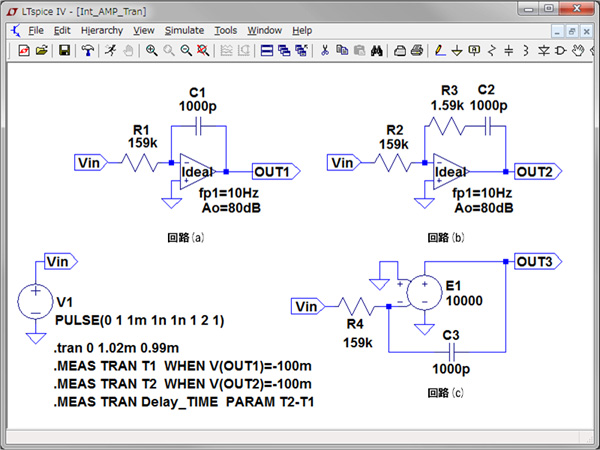
回路(c)はオープン・ループ・ゲイン80dBで周波数特性を持たないOPアンプで構成した理想積分器
図7がその結果です.回路(a)の出力はステップ入力の立ち上がりから遅れて積分出力しています.回路(b)はその遅れ時間を補償した回路であり,ステップ入力の立ち上がりと同時に積分出力をしており期待通りの結果です.また,理想積分回路の回路(c)の出力は,回路(b)と重なっており,回路(b)は理想積分器と同じ働きをしていることが分かります.
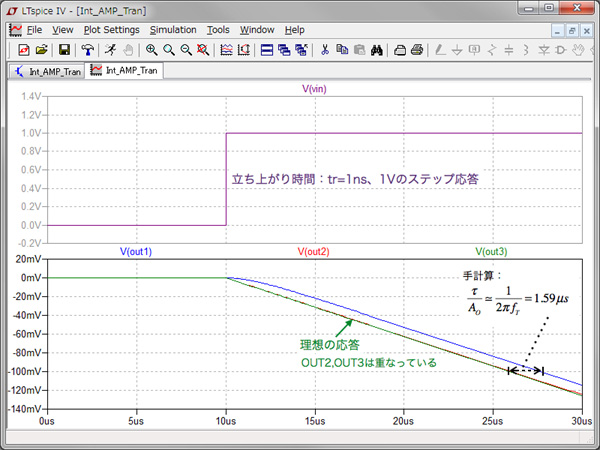
回路(b)は理想積分回路の回路(c)と重なっている
カーソル機能で遅れ時間を測るが大変なので,「.MEAS」コマンドを用いて回路の積分器の出力が-100mVになる時間を探し出し,その時間差を1回のシミュレーションで得られるようにしました.
積分器の出力が-100mVになる時間を探す 「.MEAS」コマンドはWHENを用いて任意の変数へその時間を格納します.OUT1を例にとると次のコマンドになります.
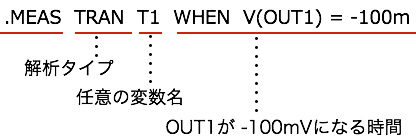
上記で探し出した積分器の出力が-100mVになるOUT1とOUT2の時間は変数T1とT2に格納されています.「.MEAS」コマンドのPARAMを用いて変数間の減算をおこない,それを変数「Delay_TIME」へ次のように格納します.
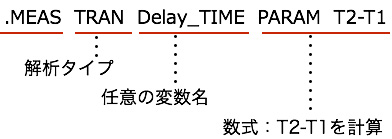
「.MEAS」コマンドの結果はログ・ファイルに記録されます.ログ・ファイルを見るときはメニューバーの「View > SPICE Error Log」または,ショートカット・キーの「Ctrl+L」でログ・ファルのウィンドが現れます.
ログ・ファイルには,次が記載されています.
t2: v(out2)=-100m AT 2.60627e-005
delay_time: t2-t1=-1.5728e-006
これより回路(a)と回路(b)の高周波応答の遅れ(時間差)は1.57μsであり,式13の手計算で求めた値と同等な結果であることが確かめられました.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice019.zip
●データ・ファイル内容
Ideal_OP.asc:OPアンプの回路
Ideal_OP.asy:OPアンプのシンボル
Int_AMP_Tran.asc:図6の回路
※ファイルは同じフォルダに保存して,フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs










