出力電圧のばらつきが少なくなる回路はどっち?

図1の回路(a)と(b)ともに抵抗分圧により,電源電圧の1/2の電圧を出力する回路です.回路(a)は10KΩの抵抗2本で分圧回路を構成し,回路(b)は2kΩの抵抗を5本直列にしたものを2組使用して分圧回路を構成しています.この回路の電源電圧は10Vで,出力電圧のスペックは5V±2.5%とします.
どちらの回路にも,一様分布で±5%のばらつきのある抵抗を使用し,1000台ずつ製作した場合,不良率が低いのはどちらの回路でしょうか?ただし,電源電圧のばらつきや,OPアンプのオフセット電圧のばらつきは無いものとして考えます.
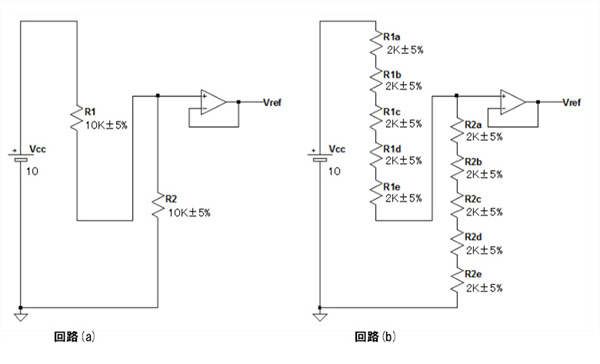
回路(a)は10KΩの抵抗2本で構成し,回路(b)は2kΩの抵抗を5本直列を2組,合計10本で構成している
回路(b)
ばらつきのある抵抗を複数本直列に接続すると,合成抵抗値のばらつきの分布を改善することができます.そのため,回路(b)の2kΩの抵抗5本を2組使用した分圧回路のほうが,出力電圧のばらつきが小さく,5V±2.5%のスペックで選別した時の不良品率が小さくなります.
●誤差のワースト値と誤差の分布
今回のように,ばらつきのある部品を使用して製品を作る場合,特性の分布と特性のワースト・ケースの値は分けて考える必要があります.
▼誤差のワースト値
回路(b)の5本直列にしたものを簡単に解説するために,まず,±5%の誤差をもったRΩの抵抗を2本直列にした場合について考えてみます.誤差のワースト値ですが,当然2本の抵抗がともに+5%もしくは-5%の時に誤差が最大になります.抵抗が大きくなる方向で考えると,合成抵抗RTは式1となります.
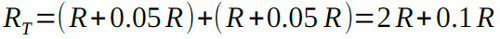 ・・・・・・・・(1)
・・・・・・・・(1)
この合成抵抗の誤差は,式2となり,もとの抵抗と同じ5%の誤差,ということになります.
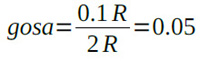 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
▼誤差の分布
次は,合成抵抗値の分布について考えてみます.もし,一方の抵抗が+5%で,もう一方の抵抗が-5%だった場合,合成抵抗は式3となり,誤差は打ち消されてしまいます.
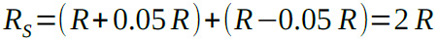 ・・・・・・・・・・・・(3)
・・・・・・・・・・・・(3)
このように誤差が打ち消される組み合わせが発生するため,個々の抵抗の誤差が一様分布だったとしても,合成抵抗はセンタ値付近の値の発生頻度が多い分布となります.直列に接続する抵抗を多くすれば,よりセンタ値付近の発生頻度が多く,分布の幅は狭くなっていきます.
統計的な考え方が必要になるため,少し分かり難いのですが,どのように狭くなっていくかを計算してみます.まず,抵抗値RΩの抵抗において,最大誤差が±ΔRで分布の形は一様分布となる抵抗で考えます.この抵抗の標準偏差はΔR/√3となりますが,ここではこれをσとします.標準偏差がσなので,分散値はこれを二乗してσ2となります.この抵抗をN個直列にすると抵抗値はN*Rになり,分散値はN*σ2となります.合成抵抗の標準偏差をσTとすると,式4となります.
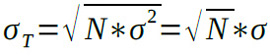 ・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・(4)
一個あたりの抵抗に換算した標準偏差をσSとすると式5となります.
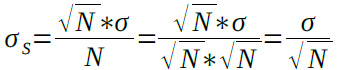 ・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・(5)
このように,合成抵抗の標準偏差(ばらつきの度合い)は元の抵抗の標準偏差の「直列個数の平方根分 の1」になり,分布がせまくなります.
●LTSpiceで抵抗の分布を検証する
LTSpiceには,部品のばらつきをシミュレーションする時に便利な,モンテカルロ解析という機能があるので,これを使って検証していきます.
図2は,抵抗値の分布をシミュレーションするための回路です.10kΩで±5%の一様分布の誤差が発生する抵抗に,1mAの電流を流しています.このため,出力電圧は10V±0.5Vとなるはずです.
tolという変数に0.05(精度5%)という値を代入し,R1の抵抗値を{mc(10k,tol)}と指定して一様分布な誤差を発生させます.
「.step param X 1 1000 1 」の中のXは,ダミー変数で,モンテカルロ解析の回数を指定します.
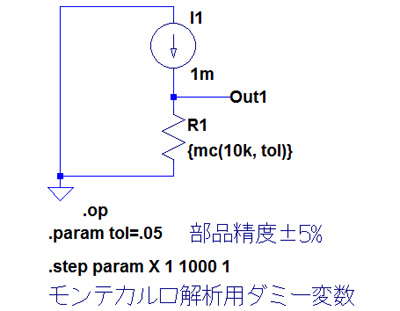
0kΩで±5%の一様分布の誤差が発生する抵抗に,1mAの電流を流す
図3がシミュレーション結果です.横軸は試行回数で,縦軸はV(out1)/I(I1)をプロットし,抵抗値として表示させていいます.抵抗値は10K±0.5KΩの間でほぼ一様に分布していることがわかります.
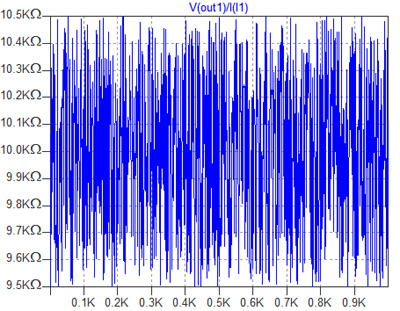
10K±0.5KΩの間で一様に分布
図4は2kΩの抵抗を5本直列に接続した場合の抵抗値の分布を調べるための回路です.図3と同様なシミュレーションを行った結果が図5になります.縦軸のレンジは図3と揃えてありますが,抵抗値の分布が図3に比べて狭くなっていることがわかります.
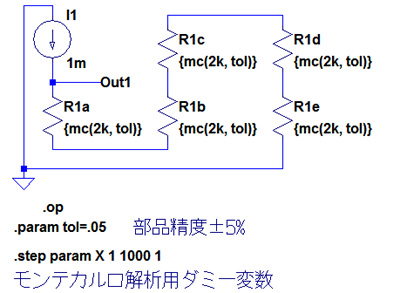
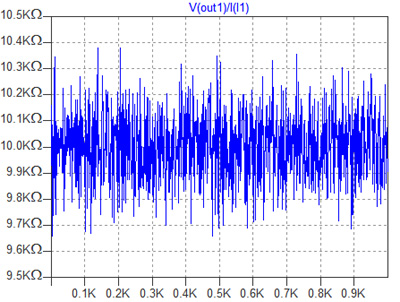
抵抗値の分布が狭くなっている
このように抵抗を直列に多数接続することによって,元の抵抗よりも抵抗の分布の幅を狭くすることができます.抵抗の並列接続でも同様な効果が得られます.図6は50kΩの抵抗5本を並列接続した時の抵抗値の分布を調べるための回路です.図7がそのシミュレーション結果です.図5と同様に抵抗値の分布が狭くなっています.
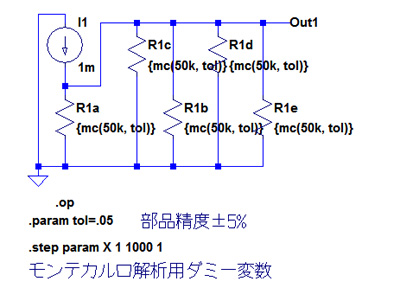
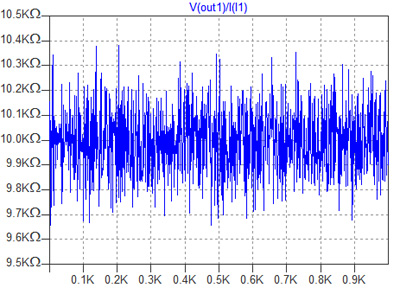
直列接続と同様に抵抗値の分布が狭い
LTSpiceの波形ビューアでもおおまかな分布の形はわかりますが,表計算ソフトで抵抗値の度数分布グラフを作成すると,よりわかり易くなります.データを表計算ソフトに取り込むために,波形ビューアをアクティブにして[File][Export]とします.すると,拡張子が「TXT」のファイルが出力されます.このファイルの拡張子をCSVに変更し,タブ区切りCSVファイルとして表計算ソフトに取り込みます.図8は,このようにして作成した抵抗値のヒストグラムデータです.抵抗値の分布の違いがよくわかると思います.
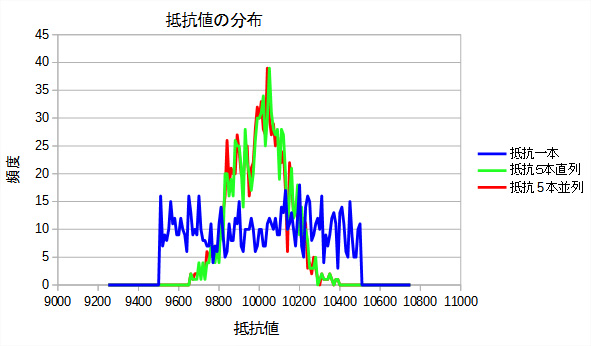
抵抗値の分布の違いがよくわかる
●分圧回路のばらつきのワースト・ケースを考える
分圧回路のばらつきについて考えてみます.こちらも電圧値のワースト・ケースと分布は別々に考える必要があります.まず,図1の回路(a)の出力電圧の値が,センタ値と一番ずれるのは,それぞれの抵抗が逆方向にばらついた時です.例えば,R1が+5%,R2が-5%の時のことを考えてみます.
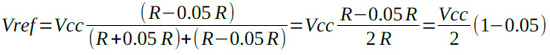 ・・・・・(6)
・・・・・(6)
式6のように,センタ値であるVcc/2から5%低い電圧になります.R1が+5%,R2が-5%ずれると,Vrefは合計で10%ずれると勘違いしますが,ずれるのは5%です.
●回路(a)のばらつきの分布を考える
回路(a)の分圧回路のばらつきについて考えてみます.分圧回路でも抵抗の直列接続同様,誤差が打ち消されるばらつきの組み合わせが存在します.例えば,R1とR2がともに+5%になった場合,分圧値はVcc/2となり,誤差が発生しません.
それでは,どのような分布になるか,さっそくシミュレーションを行ってみます.図9がシミュレーション用の回路で,図10がシミュレーション結果となります.回路(a)と(b)にあったOPアンプは結果には影響しないので省略してあります.出力電圧は5V±5%(4.75Vから5.25Vの間)に分布するはずで,シミュレーション結果もそのようになっています.図10を見ると,一様分布では無く,センタ付近の個数が多いように見えますが,分かり難いので,これも表計算ソフトでヒストグラムを書かせて確認します.
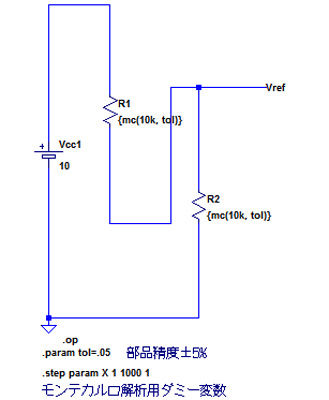
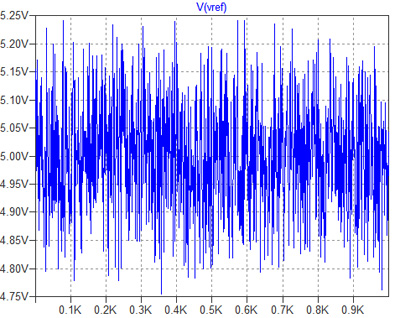
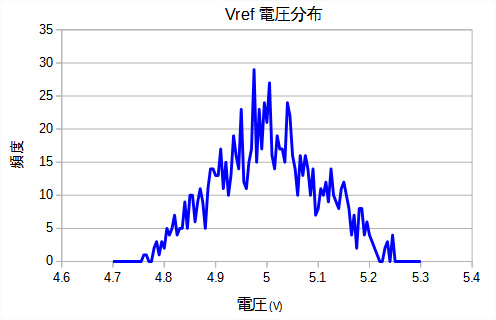
図11がそのヒストグラムです.一様分布の抵抗を使用していても,Vrefの電圧分布は一様分布ではなく,三角形の形をしていることが確認できます. 5V±2.5%(4.875V~5.125V)というスペックからはずれて不良となるのは1000回中234回でした.
つまり,回路(a)の不良率は23.4%ということになります.±5%精度の抵抗を使用しているので,±2.5%というスペックでは,半数の50%が不良になってしまいそうですが,そうならないところが面白いところです.
●回路(b)のばらつきをシミュレーションする
最後に,回路(b)の回路をシミュレーションしてみます.図12がシミュレーション用の回路です.図13がそのシミュレーション結果ですが,図10の結果と比べ,明らかに分布の幅が狭くなっていることがわかります.
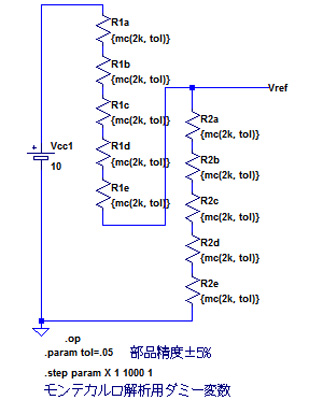
5本直列分圧シミュレーション回路
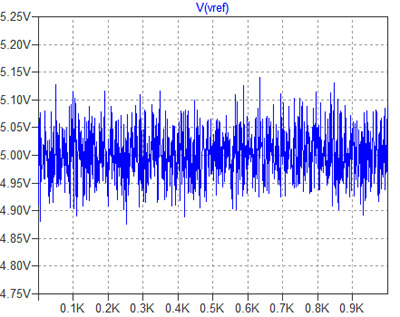
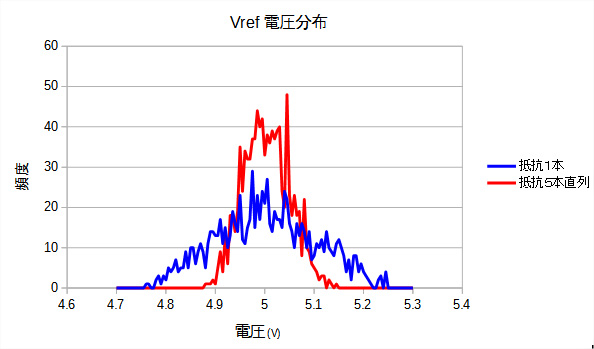
図14は,図13のシミュレーション結果のヒストグラムを,図11のヒストグラムに重ね書きしたものです.5V±2.5%(4.875V~5.125V)というスペックからはずれて不良となるのは1000回中4回でした.つまり,回路(b)の不良率は,わずか0.4%ということになります.回路(a)の不良率は23.4%でしたから,今回の問題の回答は,「回路(b)のほうが不良率が低い」ということになります.
このように,複数の抵抗を組み合わせることで,ばらつきの分布を改善することが可能です.ただし,分布を狭くすることは可能ですが,ワースト・ケースの値が発生する確率が0になるわけではない点に注意が必要です.
今回は抵抗分圧回路で説明しましたが,この手法をアンプのNF抵抗などに応用して,アンプのゲインのばらつきを改善することなどが可能です.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice018.zip
●データ・ファイル内容
MonteCarlo_1R_J.asc:図2の回路
MonteCarlo_5R_S_J.asc:図4の回路
MonteCarlo_5R_P_J.asc:図6の回路
V_Div_A.asc:図9の回路
V_Div_B.asc:図12の回路
※ファイルは同じフォルダに保存して,フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs










