雑音が少ない1次ロー・パス・フィルタはどっち?

図1の回路(a)と(b) は,抵抗とコンデンサで構成した1次ロー・パス・フィルタ(Low Pass Filter:LPF)です.カットオフ周波数は,回路(a)は3.18kHzで,回路(b)は5kHzとなります.この場合,雑音が少ない回路はどちらでしょうか?
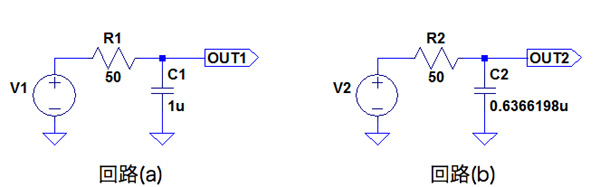
回路(a)と(b)の違いは,コンデンサとカットオフ周波数
回路(a)
1次LPFの雑音帯域幅の求め方は,「カットオフ周波数×π/2」です.回路(a)のカットオフ周波数(3.183kHz)とπ/2の積は5kHzです.また,回路(b)のカットオフ周波数(5kHz)とπ/2の積は約7.854kHzとなります.回路(a)と(b)の出力雑音は「抵抗の熱雑音×雑音帯域幅」です.抵抗R1とR2が同じ値ならば,抵抗の熱雑音も同じ値ですので,雑音帯域幅が狭い回路(a)のほうが出力雑音が少なくなります.
●雑音帯域幅はカットオフ周波数と異なる
図2は,回路(a)の雑音帯域幅(Δf)について解説しています.雑音帯域幅は,電力ゲイン周波数特性を積分し,その電力ゲインの最大値で除算した値です.これは,電力ゲイン周波数特性を積分して得た面積と,「電力ゲインの最大値×雑音帯域幅」の長方形の面積を等しくする値となります.1次LPFのカットオフ周波数(fc)は,「fc=1/2πCR」で求めます.時折り,雑音帯域幅とカットオフ周波数を混同される場合がありますが,雑音帯域幅とカットオフ周波数は異なります.
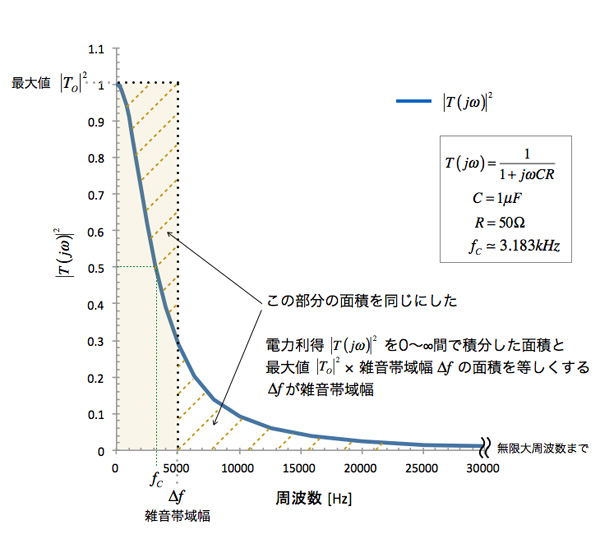
雑音帯域幅(Δf)はカットオフ周波数(fc)と異なる
●雑音帯域幅を計算で導く
式1は,雑音帯域幅をΔf, 電力ゲインの最大値をG0, 電力ゲイン周波数特性をG(f)として,周波数特性を無限大周波数まで積分した面積を四角形の一辺であるG0で除算しました.
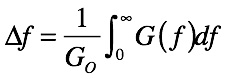 ・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
電力ゲインは電圧ゲインの2乗であることから,
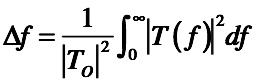 ・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・(2)
式2は電圧ゲインの周波数特性からΔfを求める計算です.
ここで図1の抵抗とコンデンサを用いた1次LPFの伝達関数は,
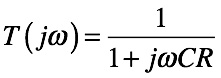 ・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3と式2より,無限大周波数まで積分した面積と,四角形の一辺となる|T0|2で除算すれば雑音帯域幅Δfが求まり,式4が導きだされます.
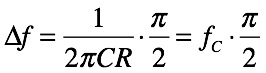 ・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・(4)
式4は,抵抗とコンデンサの1次LPFのカットオフ周波数(fc=1/2πCR)より高い周波数側に雑音帯域幅はあり,その値はカットオフ周波数にπ/2を乗算した周波数が1次LPFの雑音帯域幅であることが分かります.
●雑音帯域幅を使い1次LPFの熱雑音を調べる
回路(a)と(b)のリアクタンス分は,雑音を発生しない(ここではコンデンサ)ため雑音源になるのは抵抗の熱雑音です.図3のように抵抗の熱雑音を1次LPFの外に出し,雑音のない抵抗とコンデンサを使った1次LPFとして考えます.
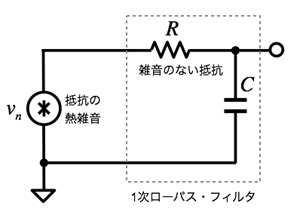
雑音のない抵抗とコンデンサを使った1次LPFとして考える
式5に示す抵抗の熱雑音(Vn2)は,ボルツマン定数(k)が1.38×10-23[J/K]),絶対温度(T)が27℃で300[K],抵抗値(R)で与えられる周波数特性を持たない雑音と,1次LPFの雑音帯域幅(Δf)の乗算で求められます.
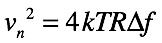 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
回路(a)の抵抗(R1:50Ω)と,コンデンサ(C1:1μF)のカットオフ周波数から式4を使い雑音帯域幅を求めます.
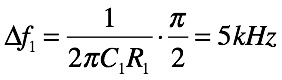 ・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・(6)
式6の雑音帯域幅かつ27℃(絶対温度:T=300K)の条件で発生する抵抗の熱雑音 (Vn1)は,
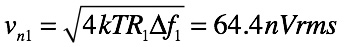 ・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・(7)
式7で求めた64.4nVrmsが回路(a)の全出力雑音電圧です.
同様(式8)に,回路(b)の抵抗(R2:50Ω)と,コンデンサ(C2:0.6366198μF)のカットオフ周波数から式4を使い雑音帯域幅を求めます.
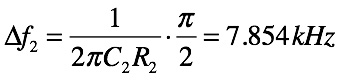 ・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・(8)
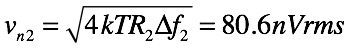 ・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・(9)
式9で求めた80.6nVrmsが回路(b)の全出力雑音電圧です.
●1次LPFの雑音をLTspiceで確かめる
ここからはLTspiceを使い1次LPFの雑音帯域幅がカットオフ周波数へπ/2を乗算したものであるかを確かめます.図1の回路(a)と(b)の1次LPFへ信号源を接続し,シミュレーションで得たOUT1とOUT2の全出力雑音電圧と,帯域幅√Hzあたりの雑音電圧を用いて雑音帯域幅を導き出します.これらの結果と式6と式8の手計算で得た値が合うか比較します.
図4は,回路(a)の雑音をシミュレーションする回路で,図5は,回路(b)の雑音をシミュレーションする回路です.「.noise」は,熱雑音やショット雑音,揺らぎ雑音(1/f)の各雑音を対象とする周波数領域のノイズ解析が実行できます.他の解析と同様にメニューバの「Simulate>Edit Simulation Command」から入力や出力,周波数の範囲を設定します.また「.MEAS」コマンドを用いて1回のシミュレーションで全出力雑音電圧[Vrms]や帯域幅√Hzあたりの雑音電圧[Vrms/√Hz],また二つの結果を用いて雑音帯域幅[Hz]を計算させ,ログ・ファイルへ記録する方法を用います.
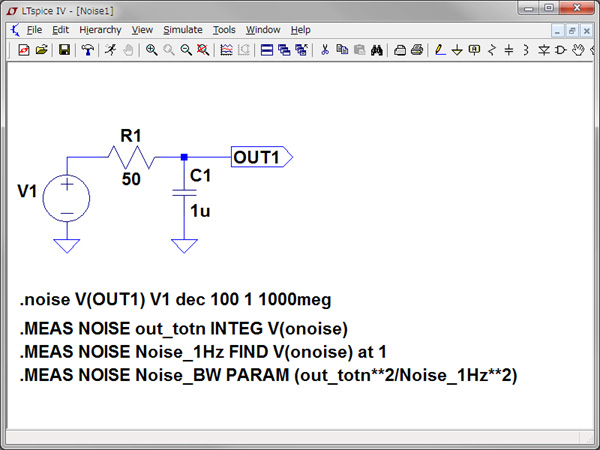
二つの結果を用いて雑音帯域幅[Hz]を計算させ,ログ・ファイルへ記録する方法
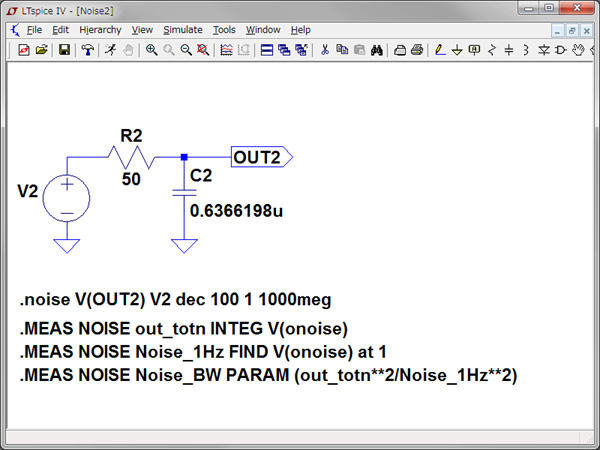
二つの結果を用いて雑音帯域幅[Hz]を計算させ,ログ・ファイルへ記録する方法
●「.MEAS」コマンドを詳しく見てみます
■全出力雑音電圧
全出力雑音電圧はLTspiceの文法から「.MEAS NOISE out_totn INTEG V(onoise)」(図6)となり,内容は,「NOISE解析において,全出力雑音電圧を変数out_totnへ入れなさい」となります.V(onoise)は,「.noise」で指定した出力です.ここでは,V(OUT1)とV(OUT2)の雑音電圧密度で,単位はV/√Hzです.

全出力雑音電圧は式10に相当します.
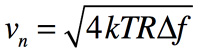 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
■帯域幅√Hzあたりの雑音電圧
帯域幅√Hzあたりの雑音電圧はLTspiceの文法から「.MEAS NOISE Noise_1Hz FIND V(onoise) at 1」(図7)となり,内容は, NOISE解析において,測定周波数1Hzで帯域幅√Hzあたりの雑音電圧を探し変数Noise_1Hzへ入れなさいとなります.
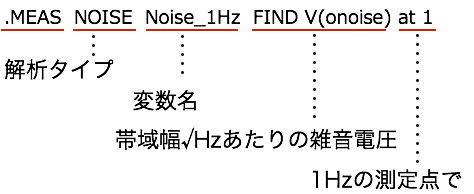
帯域幅√Hzあたりの雑音電圧は式11に相当します.
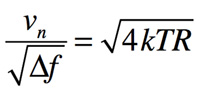 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
■雑音帯域幅
雑音帯域幅は,全出力雑音電圧と√Hzあたりの雑音電圧を用いて求めます.具体的には式12を「.MEAS」のPARAMを用いて同時に計算させます.
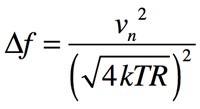 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(12)
「.MEAS NOISE Noise_BW PARAM (out_totn**2/Noise_1Hz**2)」(図8)となり,内容は,「NOISE解析において,全雑音電力/雑音パワースペクトル密度から帯域幅を計算しNoise_BWへ入れなさいとなります.
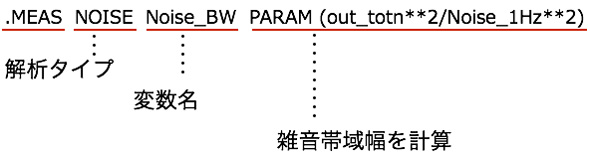
LTspiceでは,「**2」は2乗を表し,「**3」は3乗となる
ログ・ファイルを見るときは,メニューバの「View > SPICE Error Log」または,ショートカット・キーの「Ctrl+L」でログ・ファルのウィンドが現れます.シミュレーション実行後にログ・ファイルには次のように出力されました.
図4[回路(a)]のシミュレーション結果
noise_1hz: v(onoise)=9.10387e-010 at 1
noise_bw: (out_totn**2/noise_1hz**2)=4999.27
周波数1Hz~1GHzで全出力雑音は64. 3694 [nVrms]
帯域幅√Hzの雑音電圧は0.910387 [nV/√Hz]
このときの雑音帯域幅は4.999kHzであり,式6と同等であることが確認できます.
図5[回路(b)]のシミュレーション結果
noise_1hz: v(onoise)=9.10387e-010 at 1
noise_bw: (out_totn**2/noise_1hz**2)=7853.39
周波数1Hz~1GHzで全出力雑音は80. 6779 [nVrms]
帯域幅√Hzの雑音電圧は0.910387 [nV/√Hz]
このときの雑音帯域幅は7.853kHzであり,式8と同等であることが確認できます.
以上のように1次LPFの雑音帯域幅とカットオフ周波数は異なりますので混同しないようにしましょう.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice014.zip
●データ・ファイル内容
Noise1.asc:図4の回路
Noise2.asc:図5の回路
※ファイルは同じフォルダに保存して,フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら










