立ち上がり時間が早い回路はどっち?

図1の回路(a)[R1=200Ω,C1=6800pF]と回路(b)[R2=200Ω,C2=10000pF]は,抵抗とコンデンサで構成した1次ロー・パス・フィルタ(LPF)です.カットオフ周波数は,回路(a)が117.0kHzで,回路(b)が79.6kHzとなります.この回路(a)と(b)に,図2の赤線で示す急峻な立ち上がりの入力波形をV1とV2に印加した場合,青線で示す出力波形の10%~90%区間の立ち上がり時間が早い(3μs)回路はどちらでしょうか?この問題は,ビギナ・エンジニアの方を対象としています.
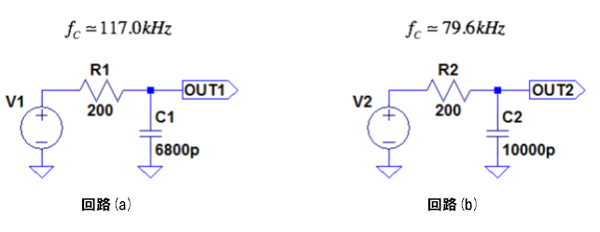
回路(a)[R1=200Ω,C1=6800pF],回路(b)[R2=200Ω,C2=10000pF]
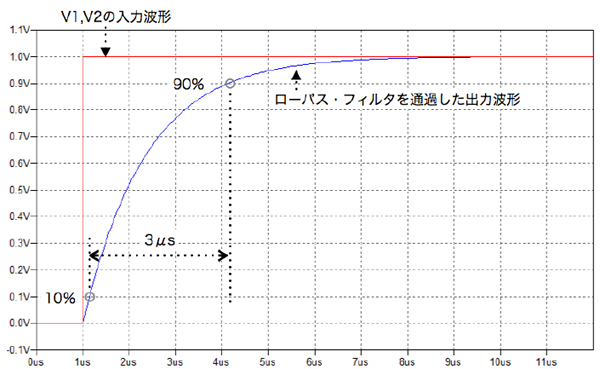
急峻な立ち上がりの入力波形をV1とV2に印加
回路(a)
波形振幅の10%~90%の区間の立ち上がり時間(tr)と1次LPFのカットオフ周波数(fc)は次の関係式になります.
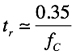 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
式1により,回路(a)の立ち上がり時間はtr=3μsとなり,回路(b)の立ち上がり時間はtr=4.4μsとなります.
●立ち上がり速度とカットオフ周波数の関係式を導きだす
式1は,「扱う信号の高周波成分は1次LPFで減衰させたいけど,出力の立ち上がり時間はある値を守りたい.その時のカットオフ周波数はいくらにしたらいいだろう?」また,その逆の「1次LPFへ矩形波を入力したけど,カットオフ周波数から見込める立ち上がり時間はいくらだろう?」という場合に,回路設計の指標に使えるものです.
図2の赤線のように,ある時間を境に振幅が急に変わる入力を「ステップ入力」といいます.このような,入力をした時の過渡な応答を「ステップ応答」といいます.このステップ応答を入力の矩形波の立ち上がりに見立てて,1次LPFの出力の応答を計算します.ステップ応答の10%~90%区間の立ち上がり速度(tr)と1次LPFのカットオフ周波数(fc)の関係式は,次のように導きだします.
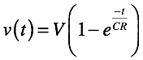 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)式2のv(t)の電圧が10%になる時間をt10,また,90%になる時間をt90とします.v(t)の電圧が10%のとき,式2は,式3となります.
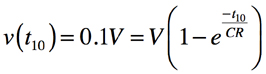 ・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・(3)式3を整理すると式4になります.
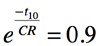 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)式4の両辺のlnを取り整理すると,式5となります.
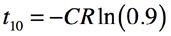 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)次にv(t)の電圧が90%のとき,式2は式6となり,式3,4,5と同様の解き方で式7となります.
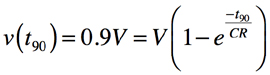 ・・・・・・・・・・・・・・・・・・・・・・(6)
・・・・・・・・・・・・・・・・・・・・・・(6)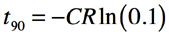 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)立ち上がり時間は「tr=t90-t10」ですので,式5と式7を使って式8となります.
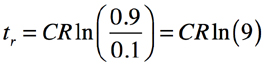 ・・・・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・・・・(8)ここで,1次LPFのカットオフ周波数は式9です.
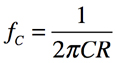 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)式8と式9より,ステップ応答の10%から90%の区間の立ち上がり速度(tr)と1次LPFのカットオフ周波数(fc)の関係は式10となります.
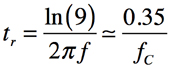 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)回路(a)のfc=117kHzと回路(b)のfc=79.6kHzは,式1より回路(a)の立ち上がり時間は,3μsとなり,回路(b)の立ち上がり時間は,4.4μsと計算できます.
●LTspiceで回路を解析する
図3は,回路(a)と回路(b)のV1とV2へ立ち上がり時間を1nsとした矩形波をステップ入力し,OUT1とOUT2の過渡応答を確認するLTspiceの回路です.ステップ入力は1μsに立ち上がり始め,1.001μs後に振幅が1Vとなります.過渡解析時間は0~12μsとしました.振幅が1Vの10%で0.1Vの時と,90%の0.9Vになる時間をグラフのカーソル機能を用いて,目視で探し出すのは大変です.そこで「.MEAS」コマンドでそれらの時間を探し出します.探し出した値から「.MEAS」コマンドで立ち上がり時間を計算します.また,式1の立ち上がり時間からカットオフ周波数を計算させます.これら一連の解析は1回のシミュレーションで全て終了します.
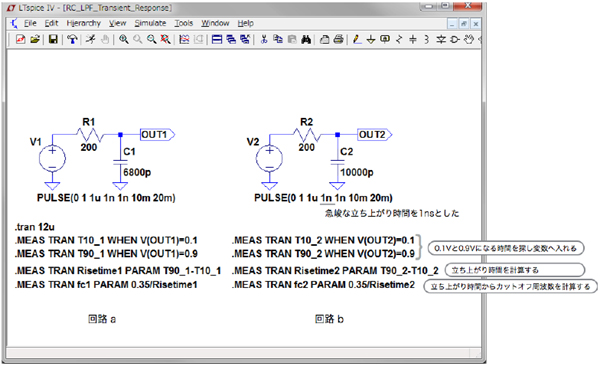
OUT1とOUT2の過渡応答を確認する回路
図4は,図3の解析結果をグラフにしました.赤色は回路(a)と回路(b)の入力したステップ入力の電圧波形です.またグラフの青色は回路(a)のOUT1端子の出力波形,緑色は回路(b)のOUT2端子の出力波形を示します.OUT1端子とOUT2端子の二つの出力波形上にある○印は波形の振幅が0.1V, 0.9Vになる箇所を説明のために付け加えました.シミュレーションしたグラフより,回路(a)の立ち上がり速度が3μsで早いことが分かります.
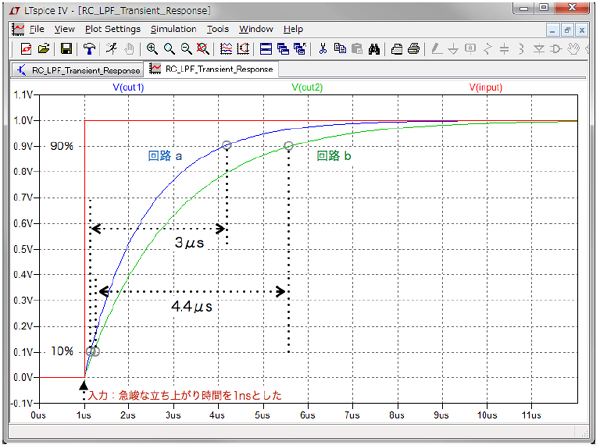
回路(a)の立ち上がり速度が3μsで早いことが分かる
●「.MEAS」コマンドを詳しく見てみます
解析したグラフ上のカーソル機能で波高値が1Vの10%になる0.1Vになる時間と9%の0.9Vになる時間を目視で探し出すのは大変です.また探し出した値から立ち上がり時間(tr)や立ち上がり時間から式1で求めたカットオフ周波数(fc)を一度のシミュレーションで解析できるようにしました.
ここでは,Y軸が指定した値になるときのX軸の値を探し出す「WHEN」や探し出した値を指定の数式を用いて計算する「PARAM」を用います.
OUT2端子が0.1Vになる時間を探すWHENはLTspiceの文法から「.MEAS TRAN T10_2 WHEN V(OUT2)=0.1」(図5)となり,内容は「過渡解析において,OUT2の電圧が0.1Vになる時間を変数Risetime2へ入れなさい」となります.
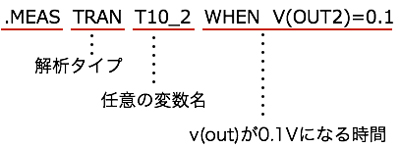
「過渡解析において,OUT2の電圧が0.1Vになる時間を変数Risetime2へ入れなさい」という内容
式1の関係を用いて,別の「.MEAS」コマンドで得られた立ち上がり時間からカットオフ周波数を計算するPARAM指定はLTspiceの文法から「.MEAS TRAN Risetime2 PARAM 0.35/Risetime2」(図6)となり,内容は「過渡解析において,“0.35/Risetime2”を計算し変数fc2へ入れなさい」となります.
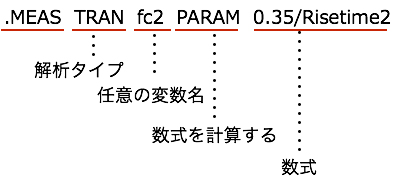
「過渡解析において,“0.35/Risetime2”を計算し変数fc2へ入れなさい」という内容
以上の二つの「.MEAS」を用いて,図3の回路(a)と回路(b)において「OUT1端子が0.1Vになる時間を探す」,「OUT1端子が0.9Vになる時間を探す」,「0.1V~0.9V間の立ち上がり時間を計算する」,「立ち上がり時間から式1を用いてカットオフ周波数を計算する」の結果はログ・ファイルに記録されます.
ログ・ファイルを見るときはメニューバの「View > SPICE Error Log」または,ショートカット・キーの「Ctrl+L」でログ・ファルのウィンドが現れます.シミュレーション実行後のログ・ファイルには次のように出力されました.
t90_1: v(out1)=0.9 AT 4.13434e-006・・・回路(a)OUT1が0.9Vになる時間
risetime1: t90_1-t10_1=2.99046e-006 ・・回路(a)0.1V~0.9V間の立ち上がり時間
fc1: 0.35/risetime1=117039 ・・・・・・・回路(a)立ち上がり時間からカットオフ周波数を計算した結果
t10_2: v(out2)=0.1 AT 1.21119e-006・・・回路(b)OUT2が0.1Vになる時間
t90_2: v(out2)=0.9 AT 5.60524e-006・・・回路(b)OUT2が0.9Vになる時間
risetime2: t90_2-t10_2=4.39405e-006 ・・回路(b)0.1V~0.9V間の立ち上がり時間
fc2: 0.35/risetime2=79653.2 ・・・・・・・回路(b)立ち上がり時間からカットオフ周波数を計算した結果
回路(a)の振幅の10%~90%に相当する0.1V~0.9V間の立ち上がり時間は,約3μsです.式1の関係よりその時に必要なカットオフ周波数は約117kHzであることが分かります.この周波数は,抵抗R1が200Ωで,コンデンサC1が6800pFとした,カットオフ周波数の式「fc1=1/2πC1R1=117kHz」で得られる周波数と同じです.
同様に回路(b)の振幅の10%~90%に相当する0.1Vから0.9V間の立ち上がり時間は,約4.4μsです.式1の関係よりその時に必要なカットオフ周波数は約79.7kHzであることが分かります.このカットオフ周波数はR2が200Ωで, C2が10000pFとした式「fc2=1/2πC2R2」で得られる周波数と同じです.
このように,式1は,1次LPFにおいて「時間軸」の立ち上がり速度や「周波数軸」のカットオフ周波数の関係を簡単な除算で求められます.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice008.zip
●データ・ファイル内容
RC_LPF_Transient_Response.asc:図3の回路
※ファイルは同じフォルダに保存して,フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら










