ひずみが良い（正弦波に近い）のはどっち？
図1は，ゲイン100dBの電圧制御電圧源を使った，ゲイン2倍(6dB)のアンプです．
このアンプに1kHz，1Vppの正弦波が入力されています．
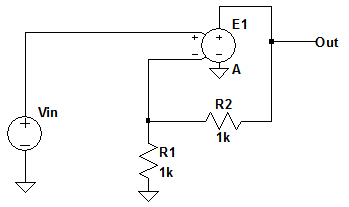
ゲイン2倍(6dB)のアンプに1kHz，1Vppの正弦波が入力されている
負帰還の効果を確認するため，ひずみ成分として3kHz，0.5VPPの正弦波を発生する信号源Vdを，図2の（a）は反転入力端子に挿入し，（b）はE1 と直列に挿入しました．Out端子の出力波形が正弦波に近い（ひずみが良い）のはAとBのどっち？
（a） ひずみ成分を反転入力端子に挿入した回路（入力段にノイズがある場合）
（b） ひずみ成分をE1と直列に挿入した回路（出力段にノイズがある場合）
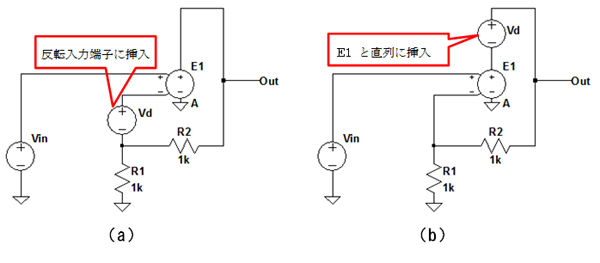
反転入力端子に挿入した回路とE1 と直列に挿入した回路
（b） ひずみ成分をE1 と直列に挿入した回路
電子回路の教科書や解説書で，負帰還にはひずみを低減する効果がある，という説明を読んだことがある方も多いと思います．しかし，低減できるのは，出力段で発生したひずみです．入力段で発生したひずみを低減することはできません．
●式を立て比べてみる
図2（a）でE1のゲインをA として，アンプ出力をVout，帰還率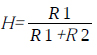
として式を立てると，Vout=(Vin-(Vd+Vout*H))*Aとなり，Vout に関して解くと，
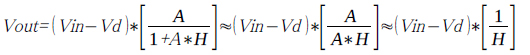・・・・・・（1）
となります．（A*Hは1よりも十分大きいものとします）
（a）の回路のゲインは1/Hですから，ひずみ成分Vd もそのままゲイン倍になることがわかります．
次に図2（b）に関して同様に式を立てると，Vout=(Vin-Vout*H)*A+Vd となり，Vout に関して式を解くと
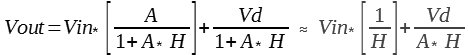・・・・・・・・・・（2）
式（1）と式（2）を比べると，(b)の場合Vinはゲイン倍になり，ひずみ成分Vdは1/(A*H)に減少して出力されることがわかります．式を眺めただけでは実感しにくいので，LTspiceで比較してみます．
●シミュレーション前の，ひずみ解析の注意点
LTspiceでひずみのシミュレーションを行う時に一つ注意する点があります．正弦波がひずむと基本波以外に，2倍，3倍などの周波数の高調波成分が発生します．そこで，LTspice でひずみを定量的に比較する場合，この高調波成分の量で比較します．その時にFFT（Fast Fourier Transform)解析機能を利用します．FFT を使って高精度な解析をする場合，トランジェント解析の時間刻み幅や出力データの桁数，圧縮設定に注意が必要です．
図3は，基本的なアンプです．この回路をFFT解析設定確認用として使って，解析設定の違いで，解析結果がどのように変わるか実験します．
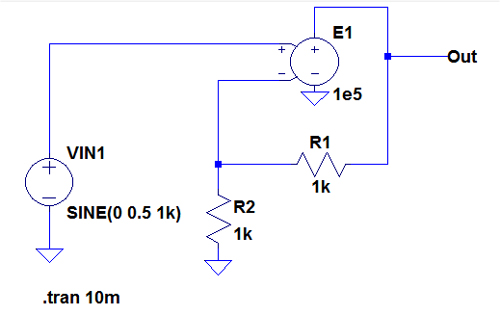
解析をする場合，トランジェント解析の時間刻み幅や出力データの桁数，圧縮設定に注意
まず，トランジェント解析でSTOP TIMEだけ指定して解析します「.tran 10m」．解析終了後，Out端子の波形をプロットしたら，FFT解析結果を表示するため図4のように[View][FFT]を選択します．
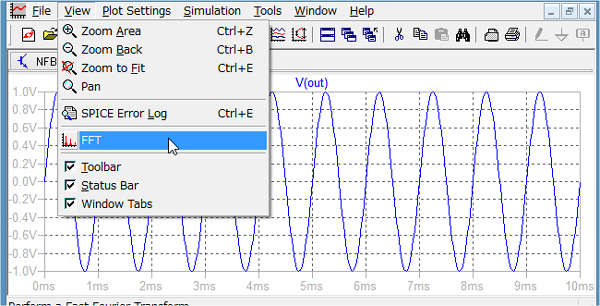
[View][FFT]を選択
「Select Waveforms to include in FF」というウィンドウが表示されます．デフォルトの設定で良いので，そのまま[OK]ボタンを押します．すると図5のようなFFT解析結果が表示されます．
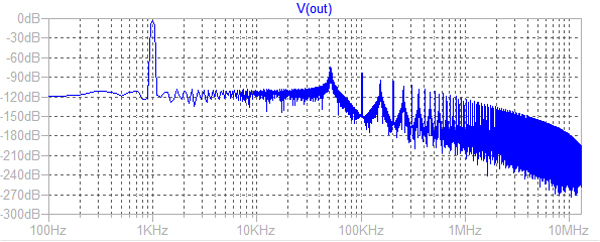
デフォルトの設定で良い
次に解析精度を上げるため，トランジェント解析の最大刻み時間幅を追加します．「.tran 0 10m 0 0.1u」に変更します．トランジェント解析後，[View][FFT]を再度選択する必要があります．再度選択をしないとFFT解析結果の画面の情報が更新されません．図6がその解析結果です．10kHz以上の波形が若干変わっているのがわかると思います．スペクトラムとして，きれいなグラフを出すのであれば，「.tran 0 50m 0.01u」位にすると高域のノイズ・フロアもほとんど平らになります．しかし，シミュレーション時間が若干長くなります．
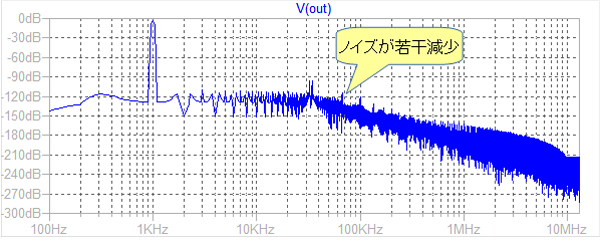
10kHz以上の波形が若干変わっている
そこで，次は[SPICE Directive]でオプション設定を追加します．[SPICE Directive]を選択後，「.option plotwinsize=0 numdgt=15」と入力します．これは解析結果出力の圧縮を禁止し，データの桁数を15桁(デフォルトは6 桁）に変更するオプション設定です．この設定で解析した結果が図7になります．余計なノイズが減少し，解析精度が上がっていることがわかります．ノイズ・フロアは-120dB程度だったものが，-280dB程度に減少しています．
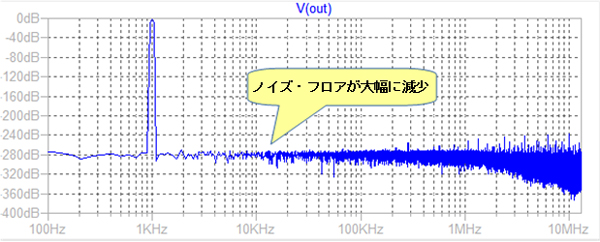
以降の解析はこの図7と同じ設定で実施することにします．また，ひずみ解析には「.four」 コマンドを使用することもできるので，「.four 1k V(Out) 」というコマンドを追加しておきます．
●回路（a）を確認する
図8が（a）のシミュレーション用の回路です．ひずみ成分Vdは出力のひずみ波形をわかり易くするために振幅を-0.25 として，位相を反転して加えています．図9がそのシミュレーション結果になります．
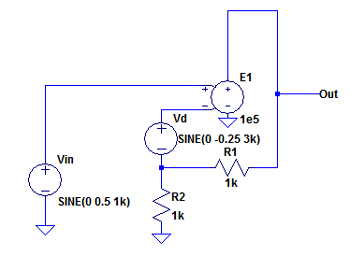
ひずみ成分を反転入力端子に挿入
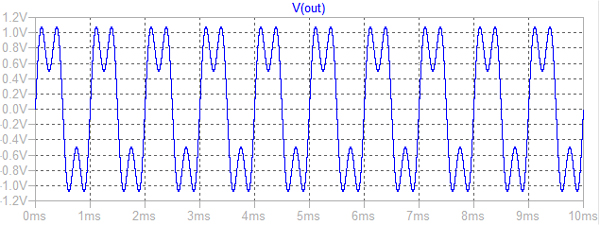
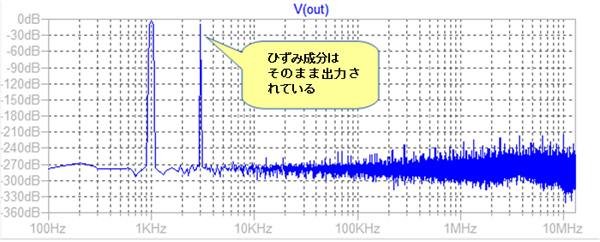
正弦波とはほど遠い波形となっている
正弦波とはほど遠い波形となっていて，図9のFFT解析でも1KHz成分の-6dB程度の3kHz成分が存在していることがわかります．
「.four」 コマンドの結果を確認するには回路図ウィンドウをアクティブにしてキーボードで「Ctrl＋E」と入力します．すると図11のようにテキストで解析結果が表示されます．
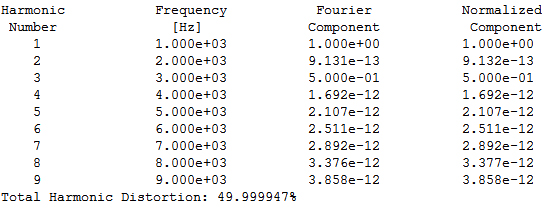
THD(Total Harmonic Distortion）は約50%
1kHz成分が1Vで，3kHz成分が0.5V となっていて，入力の0.5V とひずみ成分として加えた0.25Vがそのまま加算され，2倍になっていることがわかります．基本波と，すべての高調波の二乗和平方根の比であるTHD(Total Harmonic Distortion）は，約50%となっています．
●回路（b）を確認する
次に図1（b）の回路を同様にシミュレーションしてみます．図12が（b）のシミュレーション用の回路です．
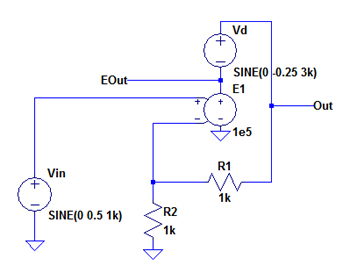
ひずみ成分をE1と直列に挿入
図13がシミュレーション結果です．見た目はきれいな正弦波になっています．
次にFFT解析結果を見てみます．
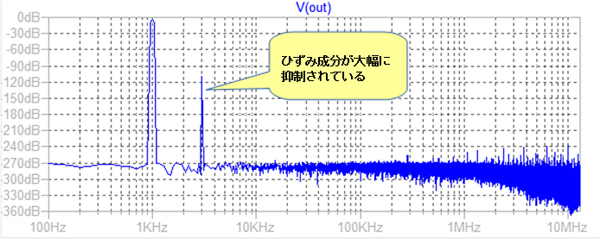
図14が回路（b）のFFT解析結果です．3kHz成分は1kHz成分よりも100dB以上小さいことがわかります．「.four」解析の結果も図13のように3kHz成分は5uV程度に減少していることがわかります．THDは0.0005%です．
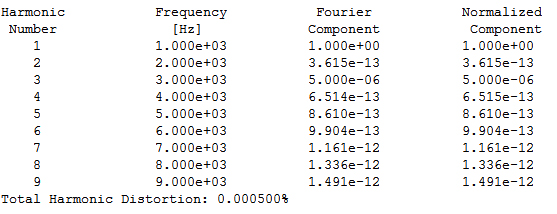
THDは0.0005%
●負帰還という技術の不思議さ，素晴らしさ
つまり，問題の回答である，ひずみが良いのは，「（b）ひずみ成分をE1 と直列に挿入した回路」ということがシミュレーションからも確認できました．
この解析結果を見て，「回路（b）で，加算したひずみ成分は，いったいどこに消えてしまったのだろうか？」という疑問を持つ方がいるかもしれません．
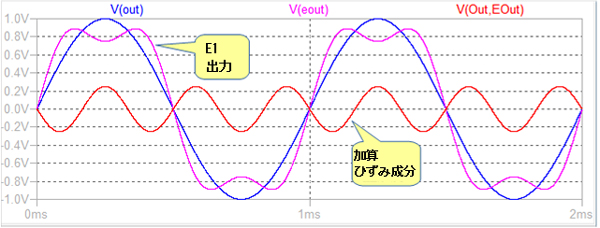
図16は，加算したひずみ成分，電圧制御電圧源E1の出力とV(out)を重ね書きしたものです．負帰還の効果によってV(out)の波形が入力電圧と相似形になるよう，電圧制御電圧源E1の出力が自動的に調整されます．言い換えると，E1の出力がひずむことで，加算されたひずみ成分を打消し，出力のひずみが小さくなっている，ということになります．これを見ると，負帰還という技術の不思議さ，素晴らしさが実感できると思います．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice007.zip
●データ・ファイル内容
NFB.asc：図3の回路
NFB_A.asc：図8の回路
NFB_B.asc：図12の回路
※三つのファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
