回路の基本的な素子コンデンサの電圧と電流
図1は，47μFのコンデンサ(C1)に，周波数が50Hz，実効値が1Vの交流電圧V1を印加した回路です．コンデンサに流れる電流は，V1を基準にすると位相は進みます．
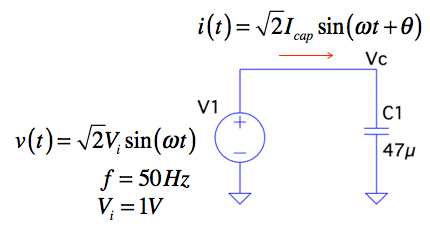
図2は，図1のV1の交流電圧v(t)とコンデンサに流れる電流i(t)を図示しました．(a)と(b)は電流の実効値が14.8mA，(c)と(d)は10.5mAです．また，(a)と(c)は，i(t)がv(t)より位相が90°進み，(b)と(d)は45°進んでいます．図1の回路で，C1に流れる電流i(t)は，図2の(a)～(d)のどれでしょうか？
図1のC1に流れる電流は，図2の(a)～(d)のどれか．
今回は，コンデンサの電圧と電流の関係について解説します．コンデンサに流れる電圧と電流は「i(t)=C1*dv(t)/dt」の関係があります．「v(t)=√2*ViSIN(ωt)」より，i(t)の時間変化を求めると分かります．
コンデンサに流れる電流は，容量，電圧，時間で表すと，式1の関係があります．
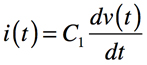・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
また，電圧は式2であり「ω=2πf」です．
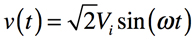・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
図1より，コンデンサ(C1)の容量は47μF，電圧の振幅は「√2*1V」，周波数(f)は50Hzより「ω=100π」です．式2を式1へ代入し整理すると式3となります．
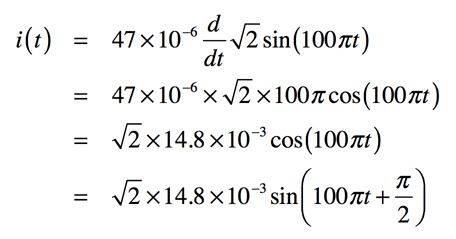・・・・・・・・・・・・(3)
式3より，電流の実効値は14.8mAで，周波数(f)は電圧と同じ50Hzです．また，式2のv(t)と比べると，位相(π/2)が90°進むことが分かります．
以上より，解答は(a)となります．
●コンデンサは誘電体を挟んで2つの電極
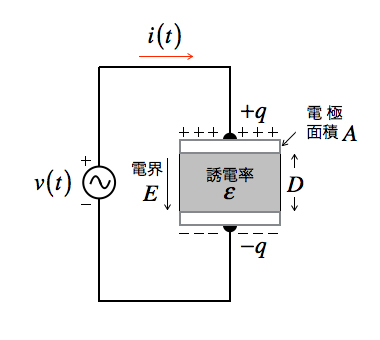
図3は，2つの電極が誘電体によって分離されたコンデンサのモデルを使い，図1を書き直しました．コンデンサは誘電体を挟んで2つの電極があります．2つの電極は，距離がDだけ離れており，誘電体の誘電率をε，また，2つの電極間の電界をEとして表しています．
コンデンサに電圧を印加すると，1つの電極に電子が集まって-qとなり，もう1つの電極には電子が少なくなって+qとなります．コンデンサに交流電圧を印加したとき，+qと-qの状態が入れ替わり，充放電を繰り返すことから交流電流を通す動作となります．コンデンサの単位はファラド(F)を使い，1秒間に電流が1A変化したとき，電圧が1V変化すれば1Fとなります．
●コンデンサの電圧と電流の比例関係を導く
ここでは図3用いて，コンデンサの電圧と電流の関係を導き，コンデンサの性質を理解します．図3の電極の面積をA，誘電体の誘電率をεとすれば，電界(E)は式4となります．
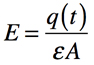・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
コンデンサの電極間の電圧は式4と2つの電極間の距離(D)より，式5となります．
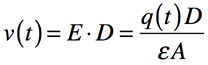・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
電流は電荷の時間変化ですので，式5を使うと，式6となります．
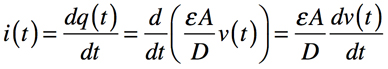・・・・・・・・・・・・・・・・(6)
また，コンデンサの静電容量は電極の面積(A)，誘電率(ε)，電極間の距離(D)より，式7で表せます．
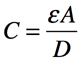・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式7を使って式6を書き直すと，コンデンサに流れる電流は式8となり，解答の計算で使った最初の式1が導出されました．解答では式8を使い，電流の実効値と位相を調べています．
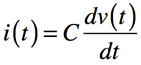・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(8)
また，式8より，コンデンサに電流を印加したときの電圧変化は式9となります．
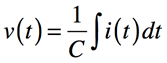・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
コンデンサの電流と電圧の比例関係は，式8と式9です．オームの法則である抵抗(R)，電圧(V)，電流(I)の比例関係「V=RI」と同じように，式9の積分した電流は電圧と比例関係にあることが分かります．例えば，定電流源でコンデンサを充電し，ある電圧までの充電時間をタイマとした回路設計では，式9を用います．
●コンデンサに流れる電流をLTspiceで確かめる
図4は，図1をシミュレーションする回路で，コンデンサに流れる電流を調べます．流れる電流は，赤の矢印方向をプロットします．LTspiceでC1に流れる電流をプロットするとき，マウスをC1の上に置いて左クリックすれば表示できます．しかし，電流はGNDからV1に向かうこととなり，プロットしたい電流の方向は逆となります．演算して電流の向きをV1からGNDへ直せますが，ここでは直感的に理解しやすいように，0Vの電圧源を電流計の代わりに使用します．図4では，V2のプラスからマイナス方向へ流れる電流を表示させます．
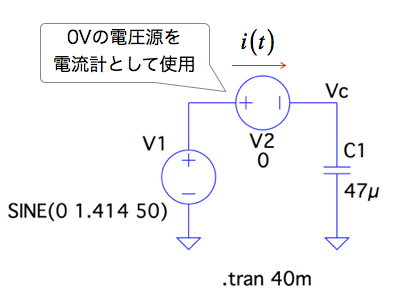
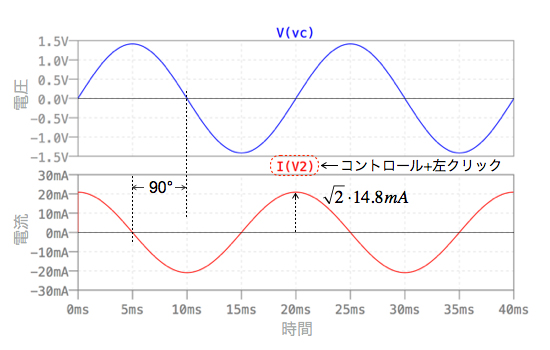
図5は，図4のシミュレーション結果です．まず，電流波形の振幅をカーソルで調べると20.9mAです．これは，√2×14.8mAと同じであり，解答の実効値と同じであることが分かります．
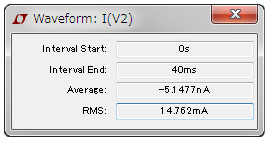
実効値は，LTspiceでも求めることができ，図5のプロットで，電流波形のラベルの上にマウス・カーソルを置き「Ctrl＋左クリック」で図6の小さなウィンドウが開きます．この中のRMSの箇所が実効値であり，14.8mAであることが分かります．
プロットしている波形のラベルの上で，Ctrlキーを押しながら左クリック
次に電圧が0Vと交差する時間と電流が0Aと交差する時間に着目します．解答の計算で得たように，コンデンサに流れる電流は，電圧を基準とすると90°進みます．図5では，電圧が0Vと交差する時間より手前の時間で，電流は0Aと交差しており，1/4周期だけ進んでいることが分かります．1周期は360°（弧度法で2π）ですので，1/4周期は90°（弧度法でπ/2）となり，解答の計算と同じになります．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice3_002.zip
●データ・ファイル内容
CL_Current.asc：図4の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs
