グラフィック・イコライザでブースト状態の回路はどっち？
図1の回路(a)と(b)は，OPアンプとトランジスタを使用した5バンドのグラフィック・イコライザから，1kHzの1バンド部分を切り出したものです．ボリュームの摺動子を動かすことで，1kHzを中心とした音をブースト（ゲイン増大）したり，カット（ゲイン減少）したり，できるようになっています．
回路(a)は，ボリュームの摺動子が上端（R4側）の状態にあります．また，回路(b)は，ボリュームの摺動子が下端（R3側)の状態あります．この二つの状態のとき，1kHzのゲインが増大され，信号がブーストされるのは，回路(a)と(b)のどちらでしょうか．
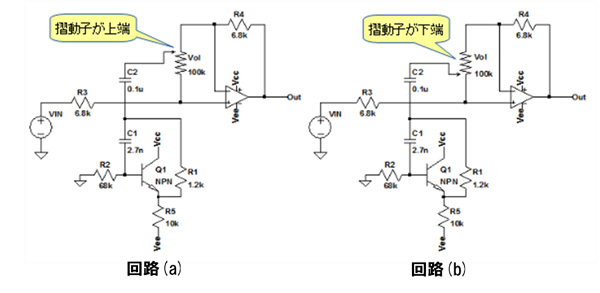
回路(a)はボリュームの摺動子が上端（R2側)の状態にある．
回路(b)はボリュームの摺動子が下端（R1側)の状態にある．
回路(a)
回路(a)と(b)のトランジスタ（Q1）とコンデンサ（C1，C2），抵抗（R1，R2，R5）から構成された回路は，RLC直列共振回路としての働きを行います．通常，RLC直列共振回路は，抵抗とコイル，コンデンサで構成されます．しかし，回路(a)と(b)ではコイルを使用せずに，抵抗とトランジスタ，コンデンサで構成しています．共振回路は，共振周波数を定めて，定めた共振周波数（ここでは1kHz)のときに，最もインピーダンスが低くなる働きを行います．
そこで，回路(b)は，OPアンプのプラス（非反転）端子に共振回路が接続される状態になり，入力信号は共振周波数で減衰します．一方，回路(a)は，OPアンプのマイナス（反転）端子に共振回路が接続される状態になり，共振周波数でアンプのゲインが増大します．つまり，1kHzがブーストされるのは回路(a)の状態です．回路(b)は，1kHzがカットされた状態になります．
●コイルの働きをトランジスタ回路で構成する
今回は，グラフィック・イコライザの回路を例に，RLC直列共振回路をトランジスタ回路で実現する方法を解説します．回路(a)と(b)のトランジスタ（Q1）とコンデンサ（C1），抵抗（R1，R2，R5）から構成された回路は，RLC直列共振回路のコイルと抵抗の働きを行います．このように，トランジスタで構成した回路が，コイルのような働きをする回路を「半導体インダクタ」と呼ばれています．
図2右は，半導体インダクタの動作を解析するための回路です．図1（図2左）のQ1とR5のエミッタ・フォロワは，図2右のE1（ゲイン1の電圧制御電圧源）に置き換えています．E1の出力電圧は，IN-Eと同じ電圧になります．R1にはIN-1からIN-Eを引いた電圧が加わることになります．
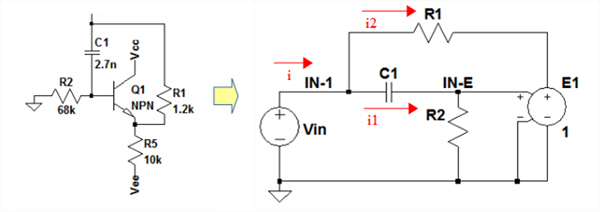
エミッタ・フォロワは電圧制御電圧源(E1)に置き換えている．
●半導体インダクタの働きを計算式で立証
半導体インダクタがRLC直列共振回路のコイルと抵抗の働きをするか調べるために，図2の回路のIN-1端子のインピーダンス（ZIN-1）を計算してみます．Vinからの電流をi，C1に流れる電流をi1，R1に流れる電流をi2とし，C1のインピーダンスをZとして計算します．
IN-1端子のインピーダンス（ZIN-1）は式1となります．
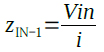・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
Vinからの電流(i)は式2になります．
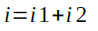・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
C1に流れる電流(i1)は式3になります．
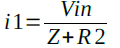・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
R1に流れる電流(i2)は式4になります．
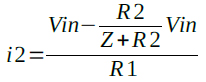・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
式1に，式2，3，4を代入しZIN-1を求めると式5になります．
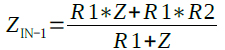・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)
さらに，式(5)に「Z＝1/jωC1」を代入して整理すると式6が求まります．
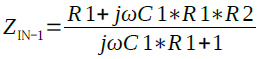・・・・・・・・・・・・・・・・・・・・・・・・・(6)
式7は，抵抗（R）とコイル（L）を直列接続した回路のインピーダンス(ZL)となります．
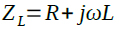・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)
式6の分母の「jωC1*R1」が1より充分に小さい周波数の場合，式6の分母は1とみなせます．その場合，式6の分子「R1+jωC1*R1*R2」と式7の「R+jωL」から「L＝C1*R1*R2」となります．このことから，図2の半導体インダクタが，RLC直列共振回路のコイルや抵抗と等価な働きをすることがわかります．
●半導体インダクタとコイルの働きをLTspiceで検証
図3(a)は，半導体インダクタのインピーダンス特性を，図3(b)のコイルのインピーダンスと比較するためのシミュレーション用の回路です．図3(b)のL1のインダクタの値は，「L＝C1*R1*R2」という値に設定しています．
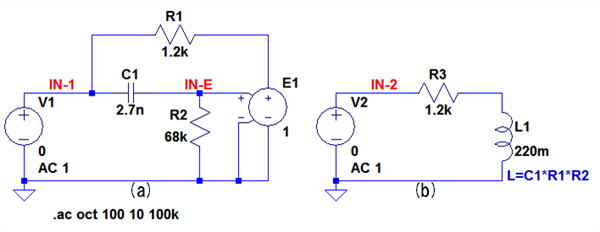
L1のインダクタンスは「L＝C1*R1*R2」という値に設定している．
図4は，図3のシミュレーション結果です．10kHz以下の周波数ではIN-1[図3(a)]とIN-2[図3(b)]のインピーダンスの周波数特性はほとんど同じであることがわかります．また，10kHz以上の高い周波数では差が出てきます．これは，理想インダクタ（コイル）のインピーダンスは周波数とともに増大するのに対し，半導体インダクタのインピーダンスの上限は，R2（68,000Ω）で決まっているためです．
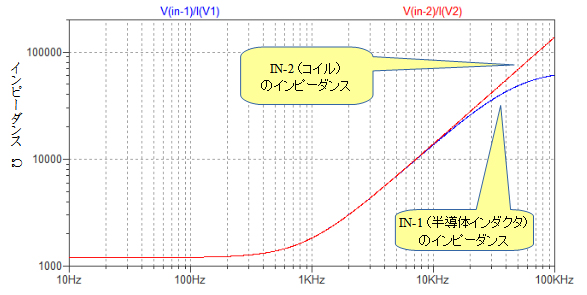
10kHz以下の周波数ではIN-1とIN-2のインピーダンスはほとんど一致している．
●共振周波数と係数Qの求め方
図1の回路(a)と(b)は，半導体インダクタとコンデンサ(C2)で共振回路を構成しています．共振回路を設計する場合，まず，共振周波数f0（ここでは1kHz）と共振の鋭さを表す係数Q(Quality factor)を求めます．
共振周波数f0は式8で計算できます．
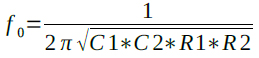・・・・・・・・・・・・・・・・・・・・・・・・・(8)
共振の鋭さを表す係数Qは式9で計算することができます．
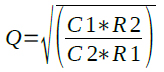・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(9)
そこで，図1の回路(a)と(b)の共振周波数と共振の鋭さを表す係数を式8と式9を使用して調べてみます．図1の回路(a)と(b)の定数を式8に代入すると共振周波数は「f0＝1.07kHz」となります．また，式9から共振の鋭さを表す係数は「Q＝1.23」となっています．
共振の鋭さを表す係数は，数値が大きくなると共振は鋭くなり，数値が小さくなると共振は広くなります．例えばバンド数が多いグラフィック・イコライザは，共振を鋭くします．逆にバンド数が少ないグラフィック・イコライザは，共振を広くします．
●共振特性のシミュレーション
図5は，図1の回路(a)と(b)の共振回路のインピーダンスをシミュレーションするための回路です．図3(a)の回路にC2が追加されています．
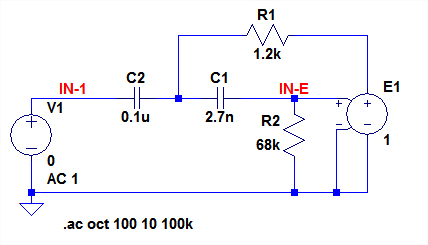
図4の回路にC2を追加．
図6が図5のシミュレーション結果です．共振周波数は約1.07kHzで，その時のインピーダンスは約1.23kΩとなっています．このインピーダンスの値は，R1(1.2kΩ)とほぼ同じ値になります．
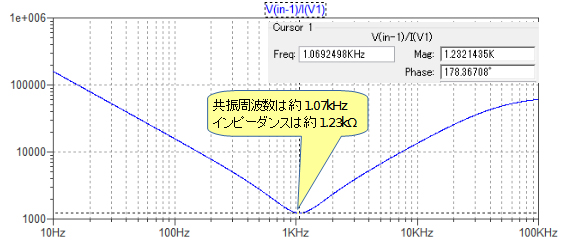
共振周波数は約1.07kHzで，その時のインピーダンスは1.23kΩとなっている．
●回路(a)と(b)のゲインを計算する
図7(a)(b)は，計算式で図1の回路(a)と(b)のゲインを導くために，共振回路をZ0として，回路(a)と(b)の状態を簡略化した回路図です．図7(a)は，回路(a)の1kHzを中心とした音をブーストした状態を表すためにZ0がOPアンプのマイナス（反転）端子に接続しています．図7(b)は，回路(b)の音をカットした状態を表すためにZ0がOPアンプのプラス（非反転）端子に接続しています．ボリュームは固定抵抗(RVol)に置き換えています．しかし，固定抵抗(RVol)は，OPアンプのプラス端子とマイナス端子の両方に接続されているため，ゲインには大きな影響はありません．
図7(a)のZ0は，マイナス端子に接続されているため，ゲインは式10になります．また，図7(b)のZ0は，プラス端子に接続されているため，信号は減衰し，ゲインは式11になります．式10，式11のゲインの計算は，Z0は，図6から読み取ったインピーダンス約1.23kΩの値を使用しています．
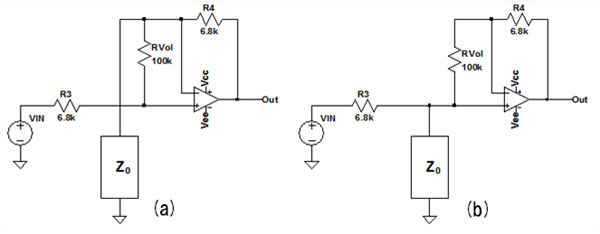
(a)はZ0がマイナス端子に，(b)はプラス端子に接続されている.
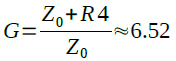・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(10)
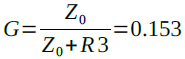・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(11)
このように，計算式からゲインが増大（ブースト）するのは回路(a)ということがわかりました．
●1バンド・グラフィック・イコライザのシミュレーション
図8は，図1の回路(a)と(b)の状態をシミュレーションするための回路です．ボリュームは，「RVoL1A」と「RVoL1B」の2本の抵抗に分割し，抵抗値はVoL1という変数を使って指定しています．RVoL1Aの値は「100k*(1-VoL1)+1m」となっているので，VoL1の変数が1の時は1mΩで，0の時は約100kΩです．RVoL1Bの値は「100K*VoL1+1m」となっているので，VoL1の変数が1の時は約100kΩで，0の時は1mΩになります．このようにして，VoL1という変数でボリュームの位置を指定します．また，図8では「.step」コマンドでVoL1の変数を「0，0.5，1」と変化させてシミュレーションを実施します．
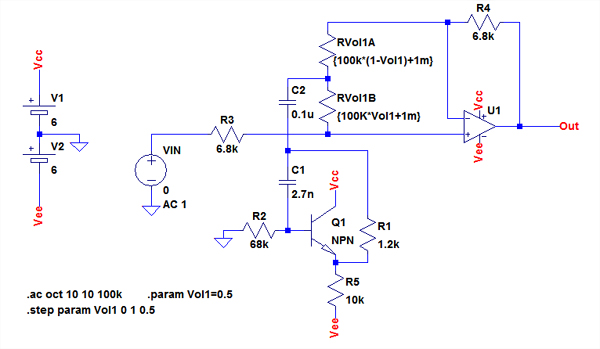
VoL1という変数を使ってボリュームを表現している．
図9が図8のシミュレーション結果です．ボリュームを変えることで，ゲイン特性がブーストとカットに変化することがわかります．
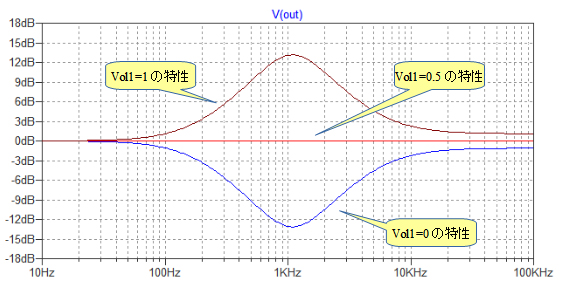
変数VoL1の変数の値でブースト特性やカット特性に変化している．
●5バンド・グラフィック・イコライザのシミュレーション
最後に5バンドの周波数帯のコントロールができる，グラフィック・イコライザの回路とシミュレーション結果を紹介します．図10がシミュレーション用の回路です．
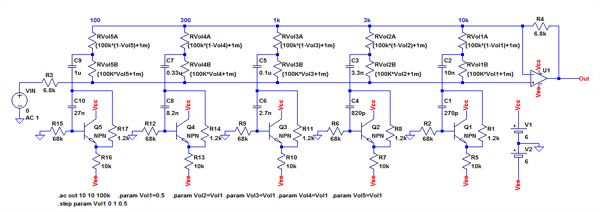
VoL1～Vol5という変数を変えて特性をシミュレーションできる．
図11が図10のシミュレーション結果です．「VoL1～Vol5」という変数を定義して各バンド独立に特性をコントロールできるようにしていますが，図11ではすべて同時に変化させた時のシミュレーション結果となっています．
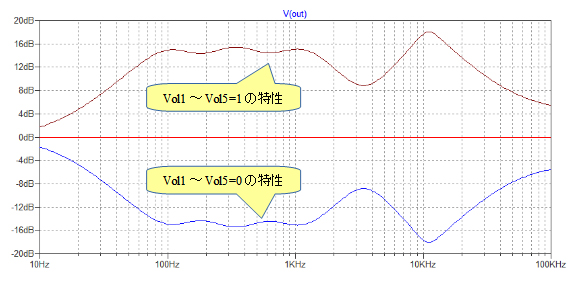
VoL1～Vol5を同時に「0，0.5，1」と変数を変化させている．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice042.zip
●データ・ファイル内容
Solid-state_inductor.asc：図3の回路
Solid-state_inductor_C.asc：図5回路
graphic_equalizer.asc：図8回路
5channel_graphic_equalizer.asc：図10の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
