ΔΣ変調を使用したA-D/D-A変換回路はどっち？

■問題

小川　敦　Atsushi Ogawa

　図1のブロック図(a)と(b)は，どちらもアナログ信号を1ビットのディジタル・データに変換し，伝送路を経由して，ふたたびアナログ信号に変換するA-D/D-A変換システムです．ブロック図(a)と(b)で，ΔΣ変調という技術が使用されているのはどちらでしょうか？

図1　A-D/D-A変換システムブのロック図(a)と(b)
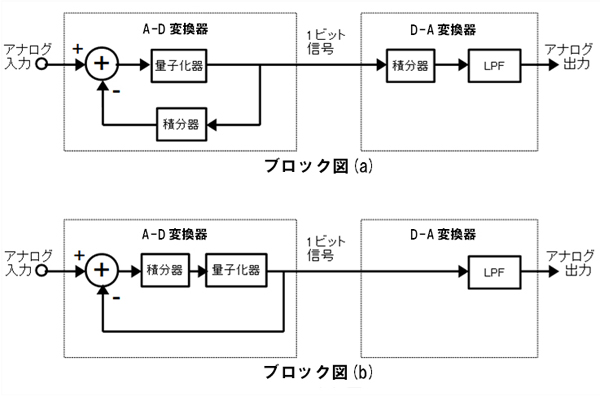
どちらも入力アナログ信号を1ビット・ディジタル信号に変換し，再度アナログ信号に変換している．

■解答

ブロック図(b)
　ブロック図(a)はΔ（デルタ）変調と呼ばれる技術を使ったシステムです．Δ変調では，A-D/D-A変換の両方に積分器が必要です．ブロック図(b)がΔ変調を改良して考案されたΔΣ（デルタ・シグマ）変調という技術を使ったシステムになります．ΔΣ変調は，A-D/D-A変換の積分器を共有にして，A-D変換器に移動できないかと考案されました．

■解説

●日本人が発明したΔΣ変調技術
　オーディオ用をはじめとして，ΔΣ変調技術を利用したA-DコンバータやD-Aコンバータが数多く作られています．この技術の核となる，ΔΣ変調という技術の発明者は日本人の安田靖彦博士です．米国がこの技術の実用化で先行したため，海外発祥の技術のような印象がありますが，1960年ごろに，当時大学院生であった安田氏が考案したものです．

●Δ変調の動作

図1(a)　Δ変調のブロック図
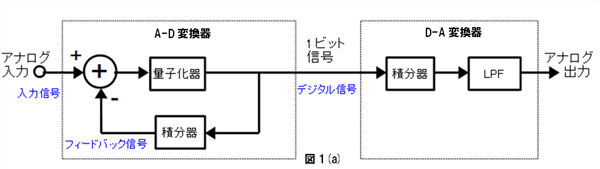
ディジタル信号は，D-A変換器へ伝送される信号とA-D変換器内の積分器でフィードバックする信号になる．

　ΔΣ変調は，ブロック図(a)のΔ変調を改良する過程で考案されました．そこでまず，Δ変調の動作[図1(a)]を解説します．
　入力信号は，まず加算器に入力されます．加算器出力は入力信号とフィードバック信号との差分信号です．ただし，立ち上がりは，フィードバック信号が無い状態で開始します．
　この差分信号は，量子化器で1と－1の2値のディジタル信号に変換されます．（1と0で解説する場合もありますがここでは便宜上1と－1にします．）そして，このディジタル信号は，D-A変換器へ伝送される信号とA-D変換器内の積分器でフィードバックする信号となります．
　加算器で入力信号の方が，フィードバック信号よりも大きい時は，ディジタル・データの1が連続し，フィードバック信号が増大します．逆にフィードバック信号のほうが大きくなると－1が連続してフィードバック信号が減少します．このように，フィードバック信号は，入力信号に追従するような動作となります．
　量子化器からの出力は，1ビットのディジタル・データになるため，ディジタル信号として伝送路で送ることができます．A-D変換器の積分器からのフィードバック信号は，加算器で入力信号と同等のものになっているので，1ビットのディジタル・データをD-A変換器でアナログ信号に戻すためには，D-A変換器の積分器でディジタル・データを積分し，ローパス・フィルタ（LPF）を通してアナログ信号にします．

●ΔΣ変調の動作

図1(b)　ΔΣ変調のブロック図
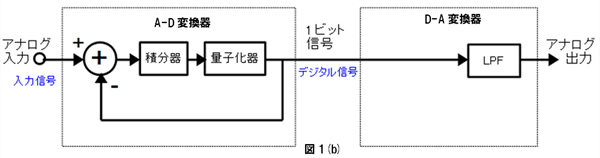
ΔΣ変調は，Δ変調での積分器を共有にして，A-D変換器に移動できないかと考案された．

　Δ変調ではA-D/D-A変換の両方に積分器が必要でした．ΔΣ変調[図1(b)]は，この両方の積分器を共有にして，A-D変換器に移動できないかと考案されたものです．当初は，単純に加算器の前に積分器を置く方式を考えたところ，直流信号入力で破綻するという欠点があったことから，フィードバック・ループの積分器と共有して，加算器の後ろに移動させました．
　入力信号は，まず加算器に入力されます．加算器出力は入力信号と量子化器出力との差分信号です．この差分信号は積分器で積分され，量子化器で1と－1の2値のディジタル信号に変換されます．
　積分器出力が正の場合は，量子化器出力の1が連続し，加算器のマイナス入力端子に加わる電圧は，正の電圧が連続します．負の場合は，量子化器出力の－1が連続し，加算器のマイナス入力端子に加わる電圧は，負の電圧が連続します．
　全体のフィードバック・ループとしては，積分器出力が0に近づくように動作します．この動作によって，入力信号をうまく打ち消すようなディジタル・データ列が生成されることになります．
　量子化器出力は，Δ変調と同様に，1ビットのディジタル・データになるため，ディジタル信号として伝送路で送ることができます．この1ビットのディジタル・データは入力信号に追従し，それを打ち消すような信号となっているため，単純にLPFを通すだけでアナログ信号とすることができます．

●Δ変調システムをLTspiceでシミュレーションする
　図2は，ブロック図(a)のΔ変調システムをLTspiceでシミュレーションする回路です．X1～X3は出力レベルが0～1Vに制限されたOPアンプです（LTspice 電子回路マラソン028 回を参照）．加算器は，抵抗R₁とR₂による単純な加算回路で構成しています．ここで，積分器はX1による反転アンプを使用した積分回路となっています．積分出力の位相が反転するため，R₁とR₂による加算回路で，入力信号と積分出力の差分出力を得ることができます．量子化器はX2によるコンパレータとDフリップフロップ(A1)で構成しています．Dフリップフロップは，LTspiceの「lib\Digtal」フォルダにあるdflopを使用しています．LTspiceのディジタル素子は論理振幅が1V となっているため，アナログ素子もその電圧レベルに合わせています．
　A1のクロック信号は，電圧源VCLKから供給しており，クロック周波数は5MHzとしています．A1のQ出力がディジタル・データとなります．その出力はR₃を介して積分回路に入力しています．Q出力は0Vまたは1Vとなるため，アナログ信号は0.5Vを中心として動作するように，バイアス電圧VBを0.5Vに設定しています．入力信号は0.8VPPで1kHzの正弦波です．
　D-A変換器はX3による積分回路とLPF（X4)で構成しています．LPFの詳細は後述しますが，電圧制御電圧源のLaplace記述を利用した5次バタワース特性でカットオフ周波数100kHzのLPFです．

図2　Δ変調システムをシミュレーションする回路

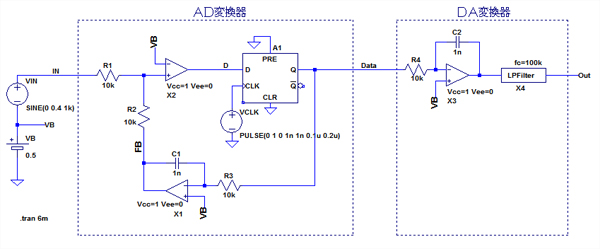
　図3は，入力信号と変換されたディジタル・データ(A1のQ出力)のシミュレーション結果です．下段が入力信号で，0.5Vを中心電圧とした0.8Vppで1KHzの正弦波です．また上段がA-D変換器で変換された1ビットのディジタル・データです．図3の時間軸では，赤一色に塗りつぶされてしまいます．そこで，図4で，時間軸を拡大してみます．

図3　Δ変調のシミュレーション結果
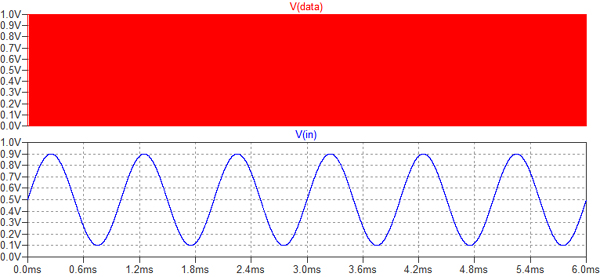
入力信号と1ビットディジタル・データを表示．

　図4は，図3のシミュレーション結果を時間軸を拡大したものです．上段の1ビットのディジタル・データの1と0の変化の様子が確認できます．

図4　時間軸を拡大したΔ変調のシミュレーション結果

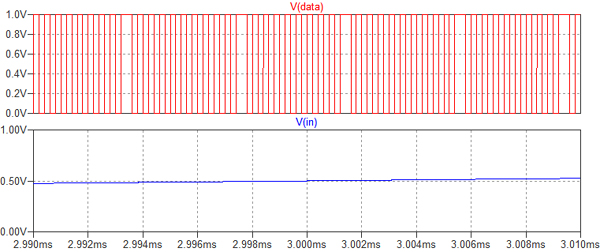
　図5は，D-A変換器で再びアナログ信号となった出力波形です．きちんと入力信号と同じ波形が再現できています．

図5　Δ変調システムでD-A変換したアナログ出力

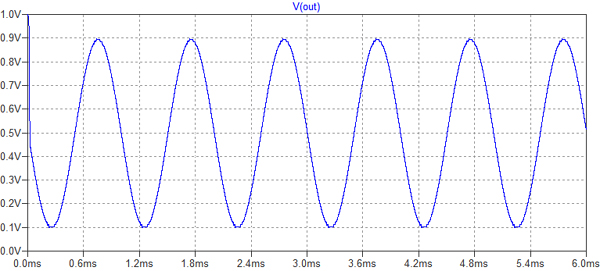
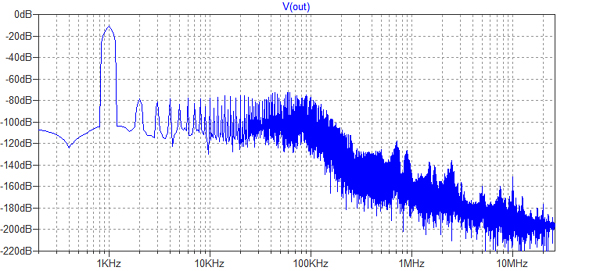
　図6は，この信号をFFT（Fast Fourier Transform：高速フーリエ変換）解析したものです．信号の最初は波形が乱れているため，1m秒～6m秒の信号をFFT解析しています．信号レベルが-10dB程度であるのに対し，高調波成分は-80dB程度となっており，波形ひずみもそれぼど大きくないことがわかります．

図6　Δ変調システムでD-A変換したアナログ出力をFFT解析した結果

●ΔΣ変調システムをLTspiceでシミュレーションする
　図7がブロック図(b)のΔΣ変調システムをLTspiceでシミュレーションする回路です．積分器や量子化器，LPFは図2と同じ構成です．反転アンプを使用した積分回路を，加算器としても使用しています．積分器で位相が反転するため，R₁とR₂で加算することで，入力信号と量子化器出力(A1のQ出力)の差分信号が得られるようにしています．図2と同様，アナログ信号は0.5Vを中心として動作するように，バイアス電圧VBを0.5Vに設定しています．入力信号は0.8VPPで1kHzの正弦波です．

　図7　ΔΣ変調システムをシミュレーションする回路

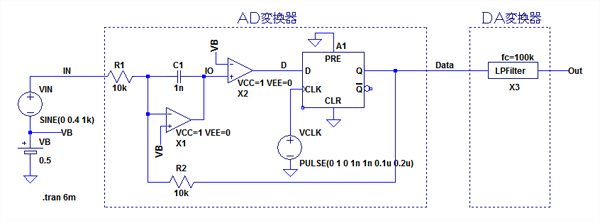
　図8は，ΔΣ変調システムのシミュレーション結果です．下段が入力信号で，0.5Vを中心電圧とした0.8Vppで1kHzの正弦波です．上段が変換後のディジタル・データを表示しています．Δ変調の時と同様に，この時間軸では赤一色に塗りつぶされてしまいます．

図8　ΔΣ変調のシミュレーション結果
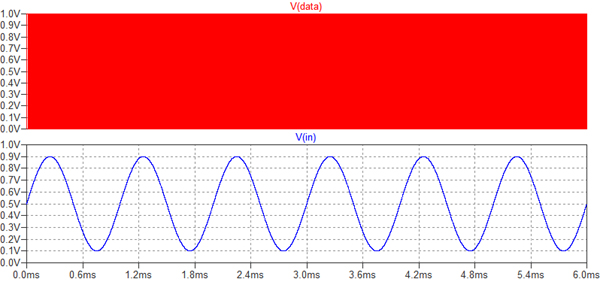
入力信号と1ビットディジタル・データ出力．

　図9は，図8のシュミレーション結果の時間軸を拡大したものです．上段の1ビットのディジタル・データの1と0の変化の様子が確認できます．また，Δ変調システムの図4の上段のディジタル・データとは，1と0の変化の様子が若干異なることがわかります．

図9　時間軸を拡大したΔΣ変調のシミュレーション結果

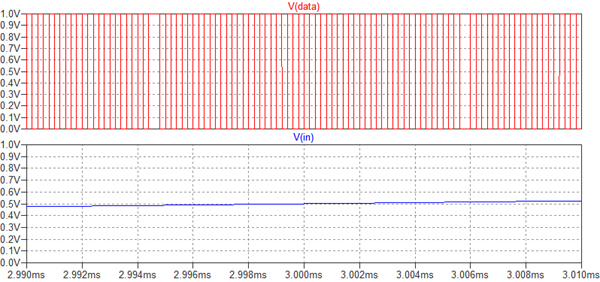
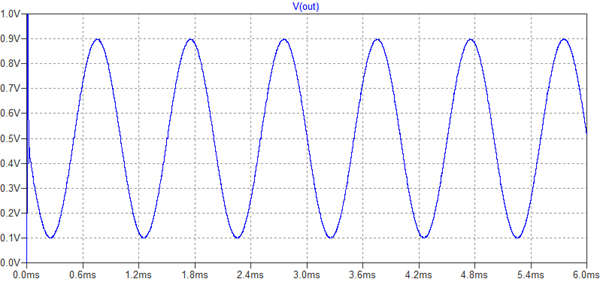
　図10は，1ビット・ディジタル・データのD-A変換（LPF）後のアナログ出力です．入力信号と同等の波形となっています．図10の波形だけを見ると図5のΔ変調のD-A変換（LPF）後のアナログ出力とほとんど差が無いように見えます．しかし，FFT解析をすると差があることがわかります．

図10　ΔΣ変調システムでD-A変換したアナログ出力

●ΔΣ変調特有のノイズ除去機能「ノイズ・シェーピング」
　図11はこの信号のFFT解析結果です．100kHz以上でノイズが減少しているのはLPFの効果ですが，100kHz以下でもノイズの減少が見られます．これはノイズ・シェーピングと呼ばれるΔΣ変調特有のノイズ除去機能によるものです．ノイズを高域に追いやることで低域のノイズを改善しています．
　信号レベルが－10dB程度なのに対し，2次高調波は-100dB程度と図6のΔ変調の時よりもひずみも改善していることがわかります．

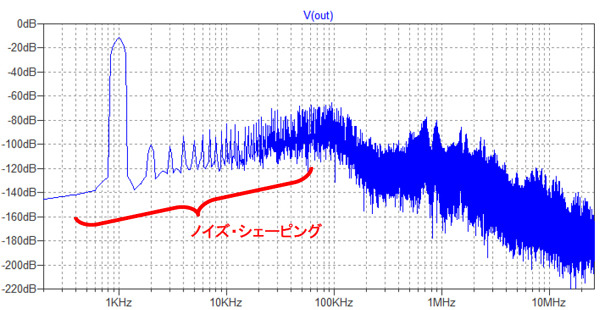
図11　ΔΣ変調システムでD-A変換したアナログ出力をFFT解析した結果
ノイズ・シェーピングの効果が確認できる．

　図7では1ビットデータを直接アナログ信号に変換していますが，一般的にはディジタル信号処理により，1ビット・データ列をサンプリング周波数44.1kHz，16bit といった形式に変換して利用します．ΔΣ変調システムは次数（積分器の個数）を増やすことや，量子化器を多ビット化することなどにより，性能を改善することが可能なため，用途に合わせて色々な工夫を行い，様々な機器に使用されています．

●簡単に任意のカットオフ周波数のフィルタを追加する
　最後に図2や図7の回路で使用したフィルタについて解説します．このフィルタはLTspiceの電圧制御電圧源でLaplace記述が可能なことを利用したものです．Laplace形式でフィルタの伝達関数を記述することにより，任意のフィルタ特性が得られます．図2や図7で使用したのは5次のバタワース特性を持つLPFです．「ω=1」で正規化された5次バタワース特性の伝達関数は式1で示されます．

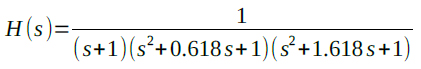・・・・・・・・・・・・・・(1)

　フィルタのカットオフ周波数をfCとし，ωC=2πfCとすると式1は式2のように変形できます．

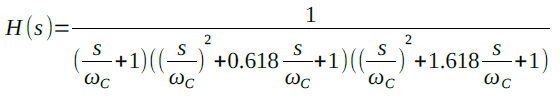・・・・・(2)

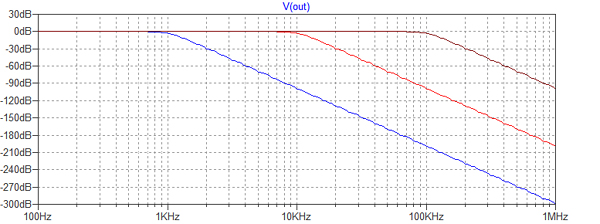
　図12は，このフィルタ回路のサブサーキットです．カットオフ周波数fcをパラメータとして受け取ります．
「.parm wc=fc*2*pi」として，変数wcを定義しています．そして，電圧制御電圧源のパラメータは「Laplace=1/((s/wc+1)*((s/wc)**2+0.618*s/wc+1)*((s/wc)**2+1.618*s/wc+1))」として，式2の伝達関数をそのまま記述しています．

図12　5次バタワース特性LPF　サブサーキット

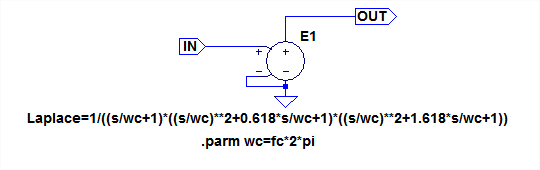
　図13は，このフィルタ・サブサーキットの特性をシミュレーションするための回路です．「.step」でfcを1kHz，10kHz，100kHz と変化させて特性をシミュレーションしています．

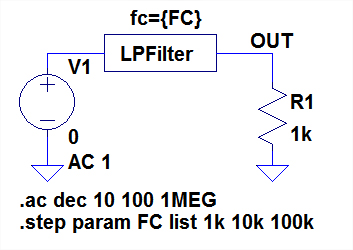
図13　フィルタ・サブサーキットの特性をシミュレーションする回路

　図14は，図13のシミュレーション結果です．所望のカットオフ周波数のフィルタとなっていることがわかります．この手法を用いることにより，いろいろなシミュレーション回路に，簡単に任意のカットオフ周波数のフィルタを追加することが可能なので活用してみてください．

図14　フィルタ特性のシミュレーション結果

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice030.zip

●データ・ファイル内容
delta_J.asc：図2の回路
deltasigma_J.asc：図7の回路
FilterTest.asc：図13の回路
LimitAMP.asc：振幅制限opアンプのサブサーキット
LimitAmp.asy：振幅制限opアンプのシンボルファイル
LPFilter.asc：図12の回路
LPFilter.asy：図12の回路用のシンボルファイル
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください