2段直結増幅回路の出力波形はどれ?

図1は,二つのトランジスタを直結した2段直結増幅回路です.入力信号VINは,1kHzで0.1VPPの正弦波となっています.また,この増幅回路には,図に示したようにOut1とOut2の二つの出力端子があります.
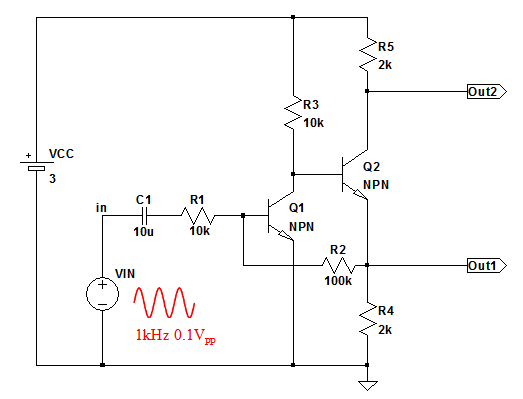
図2は,図1の2段直結増幅回路の出力波形を表示したものです.(A)~(D)はそれぞれ,下段が入力信号波形,中段がOut1の波形,上段がOut2の波形を表示しています.この増幅回路の出力波形として正しいのは(A)~(D)のうちどれでしょう?
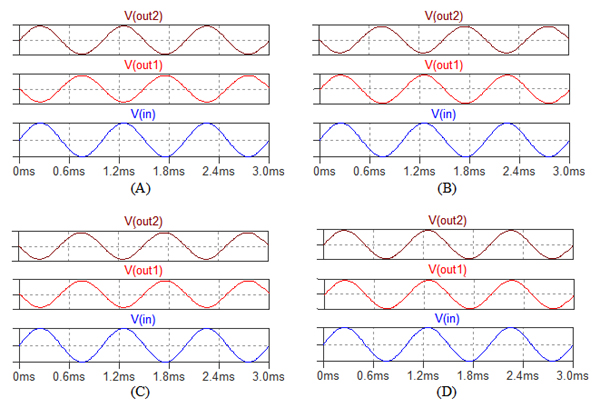
下段が入力信号波形で中段がOut1,上段がOut2の波形.
図2の(A)~(D)の違いは,入力信号波形と二つの出力信号波形の位相です.入力信号に対してOut1の出力の位相がどうなるか,また,Out1とOut2の位相の関係はどうなっているかを考えれば答えがわかります.
接続方法には,それぞれの増幅素子をコンデンサで結合する「コンデンサ結合増幅回路」もあります.コンデンサ結合増幅回路のメリットは,コンデンサで結合するので,バイアス電圧設定の自由度が高くなります.
図1の回路は,Out1からQ1のベースに帰還のかかった反転増幅回路となっています.そのため,Out1の出力波形は入力信号とは逆位相になります.Out1の波形が入力信号と逆位相になっているのは(A)と(C)です.また,Out1の電圧が高くなるとQ2のコレクタ電流が増加し,Out2の電圧は低下します.つまり,Out2の出力波形の位相はOut1とは逆位相になります.(A)と(C)でOut2の出力波形がOut1と逆位相になっているのは(A)です.したがって正解は(A)ということになります.
このように,図1の回路は,一つの増幅回路で位相の異なる二つの出力を得ることができます.例えば,ステレオ・アンプなどで,音の広がりを強調するために逆位相成分を加算するときなどに利用できます.
●2段直結増幅回路の元になる回路
図1は,Out1からQ1に帰還がかかっていますが,その元になっているのが図3の回路です.図3の回路は,Q1によるエミッタ接地増幅回路の出力にQ2のエミッタ・フォロアを接続したものです.エミッタ接地増幅回路の出力は,入力とは逆位相になります.したがって,エミッタ・フォロアの出力も入力とは逆位相になります.
図3では,電圧源VBによってQ1のベースにバイアス電圧を与えていますが,図1の回路は出力端子からQ1のベースに抵抗を介して帰還することで,外部からバイアス電源を印加しなくてもよいようにしたものと考えることもできます.この回路のゲイン(A)はQ1のコレクタ電流をICQ1とすると式1で表されます.
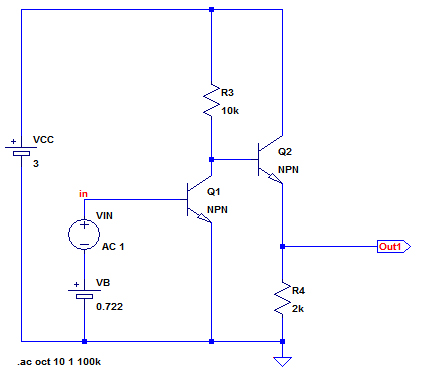
エミッタ接地増幅回路の出力にエミッタ・フォロアが接続されている.
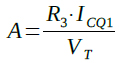 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)
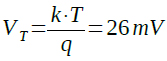 ただし,k:ボルツマン定数,T:絶対温度,q:電子電荷
ただし,k:ボルツマン定数,T:絶対温度,q:電子電荷
●2段直結増幅回路の動作をLTspiceで確認する
図4は,図1のシミュレーション用回路です.図3の回路を元に,Q2のエミッタとQ1のベースをR2で接続し,R1を介して入力信号が加わるようになっています.さらにR5を追加したものと考えることができます.
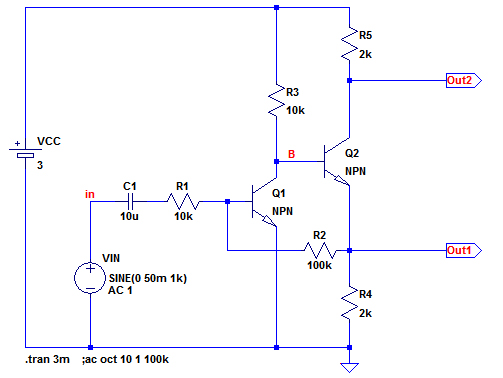
Q2のエミッタからQ1のベースに帰還がかかっている.
まず,シミュレーションでOut1とOut2のゲインを確認する前に,計算でOut1とOut2のゲインの概算を求めシミュレーションの値と比較します.
この回路で,Out1の直流電圧は,ほぼQ1のベース・エミッタ間電圧と等しくなります.厳密には(Q1のベース電流*R2)という電圧が加算されます.B点(Q2のベース)の電圧はOut1の電圧にQ2のベース・エミッタ電圧を加えたものです.また,R3に加わっている電圧はVCCから B点の電圧を引いたものなので,Q1のコレクタ電流(ICQ1)は式2のように概算することができます.
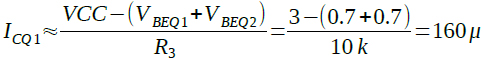 ・・・・・・・・・(2)
・・・・・・・・・(2)
図4の回路は,図3のゲイン(A)の増幅回路に帰還をかけたものなので,Out1のゲイン(G)は式3で計算できます.
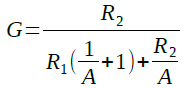 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
式3の帰還がかかっていないゲイン(A)が,十分大きければ「G=R2/R1」という簡単な式になります.式1と式2および図4の定数を使用すると帰還がかかっていないゲイン(A)は式4のように61倍となります.
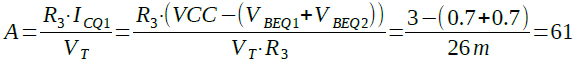 ・・・(4)
・・・(4)
さらに,式4のゲイン(A)の結果(61倍)を式3に代入するとOut1のゲイン(G)は式5のように約8.5倍と計算できます.
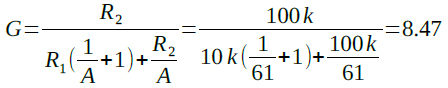 ・・・・・・・・・・・(5)
・・・・・・・・・・・(5)
次に,Out2のゲインを求めるには,Out2の出力直流電圧(VOut2)から求めます.Q2のエミッタ電流(IEQ2)はR2に流れるQ1のベース電流を無視すると,R4に流れる電流と等しくなり「IEQ2=VOut1/R4=350μA」となります.また,Q2のベース電流を無視するとIEQ2はQ2のコレクタ電流ICQ2と等しくなります.R4とR5の抵抗値が等しいので,VOut2は式6のようになります.
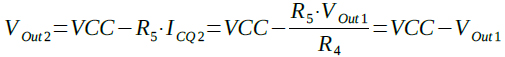 ・・・・・・・(6)
・・・・・・・(6)
この式の信号成分(出力交流電圧)に着目すると「VOut2=-VOut1」となり,Out2のゲインはOut1のゲインと同じことが分かります.これは,Out1とOut2の信号出力振幅は等しく,位相が反転したものになることを表しています.
図5は,図4のシミュレーション結果です.0.1VPPの入力に対し,Out1の出力は位相が反転した0.75VPPとなっています.ゲインは「0.75/0.1=7.5倍」で,式5の計算結果(8.5倍)より若干小さい値となっています.しかし,計算結果は概算なので,ほぼ近似値と言えます.また,Out2の出力は,式6で計算したように,Out1とは逆位相で振幅は同じ0.75VPPとなっています.図5は,正解の図2(A)と同じものです.
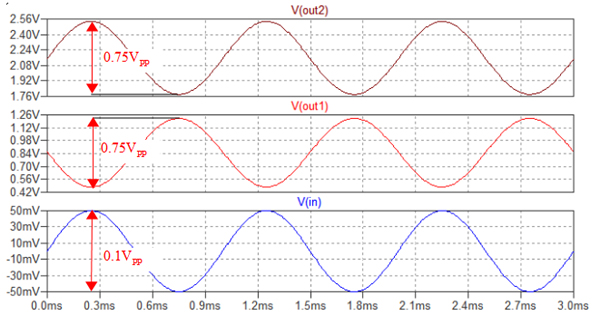
入力とOut1出力は逆位相でOut2出力は入力と同位相となっている.
●2段直結ハイ・ゲイン増幅回路への変更とその動作
図4の回路にコンデンサを一つ追加するだけで,ゲインの非常に大きい増幅回路とすることができます.図6がC2を追加した,ハイ・ゲイン増幅回路です.出力は,Out2から取り出します.R1は削除しても問題ありませんが,図6では配線でショートしてあります.C2を追加することで,図6の回路のQ2はエミッタ・フォロアではなく,エミッタ接地増幅回路として動作します.つまり,エミッタ接地増幅回路が2段縦続接続されることになり,大きなゲインが得られます.また,C2があることで,R2を介してQ1に帰還されるのは直流電圧だけになり,帰還によるゲイン低下もありません.
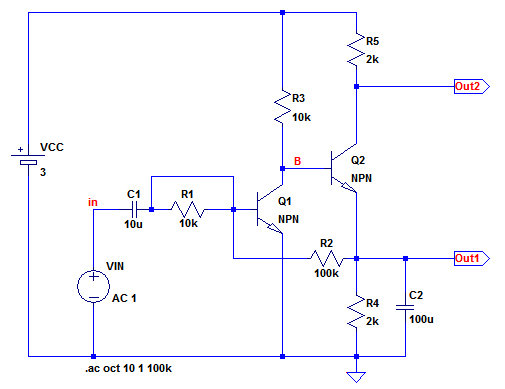
C2を追加することでQ2もエミッタ接地増幅回路として動作する.
この回路のゲイン(G)は,Q2の入力抵抗をRinQ2とすると式7で表されます.
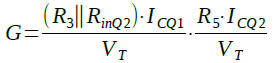 ・・・・・・・・・・・・・・・・・・・・・・・(7)
・・・・・・・・・・・・・・・・・・・・・・・(7)
ここでRinQ2は式8で計算することができ,7.4kΩとなります.
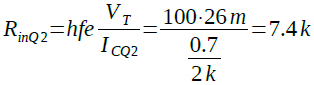 ・・・・・・・・・・・・・・・・・・・・(8)
・・・・・・・・・・・・・・・・・・・・(8)
式8の値を式7に代入すると式9のように712倍(57dB)という大きなゲインになることがわかります.
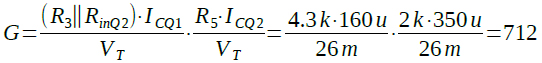 ・・・・・(9)
・・・・・(9)
図7は,図6の回路のシミュレーション結果です.1kHzでのゲインは56dBとなっており,ほぼ計算通りのゲインとなっていることがわかります.
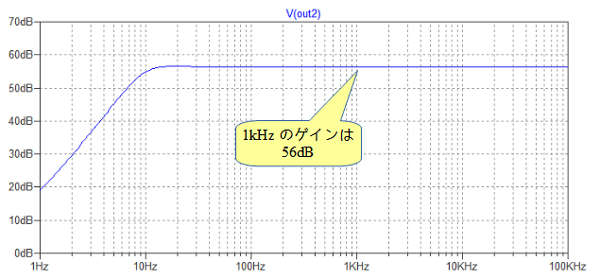
1kHzでのゲインは56dBでほぼ計算通り.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice2_023.zip
●データ・ファイル内容
CE_amp_EF.asc:図3の回路
2stage_amp_2out.asc:図4の回路
2stage_amp_HiG.asc:図6の回路
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs
(5) LTspiceアナログ電子回路入門・アーカイブs










