同相ノイズの混入が少ない差動アンプはどっち？

■問題

小川　敦　Atsushi Ogawa

　図1の回路（a）と（b）は差動増幅回路です．差動増幅回路は，生体信号のような大きなノイズの中から小さな信号を取り出す用途などに使われています．回路（a）は，スイッチト・キャパシタを使った差動増幅回路です．SW₁とSW₂は，10kHzのクロック信号で制御されています．回路（b）は，一般的な差動増幅回路です．回路（a）と（b）の抵抗R₂は，共に抵抗精度の関係で設計値の20kΩに対して，20.2kΩと1%大きくなっています．
　この回路（a）と（b）に，小さな差動信号（20Hz，0.4mV_PP）と大きな同相ノイズ（50Hz，0.4V_PP）を重畳（ちょうじょう）し入力しました．この場合，出力において50Hzの同相ノイズの混入が少ないのは回路（a）と（b）のどちらでしょうか．

図1　問題の差動増幅回路（a）と（b）
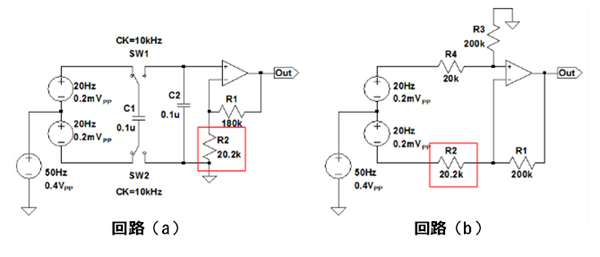
どちらも抵抗R₂が設計値よりも1%大きくなっている．

■解答

回路（a）
　回路（a）は，スイッチト・キャパシタにより，まず，C₁で同相ノイズを取り除き，その同相ノイズを取り除いた信号をC₂に充電します．充電されたC₂の信号は，R₁とR₂による非反転アンプで，GND基準のシングル信号として増幅されます．そのため，R₂に抵抗誤差があっても，ゲインが変わるだけで同相ノイズの混入量が増えることはありません．回路（b）は抵抗（R₂）に誤差があると，同相除去比が悪化してしまうため，出力の同相ノイズが増えてしまいます．したがって，50Hzの同相ノイズの混入が少ないのは，回路（a）になります．

■解説

●差動増幅回路の同相除去比が重要
　差動増幅回路の性能を表す指標の一つに同相除去比（式1）があります．

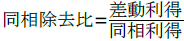・・・・・・・・・・・・・・・・・・・・・・・・・・・・・（1）

　同相除去比は，大きいほど同相ノイズの影響を受けにくくなります．特に大きな同相除去比が必要となる例として，生体信号の取り出しなどの用途があります．
　生体信号（脳波や筋電，心電など）を計測しようとすると，信号自体が非常に微弱なうえ，商用電源からのノイズ（ハム・ノイズ）が大きなレベルで重畳していることが問題となります．そこで，2カ所から信号を取り出し，差動増幅回路を使用して，二つの信号に共通して重畳しているハム・ノイズを打ちすようにして計測します．ところが，同相ノイズとして重畳するハム・ノイズのレベルが信号の1000倍以上も大きいことがあるため，同相除去比の良くない差動増幅回路を使用すると，ハム・ノイズが十分に打ち消されず，最終出力に混入してしまいます．そのため，このような用途に使用する差動増幅回路は，同相除去比が非常に重要になります．

●一般的な差動増幅回路の同相除去比
　最初に回路（b）の同相除去比について解説します．回路（b）の差動利得は式2で，同相利得は式3で，さらに同相除去比は式4で表されます．

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

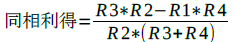・・・・・・・・・・・・・・・・・・・・・・・・・・(3)

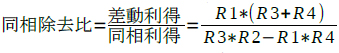・・・・・・・・・・・・・・・・・・・(4)

　式3，式4で「R₃*R₂＝R₁*R₄」であれば，同相利得は0となり，同相除去比は無限大になります．ところが，抵抗値に誤差があると，同相除去比はすぐに悪化してしまいます．図1の回路（b）の定数で計算してみると式5のように，61dB程度となってしまいます．

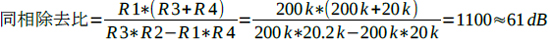・・・・・(5)

　そこで，回路（b）の入力信号の条件で，同相成分がどのくらい出力に混入するか計算してみます．同相利得は式3に定数を代入することで計算できます．しかし，ここでは，差動利得と同相除去比から同相利得を求められるように計算します．（一般的に機器のカタログなどには，差動利得と同相除去比しか掲載されてない場合が多いと思われるため）式4を変形すると，同相利得は式6になります．

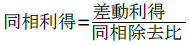・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6）

　回路（b）のR₁が200kで，R₂が20.2kなので，差動利得は式2より約20dBとなります．同相除去比は式5より約61dBです．式6を使用して同相利得を求めますが，dB計算では，割り算は引き算に変換されます．なので，同相利得は「20dB-61dB」で-41dB(1/110倍）となります．そのため出力には，同相ノイズが3.6mV_PP（0.4V_PP*1/110）出力され，差動信号の4mV_PPとほぼ同じレベルのノイズが混入することになります．

●スイッチト・キャパシタを使った差動増幅回路の動作
　次に，回路（a）のスイッチト・キャパシタを使った差動増幅回路について解説します．図2は回路（a）の動作を説明するための回路図です．SW₁とSW₂は，T1の状態とT2の状態を10kHzで周期的に繰り返しています．
　まず，T1の状態のとき，SW₁とSW₂は左側がONとなり，C₁には差動信号（Vd）により，「2*Vd」の電圧が充電されます．このとき重要なのが，C₁の充電電圧は，「Vc+Vd-(Vc-Vd)＝2*Vd」より，同相ノイズ（Vc）の値に影響を受けない，ということです．
　T2の状態のとき，SW₁とSW₂は右側がONとなり，T1でC₁に蓄えられた電荷はC₂に分配されます．C₁とC₂の容量値（0.1μF）は同じなので，この時点では，C₂の電圧は半分の「Vd」になります．
　次の周期のT1で，再度C₁に「2*Vd」が充電されたとき，次の周期のT2で，C₂は「1.5*Vd」の電圧まで充電されます．この動作を繰り返すことで，C₂の電圧は「2*Vd」まで充電されることになります．
　OPアンプは，R₁とR₂により，非反転アンプとして動作し，C₂の電圧をGND基準で増幅します．そのゲインは式7になり，これが回路（a）の差動利得となります．

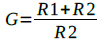・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(7)

　回路（a）でR₁とR₂に誤差が発生したとしても利得が多少変わるだけです．T1で信号をC₁に充電する時点で，同相ノイズの影響が排除されているため，抵抗誤差があっても同相除去比は悪化しません．

図2　図1回路（a）の動作を説明するための回路図
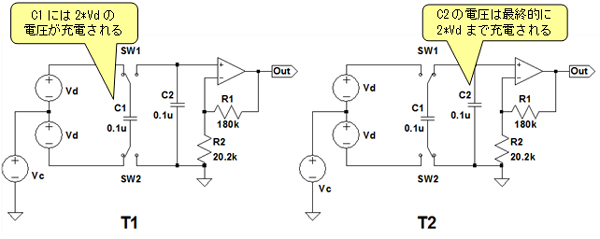
SW₁とSW₂はT1とT2の状態を10kHzで周期的に繰り返す．

●回路（a）に直流電圧を入力してどのようにコンデンサに充電されるかを確認する
　図3は，回路（a）でC₂が充電される様子を確認するために，直流電圧を入力するシミュレーション回路です．差動信号（Vdp，Vdm）は，共に0.2mVの直流電圧で，両端電圧が0.4mVとなります．同相電圧（Vc）は，0.4Vの直流電圧としています．図2のSW₁とSW₂は，SW₁が「S₁とS₄」，SW₂が「S₂とS₃」の電圧制御スイッチの組み合わせとなっています．それぞれのスイッチは，同時にハイレベルとならないように，10kHzのクロック信号CK₁とCK₂でコントロールされています．CK₁がハイレベルのときS₁とS₂がオンし，CK₂がハイレベルのときS₃とS₄がオンします．また，C₂の充電電圧の初期値を0Vとするため，「.IC」コマンド(Set Initial Conditions）を追加しています．「.Ic V(VC₂)＝0」とすることで，VC₂端子の電圧（C₂の充電電圧）の初期値を0Vにセットしています．

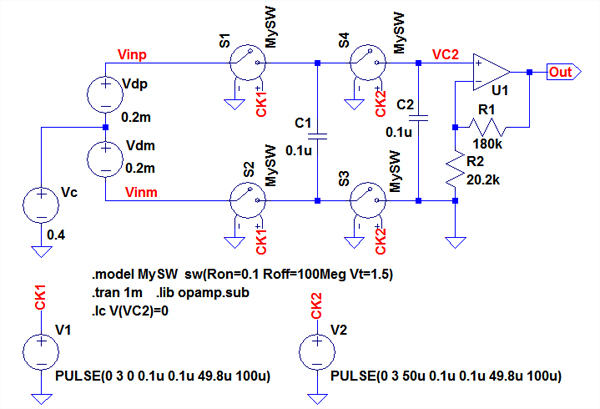
図3　図1回路（a）でC₂が充電される様子をシミュレーションするための回路
入力両端電圧は0.4mV，同相電圧は0.4Vの直流電圧．

　図4が図3のシミュレーション結果です．下段がCK₂の電圧で，上段がVC₂端子の電圧（C₂の電圧）です．VC₂端子の電圧が徐々に上昇し，最終的には入力両端電圧と同じ400μV(0.4mV)になることが分かります．

図4　図3のシミュレーション結果
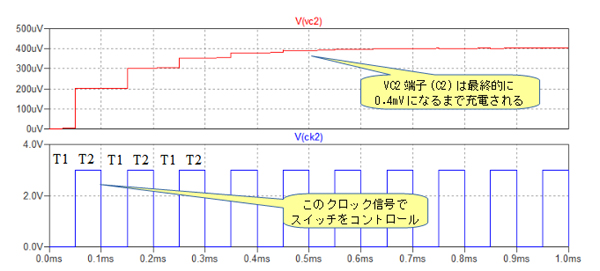
C₂は徐々に充電されていき，最終的には入力両端電圧と同じ0.4mVになる．

●回路（a）に交流信号を入力してノイズ除去を確認する
図5は，図1の回路（a）の動作をシミュレーションするための回路です．差動信号（Vdp，Vdm）は，共に0.2mVで20Hzの正弦波です．両端電圧としては0.4mV_PPの正弦波になります．同相ノイズ（Vc）の電圧は0.4V_PPで，50Hzの正弦波です．

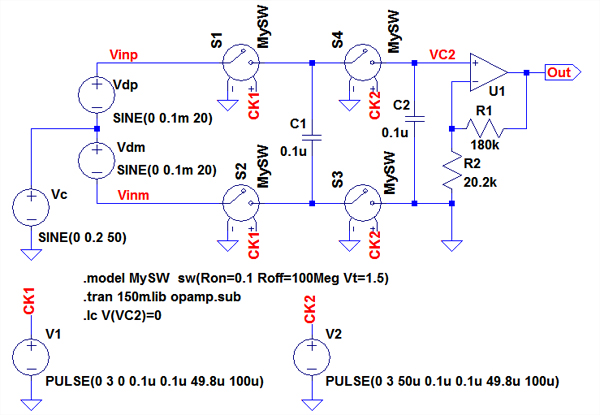
図5　図1回路（a）の動作をシミュレーションするための回路
差動入力信号は0.4mV_PPで20Hzの正弦波．同相ノイズは0.4V_PPで50Hzの正弦波．

　図6は，図5のシミュレーション結果です．下段が入力端子の片側（Vinp端子）の電圧で，上段がOPアンプ出力（Out端子)の電圧です．下段のVinp端子では，差動信号が小さすぎるため，50Hzの同相ノイズしか確認することができません．しかし，OPアンプ出力にはその同相ノイズは全く無く，20Hzの差動信号のみが10倍に増幅され4mV_PPの信号として出力されていることが分かります．
　このように，回路（a）は同相除去比が非常に優れています．しかし，スイッチト・キャパシタを使用しているため，クロック周波数の1/2よりも充分低い周波数の信号しか扱えないので注意が必要です．

図6　図5のシミュレーション結果
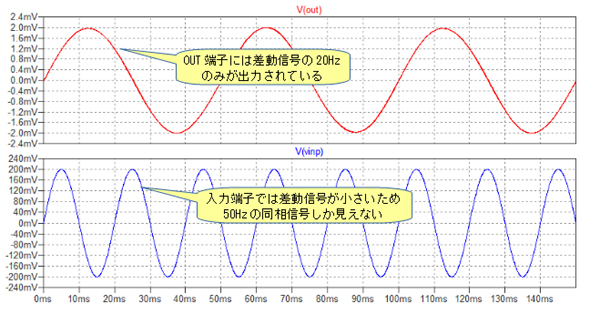
OUT端子には差動信号の20Hz成分のみが出力されている

●回路（b）の交流信号での動作シミュレーション
　図7は，図1の回路（b）のシミュレーション用の回路図です．入力信号は図5と同じで，差動信号（Vdp，Vdm）は，共に0.2mVで20Hzの正弦波です．両端電圧としては0.4mV_PPの正弦波になります．同相ノイズ（Vc）の電圧は0.4V_PPで，50Hzの正弦波になっています．

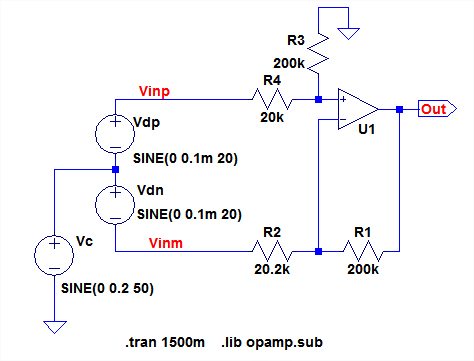
図7　図1回路（b）のシミュレーション用の回路図
差動入力信号は0.4mV_PPで20Hzの正弦波．同相ノイズは0.4V_PPで50Hzの正弦波．

　図8がそのシミュレーション結果です．下段は入力端子の片側（Vinp端子）の電圧で，図6のシミュレーション結果と同じです．しかし，上段のOPアンプ出力（Out端子)の電圧波形は，図6とは異なり，差動信号の20Hz成分に，同相ノイズの50Hz成分が混入しているのが分かります．このシミュレーション結果からも，回路（b）は大きな同相除去比が必要な用途には向いていないことが分かります．

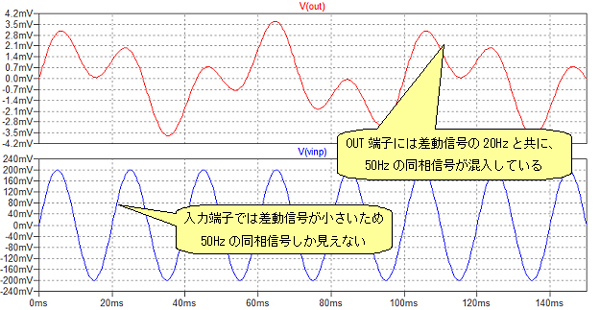
図8　図7のシミュレーション結果　
OUT端子には差動信号の20Hz成分と共に，同相信号の50Hz成分がかなり多い．

　最後に，回路（a）の考え方を使用して，使い易く設計されたICが存在しますので紹介します．抵抗で利得をプログラム可能な，高精度レール・トゥ・レール入出力ゼロ・ドリフト計装アンプ「LTC2053」です．このICはLTspiceのライブラリにも登録されており，Componentライブラリから呼び出してシミュレーションすることが可能です．参考までに，LTC2053を使用して，図5と同等なシミュレーションを行う回路図をデータ・ファイルに収録してあります．

■データ・ファイル

解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice046.zip

●データ・ファイル内容
SC_Diff_Amp_DC.asc：図3回路
SC_Diff_Amp_SINE.asc：図5回路
Diff_Amp_B.asc：図7回路
2053.asc:LTC2053を使用した回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください