正しく周波数変換とスケーリングした回路はどっち?

図1の回路(a)と(b)は,図1上段左の遮断周波数(ωC)が1rad/sである「Sallen-Key 2次バターワース・ローパス・フィルタ(LPF)」を,図1上段右の「Sallen-Key 2次バターワース・ハイパス・フィルタ(HPF)」へ周波数変換し,遮断周波数(fC)を1kHzとするため,全てのコンデンサを0.01μFへ変更し,抵抗をスケーリングした回路です.
回路(a)と(b)の違いは,回路(a)の「R1a,R2a」と回路(b)の「R1b,R2b」の定数が入れ替わっています.この場合,遮断周波数(fC)が1kHzのSallen-Key 2次バターワースHPF回路は,回路(a)と(b)のどちらでしょうか.
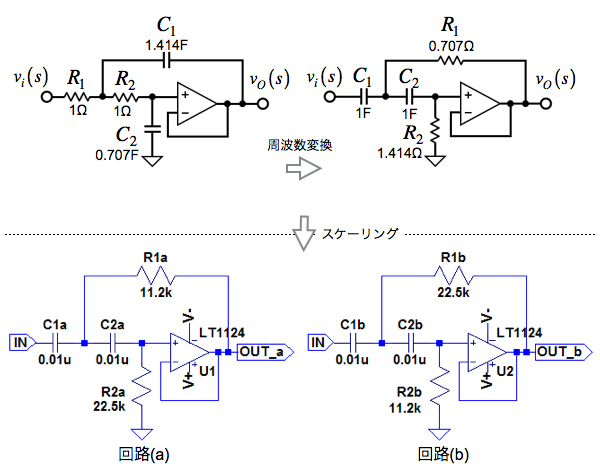
図1 上段左は,遮断周波数(ωC)を1rad/sに正規化したSallen-Key 2次バターワースLPF
図1 上段右は,上段左を周波数変換した,Sallen-Key 2次バターワースHPF
回路(a)
今回は,正規化されたLPF回路を周波数変換でHPF回路へ変換し,現実的な回路にするためのスケーリングする手順を解説します.図1上段のLPF回路をHPF回路に変換するには,まず周波数変換を行います.周波数変換は,抵抗をコンデンサに置き換え,その値を「1/R」にします.また,コンデンサは,抵抗に置き換え,その値を「1/C」にします.具体的に,抵抗は,上段左のR1とR2を上段右のC1とC2にして値が「1/1=1F」となります.コンデンサは,上段左のC1を上段右のR1にして値が「1/1.414=0.707Ω」となります.同様にC2をR2にして値は「1/0.707=1.414Ω」となります.
次に,周波数変換をした回路をスケーリングし,バターワース特性を保つには,上段右の「R1=0.707Ω」と上段右の「R2=1.414Ω」の比を保たなければなりません.そこで,この比になっているのは,回路(a)となります.
●フィルタはLPFが基本
フィルタは,正規化されたLPFが基本となります.そのLPFを周波数変換して,HPFやバンドパス・フィルタ(BPF),バンド・エリミネーション・フィルタ(BEF)など,別のフィルタ回路を作ります.今回は,同じ遮断周波数(ωC=1rad/s)のSallen-Key HPF回路を作成し,現実的な回路にするため,全てのコンデンサを0.01μFで遮断周波数(fC)が1kHzとなるようにスケーリングを行います.
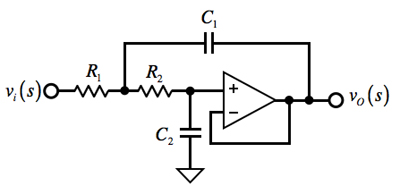
図2は,図1上段左と同じ基本的なSallen-Key 2次LPF回路です.Sallen-Keyとは,二人の開発者R.P.SallenとE.L.Keyの名がついています.また,回路の方式からVCVS法とも言われます.VCVS(Voltage Control Voltage Source)は,電圧制御電圧源であり,図2ではオペアンプのボルテージ・ホロワ回路(ゲイン=1)を指します.Sallen-Key 2次LPFは,受動部品が4個で,部品点数が少ないことからよく使用される回路です.
●LPF回路のC1とC2の定数を導き出す
まず,図1上段左のC1とC2の定数を導き出すため,Sallen-Key 2次LPF回路の伝達関数と一般式から,回路の「ゲイン(H)」や「遮断周波数(ωC)」,「Q(Quality Factor)」と四つの受動素子の関係を調べます.
Sallen-Key LPF回路の伝達関数は,式1で表されます.
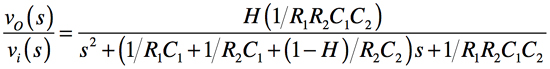 ・・・・・(1)
・・・・・(1)
ここで,回路のゲインは,ボルテージ・ホロワ回路ですので「H=1」であること,また二つの抵抗(R1,R2)を単位値である「1Ω」とすれば,式2となります.
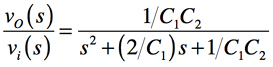 ・・・・・・・・・・・・・・・・・・・・・・・・(2)
・・・・・・・・・・・・・・・・・・・・・・・・(2)
2次LPF伝達関数の一般式はゲインや遮断周波数,Qを用いて表すと式3になります.
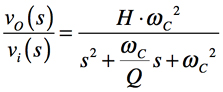 ・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・(3)
「式2=式3」となるので,C1とC2の定数を導き出すのは,2次LPF伝達関数の一般式(式3)で示されるωCおよびQに関係する項と,式2の項を比較すれば容易に求められます.式3において,ゲインを「H=1」,遮断周波数を「ωC=1rad/s」として,式2と比較すると,「ωC2=1/C1C2=1」より「C1C2=1」です.
また,式2分母の「2/C1」と式3分母の「ωC/Q」がイコールとなり,「ωC=1」より「C1=2Q,C2=1/2Q」の関係であることがわかります.この関係を図1上段左にあてはめます.バターワース特性のQは「Q=0.707」ですので,「C1=2Q=1.414F」,「C2=1/2Q=0.707F」となります.
●LPFからHPFへの周波数変換
図3(a)と(b)は,LPFとHPFの周波数特性を示しまた.LPFと同じ特性(ここではバターワース特性)を持ったHPFは,その周波数特性が逆となります.この逆の関係を用いて,LPFからHPFへ回路を変換することができます.具体的な変換は,LPFの伝達関数中の「s」を「1/s」と変換することで得られます.これを周波数変換と呼びます.この変換により,アクティブ・フィルタ(ここではSallen-Key LPF)の受動素子は,図4のように抵抗をコンデンサに置き換え,その値を「1/R」とします.また,コンデンサは抵抗に置き換え,その値を「1/C」とします.
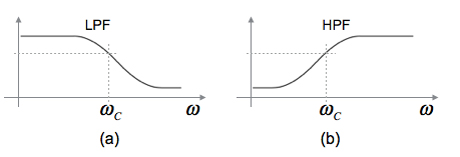
周波数特性は逆になります.
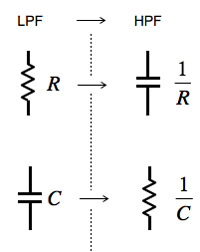
抵抗はコンデンサに置き換え値を「1/R」,コンデンサは抵抗に置き換え値を「1/C」.
●LPFとHPFの周波数特性をLTspiceで確認する
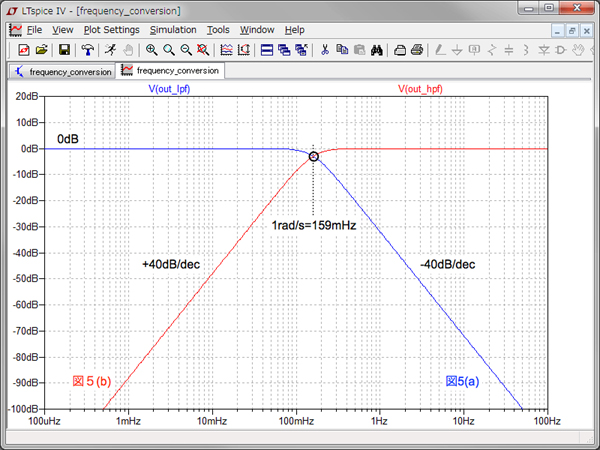
図5(a)は,図1上段左のLPFと,図5(b)が図1上段右のHPFの特性をシミュレーションする回路です.図5(a)は,遮断周波数(ωC)が1rad/sで,抵抗(R1c,R2c)が1ΩのSallen-Key LPF回路で,コンデンサは前述で求めた値(C1c=2Q,C2c=1/2Q)です.
図5(b)は,図5(a)をHPF回路へ周波数変換した回路となります.また図5(a)と(b)のQは,バターワース特性「Q=1/√2=0.707」を与え,OPアンプは理想としました.
図5(a)のLPFの受動素子をHPFへ周波数変換すると次のようになり,図5(b)の受動素子へ変換できます.
C2c=0.707F → R2d=1/0.707=1.414Ω
R1c=1Ω → C1d=1/1=1F
R2c=1Ω → C2d=1/1=1F
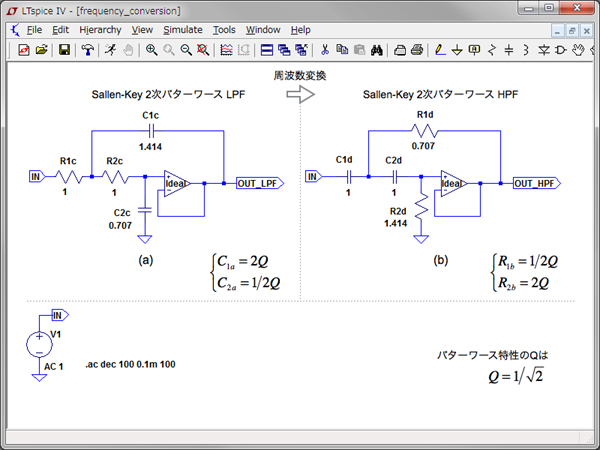
(b)は(a)を周波数変化した回路.
図6は,図5(a)と(b)のシミュレーション結果です.シミュレーション結果の図5(a)は,2次バターワースLPFの特性になっています.特性は,通過域では0dBで減衰せず平坦で,遮断周波数(ωC=1rad/s)では-3.01dB減衰し,遮断周波数(ωC)より高い周波数では-40dB/decの減衰となっています.シミュレーション結果の図5(b)は,図5(a)とは逆になり,HPFへ変換されているのがわかります.
●現実的な回路にするためのスケーリング
次に,周波数変換した図5(b)の回路を使い,現実的な回路にするためにスケーリングを行います.図7は,図5(b)の回路をスケーリングした,図1の回路(a)と(b)をシミュレーションする回路です.
問題の条件である,遮断周波数(fC)を1kHz,全てのコンデンサを0.01μFとして,抵抗をスケーリングします.まず,遮断周波数(fC)を1kHzとする周波数のスケーリング係数(kf)は,「kf=2π(1000)」となります.また,全てのコンデンサを0.01μFとするインピーダンス・スケーリング係数(km)は,「km=1/(0.01×10-6×kf)=15.9×103」で求められます.これより,図7のコンデンサ(C1a,C2a,C1d,C2d)は,0.01μFになります.
次に,図5(b)の抵抗(R1d,R2d)をスケーリングすると,図7(a)のように,R1aは,「0.707Ω×15.9×103」より11.2kΩとなります.R2aは,「1.414Ω×15.9×103」より22.5kΩになります.
図7(b)の抵抗「R1b,R2b」は,「R1a,R2a」の定数を入れ替えています.また,図7(a)と(b)のOPアンプは,より現実的な回路に近づけるために,マクロモデル(LT1124)を使用しています.
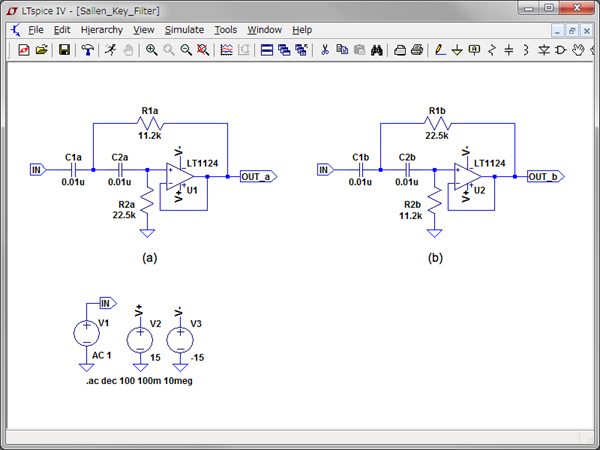
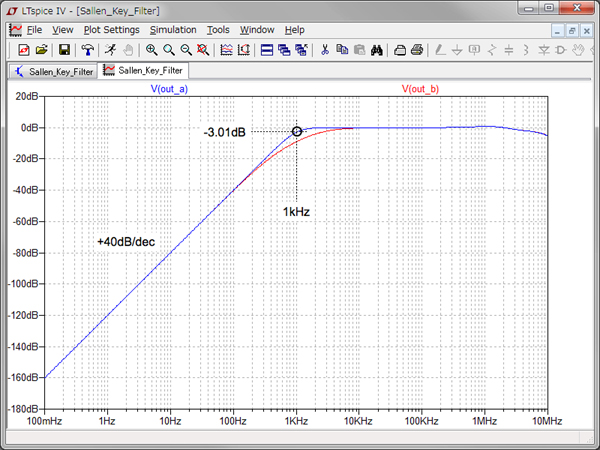
図8は,図7のシミュレーション結果です.正しく周波数変換とスケーリングした回路(a)は,バターワース特性を持った2次 Sallen-Key HPFであることがわかります.一方,抵抗の定数を入れ替えた回路(b)は,バターワース特性になっていません.
●量産する場合は特性の変動を考慮
最後に今回のように作ったフィルタは,受動部品の許容誤差により特性が変動します.チャンピオン品のような1台しかないフィルタは,受動素子を選別して目的の特性に合わせることもできます.しかし,同じ回路を量産する場合は特性の変動を考慮しなければなりません.
本メルマガの10回目に配信した「ばらつきが少ない回路はどっち?」はモンテカルロ・シミュレーションを使い,3次 Sallen-Key LPFの受動部品の許容誤差によりフィルタの特性がどのように変わるか調べる記事です.仕様を満足するフィルタ回路が出来上がった後は,モンテカルロ・シミュレーションで回路の特性変動を調べることも重要です.
解説に使用しました,LTspiceの回路をダウンロードできます.
LTspice039.zip
●データ・ファイル内容
Ideal_OP.asy:図5のOPアンプ・シンボル
Ideal_OP.asc:図5のOPアンプ回路
frequency_conversion.asc:図5の回路
Sallen_Key_Filter.asc:図7の回路
※ファイルは同じフォルダに保存して,フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
(4) LTspice電子回路マラソン・アーカイブs










