ばらつきが少ない回路はどっち？
図1の回路（a）と回路（b）は，カットオフ周波数1kHzの3次Sallen-Keyローパス・フィルタ回路です．回路（a）と回路（b）それぞれのOPアンプは理想とし，抵抗はE24系列（R1=11kΩ，R2=110kΩ，R3=33kΩ）として，コンデンサはE6系列（C1=0.015μF，C2=0.001μF，C3=0.0068μF）としました．
回路（a）は，抵抗とコンデンサの分布が，一様分布（Uniform分布）で，回路（b）の抵抗とコンデンサの分布は，正規分布（Gauss分布）とします．
このように，部品の分布に違いがある回路（a）と回路（b）をモンテカルロ解析を行った場合，カットオフ周波数の分布が狭い（ばらつきが少ない）回路はどちらでしょうか？
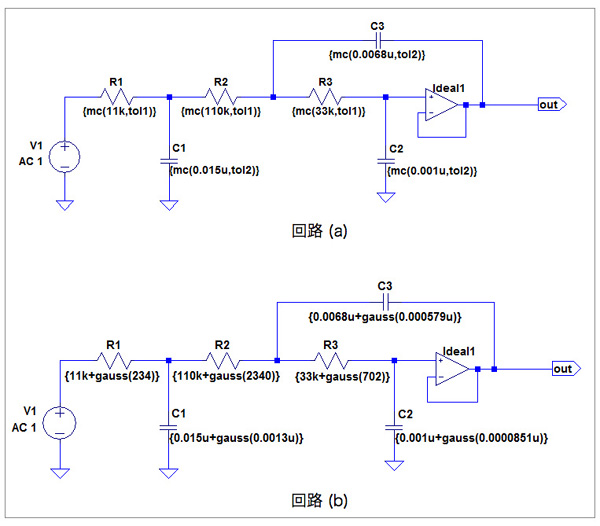
抵抗とコンデンサの分布が，回路（a）は一様分布（Uniform分布）で，回路（b）は正規分布
●一様分布と正規分布
回路（a）の一様分布[図2(a)]の抵抗とコンデンサの値は，その素子値と許容誤差を入れます．具体的には，E24系列なら素子の値±5%の許容誤差から0.05，E6系列なら素子の値±20%の許容誤差から0.2を入れています．
回路（b）の正規分布[図2(b)]の抵抗とコンデンサの値は，その素子値と正規分布の標準偏差（σ）を入れます．本来の標準偏差は，部品のバラツキを調べて，回路図へ入れますが，今回はそのデータがありません．そこで，系列のバラツキの半分を半値全幅（Full Width at Half Maximum：FWHM）と仮定し，式1から求めたσで代用します．具体的には，E24系列なら素子の値±5%の半分の±2.5%を半値全幅として，E6系列なら素子の値±20%の半分の±10％分を半値全幅とします.
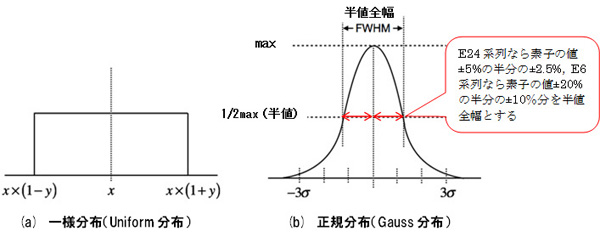
一様分布の値は素子値と許容誤差．正規分布の値は素子値と正規分布の標準偏差（σ）
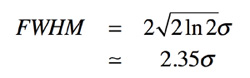・・・・・・・・・・・・・・・・・・・・・・・・(1)
回路（b）
一様分布はその許容誤差内で均一となります．正規分布は，平均値を中心とした山の形です．Sallen-Key ローパス・フィルタのカットオフ周波数は抵抗とコンデンサの値により決まります．抵抗とコンデンサの許容誤差内の最悪値は，正規分布よりも一様分布のほうが多くあるため，カットオフ周波数の分布は正規分布の方が狭く，ばらつきが少なくなります．
●モンテカルロ解析とは
SPICEのモンテカルロ解析は，製品の量産時に，回路を構成している部品の値を許容誤差の分布と乱数でばらつかせて，数多くのシミュレーションを繰り返すことにより，回路の応答がどのように変化するかを調べます．
今回は，LTspiceに実装されている一様分布関数と正規分布関数を使用し，3次Sallen-Keyローパス・フィルタ（抵抗はE24系列，コンデンサはE6系列）のカットオフ周波数のばらつきを比較します．
●LTspiceの統計で使う関数について
LTspiceは，統計で使う関数があらかじめ登録されています．回路部品の誤差による特性の検証は，一様分布の「mc関数」と正規分布の「gauss関数」を使います．文法は次のようになります．
mc(x,y) ：x*(1+y)値 から x*(1-y) 値間で一様分布の乱数を発生
gauss(x) ：標準偏差（σ），今回は標準偏差x値から正規分布の乱数を発生
この関数を用いた素子を回路部品として，その素子値を許容誤差の分布内で変化させ，複数回シミュレーションを実行して出力応答の分布を調べます．1回のシミュレーションで各々の関数から得られる乱数は1つです．仮にN=100の母数で値の変化を確かめたいときは100回シミュレーションを実行します．LTspiceには「.stepコマンド」がありますので，ダミーの変数を与えて，シミュレーションを100回繰り返すという処理で実現します．
LTspiceに登録されている関数の一覧はHELPの目次から，「LTspice®IV → LTspice® → Dot Commands → .param -- User-Defined Parameters」で確認できます．
●一様分布と正規分布を確かめる
一様分布の1kΩの抵抗を測定する回路は図3で，正規分布の1kΩの抵抗を測定する回路は図4です．一つの回路には，同じ値の抵抗が3本あり1Aの電流で生じた電圧降下を抵抗値として読んでいます．3本用意したのは1回のシミュレーションによる乱数発生で各抵抗値へ違った誤差が与えられるかを確かめるためです．抵抗値は波括弧でくくった変数とし，一様分布・正規分布は下記のように与えています．
一様分布：{mc(1k,tol)} 1kΩ±100Ω tol=0.1とし±100Ωとする
正規分布：{1k+gauss(42.6)} 標準偏差 42.6Ω 半値全幅のσを利用
σ=半値全幅/2.35の関係を用い，σ=100Ω/2.35=42.6Ωを利用
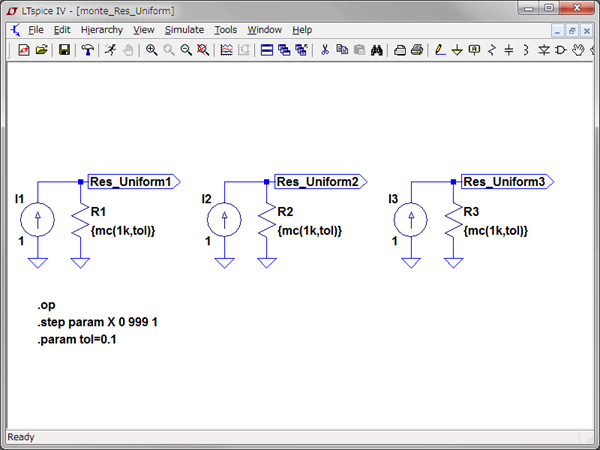
一つの回路には，同じ値の抵抗が3本ある
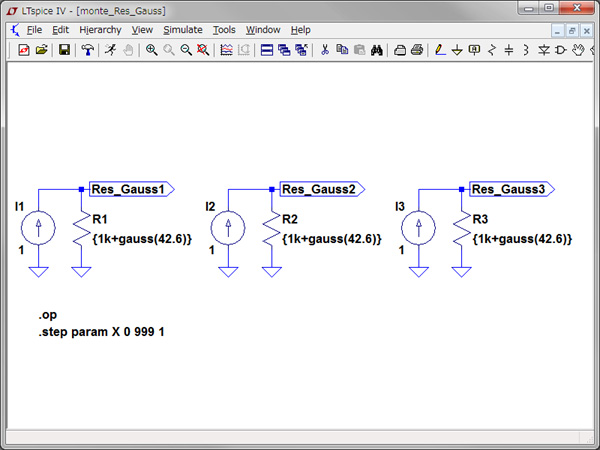
一つの回路には，同じ値の抵抗が3本ある
本来正規分布の標準偏差は，測定値から出します．ここでは，抵抗の許容誤差±100Ωから半値全幅（FWHM）=100Ωとし，正規分布と半値全幅（FWHM）の関係から求める標準偏差で代用しました．式1が半値全幅（FWHM）と標準偏差(σ)の関係式です．
分布の形が見えやすいように1000回繰り返すシミュレーションとし，Xというダミーの変数を 0から999までステップ1で繰り返します．メニューバーで「Edit > SPICE Directive」，またはショートカットキーの「S」を使い，次の「.step」コマンドを入力します．
.step param X 0 999 1
図5が一様分布，図6が正規分布のシミュレーション結果です．図5と図6の横軸は，シミュレーションの回数であり3本の抵抗は1回のシミュレーションで各々異なる誤差になっています．
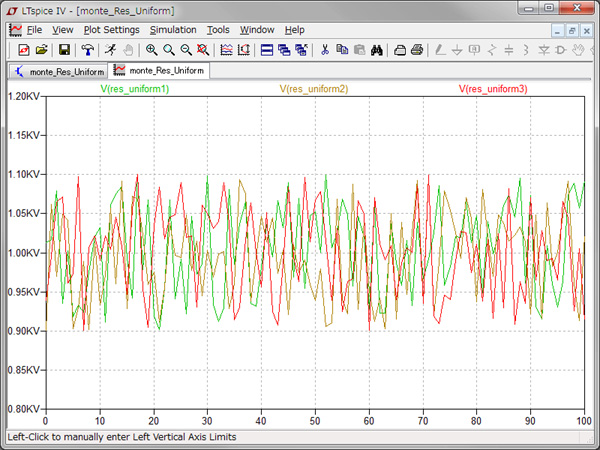
横軸は，シミュレーションの回数
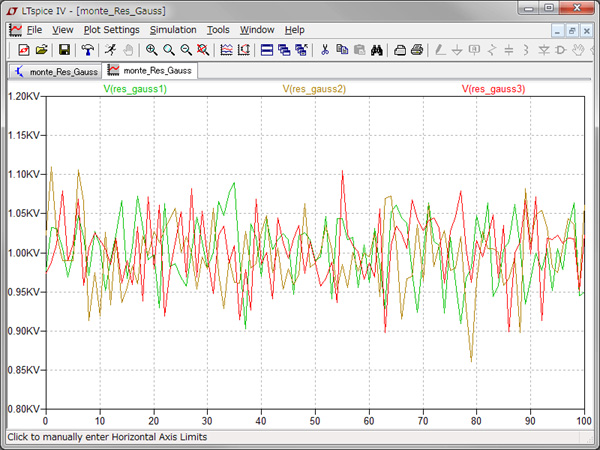
横軸は，シミュレーションの回数
また，シミュレーションした3本の抵抗をヒストグラムにしました．図7が一様分布で，図8が正規分布となります．図7と図8のヒストグラムより，一様分布は許容誤差±100Ωの間で均一の分布になり，正規分布は標準偏差42.6Ωで山の形になることが分かります．部品の誤差がどのような分布なのかを調べて，一様分布と正規分布を使い分けてシミュレーションすることが大切です．
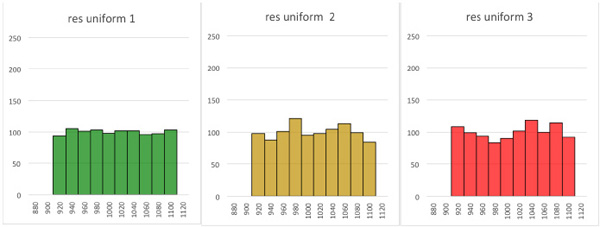
一様分布は許容誤差±100Ωの間で均一の分布
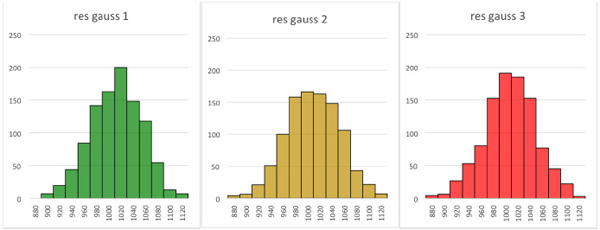
正規分布は標準偏差42.6Ωで山の形になる
●3次Sallen-Keyローパス・フィルタのカットオフ周波数の分布を調べる
まず，カットオフ周波数（利得が-3dB周波数）が1kHzの3次Sallen-Keyローパス・フィルタを構成します．抵抗はE24系列，コンデンサはE6系列から選びます．この場合の，カットオフ周波数の分布をモンテカルロ解析で調べてみましょう．各部品の誤差はその系列からくるものを与え，E24系列は±5%，E6系列は±20%とします．
図9と図10がシミュレーションする3次Sallen-Keyローパス・フィルタ回路です．抵抗とコンデンサは，図9が一様分布で，図10が正規分布の指定です．一様分布はtol1,tol2へ系列の許容誤差を代入します．正規分布のσは，E24系列の誤差±5％の±2.5%分，E6系列の誤差±20%の±10%分が半値全幅になる標準偏差を式1から求めて与えました．受動部品のパーツリストを表1へ示します．オペアンプの直流利得は，100dBの理想オペアンプを使用します．求めたいカットオフ周波数は低周波1Hz時の利得から-3dB下がる周波数を「.MEAS」コマンドで計算させます．
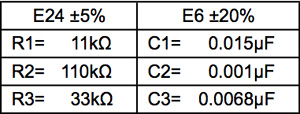
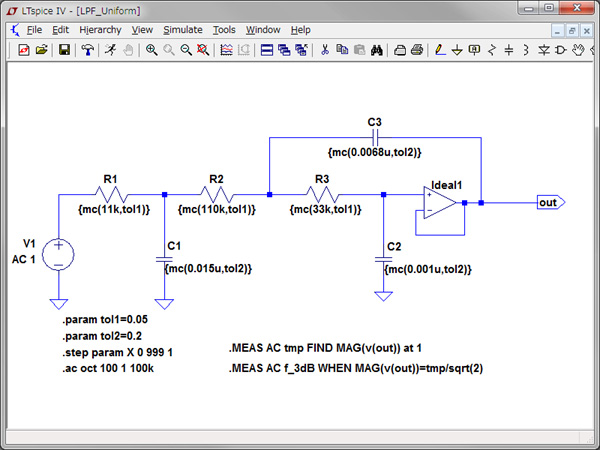
カットオフ周波数は1kHz，利得は-3dB周波数
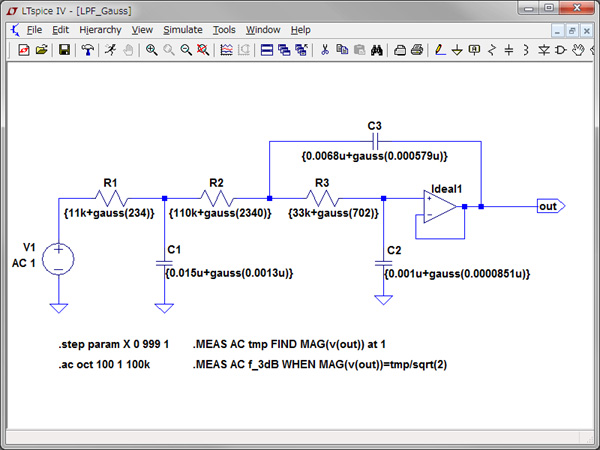
●「.MEAS」コマンドを確認する
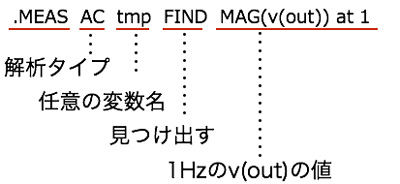
1Hz時のOUT端子の電圧を探すFINDはLTspiceの文法から「.MEAS AC tmp FIND MAG(v(out)) at 1」となり，内容は，「AC解析において，1Hz時のOUT端子の電圧を探して変数tmpへ入れなさい」となります．
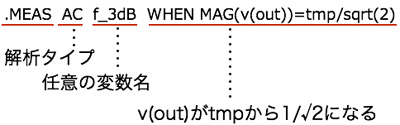
OUT端子がtmpから1/√2（-3dB）になる周波数を探すWHENはLTspiceの文法から「.MEAS AC f_3dB WHEN MAG(v(out))=tmp/sqrt(2)」となり，内容は，「AC解析において，変数tmpから1/√2となる周波数をf_3dBへ入れなさい」となります．
ログ・ファイルを見るときはメニューバーの「View > SPICE Error Log」または，ショートカット・キーの「Ctrl+L」でログ・ファルのウィンドが現れます．シミュレーション実行後のログ・ファイルにはカットオフ周波数が次のように出力されました．ここではstep 5までを載せています．
step mag(v(out))=tmp/sqrt(2)
1 961.187
2 1038.57
3 1191.81
4 1147.8
5 991.569
続く
●カットオフ周波数の分布を比較
図11と図12は，図9と図10のOUT端子の周波数特性のシミュレーション結果です．図13が「.meas」コマンドで記録されたログファイルから作成したカットオフ周波数（-3dB周波数）のヒストグラムです．カットオフ周波数の分布の広がりは正規分布の方が狭くなることがわかります．
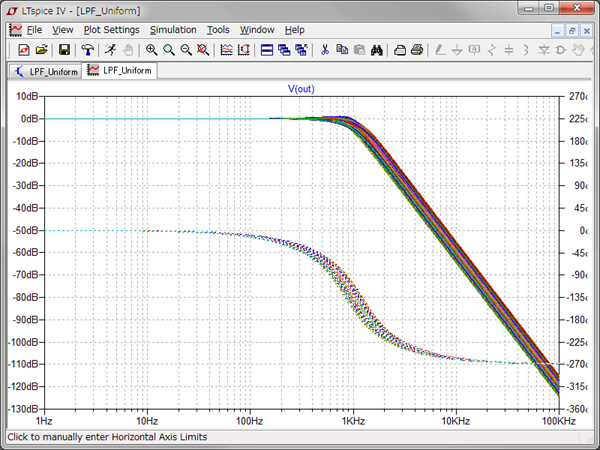
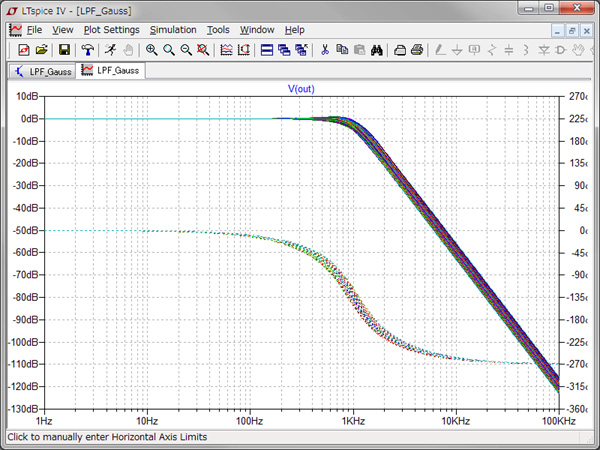
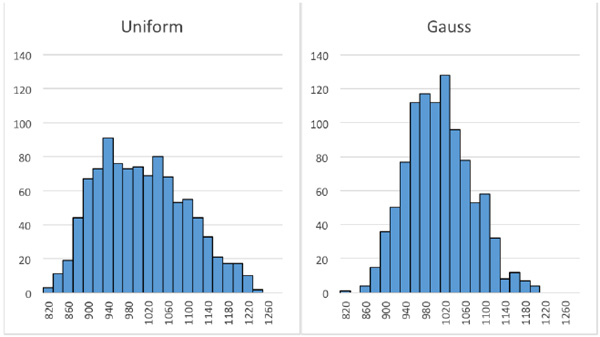
カットオフ周波数の分布の広がりは正規分布の方が狭くなることがわかる
このように回路を構成する部品の許容誤差を与えて，モンテカルロ解析を行えば測定したい端子の変動がわかります．チャンピオン品のような一つだけ良いものを作るのではなく，長期にわたって作り続けた場合の分布が予測できますので有益な解析となります．部品の最悪値を回路へ与え重箱の隅をつつくような検証方法もあります．しかしその方法は測定したい端子がどのような分布になるかは分かりません．各部品の誤差を人の手で組み合わせて検証するのは気が遠くなります．このようなときこそEDAツールの出番であり，シミュレータによる設計支援を上手に利用したいものです．解析に時間がかかるモンテカルロ解析ですが，やって損は無い検証の一つです．
解説に使用しました，LTspiceの回路をダウンロードできます．
LTspice010.zip
●データ・ファイル内容
Ideal_OP1.asc：理想OPアンプの回路
Ideal_OP1.asy：理想OPアンプのシンボル
monte_Res_Uniform.asc：図3の回路
monte_Res_Gauss.asc：図4の回路
LPF_Uniform.asc：図9の回路
LPF_Gauss.asc：図10の回路
※ファイルは同じフォルダに保存して，フォルダ名を半角英数にしてください
■LTspice関連リンク先
(1) LTspice ダウンロード先
(2) LTspice Users Club
(3) トランジスタ技術公式サイト LTspiceの部屋はこちら
